
Джон Норт
Космос. Иллюстрированная история астрономии и космологии
КОСМОЛОГИЧЕСКИЕ ВОЗЗРЕНИЯ В VI В. ДО Н. Э
Аристотель – величайший античный философ IV в. до н. э. – основал традицию обобщенного изложения мнений предыдущих мыслителей в целях их критического переосмысления в столь полемичной манере, как будто бы он спорил с еще живыми людьми. Некоторые упоминаемые им факты восходят к VI в. до н. э., однако как и многие из тех, кто интересовался ранними учениями, он в значительной степени зависел от посредников, которые не всегда были точны. Это особенно справедливо в отношении четырех наиболее древних упоминаемых им философов-мыслителей – Фалеса, Анаксимандра, Анаксимена и Пифагора, живших в VI в. до н. э. Аристотель считал Фалеса основателем ионийской традиции натуральной философии – знания о физическом мире. Ходили слухи о чрезвычайной практической сметке Фалеса – например, о том, как он, использовав свои астрономические познания, сумел предсказать обильный урожай оливок. Монопольно арендовав все маслодавильни, он неслыханно разбогател. С другой стороны, его представляли как беззаботного мечтателя: по свидетельству одной фракийской служанки, однажды он очень увлекся, наблюдая за небом, и упал в колодец, не заметив того, что находится у него под ногами. (Первую историю поведал Аристотель, а вторую – Платон.) Фалес, как считают некоторые, предсказал солнечное затмение, случившееся во время битвы между лидийцами и персами, которое произошло, как полагают сегодня, 28 мая 585 г. до н. э. Достоверность этой истории долго подвергалась сомнению, и, скорее всего, она на самом деле не соответствует действительности и может рассматриваться лишь как пример мифотворчества, существовавшего во времена Аристотеля.
Именно Аристотель поставил перед своими учениками задачу написать краткую историю человеческого знания. Евдему Родосскому были поручены астрономия и математика, и от него нам известно про поездку Фалеса в Египет, откуда тот привез свои познания в Грецию. Другие утверждали, что Фалес заимствовал их у вавилонян. Даже если и так, у нас не сохранилось никаких свидетельств о таком заимствовании. Утверждалось также, будто именно он, а никто другой, познакомил своих соотечественников с методами геометрического доказательства; но доводы в пользу этого крайне малоубедительны и не принимают в расчет более вероятного соображения, что европейская традиция полуформального геометрического доказательства имеет гораздо более древнее происхождение.
Анаксимандр и Анаксимен придерживались космологических взглядов, столь же схожих, как их имена. Второй философ, вполне вероятно, был учеником первого, они жили в период упадка Сарды (546 в. до н. э.). Как и Фалес, оба родились в Милете, самом южном из всех крупных ионийских городов Малой Азии (как и Сарды, расположенные на западной окраине современной Турции) – факт, напоминающий нам о том, насколько широко простиралась цивилизация, которую мы сегодня называем Древней Грецией. Если вспомнить других великих древнегреческих астрономов и математиков, то Евдокс был из Книда, Аполлоний – из Перги, Аристарх – из Самоса, а Гиппарх – из Никеи и Родоса; все эти города находились либо непосредственно на побережье Малой Азии, либо недалеко от него. И Евклид, и Птолемей обучались в Александрии, хотя и с интервалом в более чем четыре столетия; Архимед жил и творил в Сиракузах, на Сицилии.
Об Анаксимандре говорят, что он изготовил карту обитаемого мира и создал космологию, объясняющую физические свойства Земли и ее обитателей. Согласно его учению, бесконечная Вселенная порождает из себя бесконечное множество миров, и наш мир является только одним из них; он отделяет себя от всего и поддерживает единство своих частей посредством их вращательного движения. (Аналогия с вихревым движением, вероятно, в большей степени относилась к наблюдениям за работой варочных котлов, а не связочных канатов. Подобного рода теории отстаивались еще во времена Ньютона.) Воздушные и огненные массы, как предполагалось, выносятся за пределы мира и образуют звезды. Земля представляет собой круглый парящий диск, а Солнце и Луна – кольцевидные тела, окруженные воздухом. Под воздействием Солнца в воде образовались живые существа, а мужчины и женщины произошли от рыб.
Какими бы дикими ни казались сегодня эти воззрения, в них можно различить далеко не тривиальный способ построения научного рассуждения. Когда Анаксимен, развивая идеи Анаксимандра, утверждает, что воздух является бесконечной первичной субстанцией, из которой путем сжатия и разряжения произошли все остальные тела, он строит логические суждения, основанные на повседневном опыте. (Впрочем, их выбор не всегда был удачен. Он рассматривает дыхание через сжатые и раскрытые губы, вдыхание холодного воздуха и т. п.) Как и Анаксимандр, он вводит вращательное движение, являющееся ключом к пониманию того, каким образом небесные тела могли образоваться из воздуха и воды. Такого рода попытки физического объяснения сотворения мира характерны для большинства древнегреческих мыслителей, и тот факт, что в те далекие времена они весьма слабо сочетались с вращением небесных тел, а также с тем, как они движутся после того, как уйдут под горизонт – за край видимого мира, – нисколько не умаляет их ценности для последующей истории космологического знания. Вопросы всегда предшествуют ответам.
Такой великий человек, как Пифагор, не нуждается в представлении, хотя знаменитая геометрическая теорема, благодаря которой его помнят, на деле не имеет к нему почти никакого отношения, по крайней мере в ее евклидовой формулировке и по сей день преподаваемой в школах. Он жил на рубеже VI–V вв. до н. э. Несмотря на мощь оказанного им религиозного влияния, до нас не дошло ни одного его сочинения, за исключением нескольких разрозненных свидетельств. Однако, скорее всего, он продвинулся на шаг вперед в развитии космических представлений Анаксимандра и Анаксимена, предположив, что Вселенная была сотворена Небесным Вдохом (обратите внимание на метафору) – Бесконечностью – таким образом, чтобы в ней появились совокупности чисел. Почему чисел? Ему приписывается утверждение, согласно которому все вещи являются числами. Он особенно гордился открытием арифметических законов построения музыкальных интервалов. Это открытие дало начало мистическим течениям нумерологии, по сей день имеющей своих приверженцев. Похоже, Пифагор был убежден в том, что буквально все – от мнений, возможностей и предубеждений до далеких звезд – берет свое начало в арифметике и занимает соответствующее место в структуре Вселенной, понимаемой как единое целое. Вне зависимости от того, насколько обоснованы были такие верования, начиная с этого момента сложно найти период в истории, когда такие убеждения не оказывали бы серьезного влияния на научную мысль.
Благодаря Аристотелю мы знаем, что космологическая система, предложенная пифагорейцами, состояла из центрального огня, вокруг которого обращались по круговым орбитам все небесные тела, включая Землю. Эту систему обычно приписывают пифагорейцу Филолаю из Кротона. Ее часто путают с системой Коперника, однако центральный огонь не являлся Солнцем, которое, как считалось, тоже обращалось вокруг огня, двигаясь выше орбиты Земли. В пределах земной орбиты, как предполагалось, находится еще один объект, так называемая «противоземля», введенный для учета лунных затмений. В целом эта система являлась скорее порождением разума, чем результатом наблюдений. Однако она была составлена в характерном греческом стиле, с привлечением рациональной и физической компонент, что в конечном счете принесло свои плоды, когда удалось включить в нее достоверные наблюдательные данные.
ГРЕЧЕСКИЕ КАЛЕНДАРНЫЕ ЦИКЛЫ
Похоже, зодиак, зародившийся в Месопотамии в начале первого тысячелетия до н. э., не был известен грекам вплоть до V в. до н. э. Его греческая версия, как мы знаем, стала использоваться только во второй половине указанного столетия, поскольку именно тогда ее начали употреблять в парапегмах – звездных календарях, где зодиакальные знаки применялись для деления года. (Точное значение слова «парапегма» – доска для публичных объявлений, однако известно, что слово способно нести в себе почти любую вложенную в него информацию.) Метон и Евктемон, расцвет их деятельности приходится на 430 г. до н. э., были афинскими астрономами, имена которых часто упоминались в парапегмах. Поскольку до греко-персидских войн V в. до н. э. и греки, и вавилоняне находились в подчинении у персов, нет ничего удивительного в использовании греками вавилонского зодиака, дополненного знаками Овна и Весов. Вероятно, влияние вавилонян распространялось и на другие сферы. Солнцестояния наблюдались с незапамятных времен, но теперь регистрация сезонных событий стала вестись с особой тщательностью. Это делалось в целях усовершенствования гражданского календаря или для улучшения календарной системы, в которую подставлялись данные астрономических наблюдений. Примерно за сто лет до наступления золотого века Евдокса, Платона и Аристотеля греки стали проявлять озабоченность в отношении усовершенствования гражданского календаря, однако эта задача не воспринималась ими как строго астрономическая, что с очевидностью следует из того, насколько редко и с каким опозданием магистраты вносили исправления в случае, если сбивались солнечный и лунный циклы. Это могло быть также следствием простого непонимания магистратами сути стоящей перед ними проблемы.
Вне зависимости от того, являлись Метон и Евктемон основателями новой астрономической «школы» или нет, они, по всей видимости, сотрудничали друг с другом, пытаясь создать усредненный 19-летний годовой цикл – так называемый Метонов цикл. По преданию, Метон установил инструменты для наблюдения солнцестояний на холме Пникс в Афинах, и, по свидетельству Птолемея, сделанному шестью столетиями позже, эти два астронома провели наблюдения в Афинах, на Кикладах, в Македонии и Фракии. Вавилонянам, как мы уже видели, были знакомы свойства 19-летнего периода, по истечении которого солнечный и лунный циклы снова приходили в соответствие друг с другом. Действительно, продолжительность 235 месяцев дает очень хорошее совпадение с 19 годами. Сегодня считается общепризнанным, что 19-летний цикл был известен в Месопотамии еще до V в. до н. э. Метон и Евктемон произвели наблюдение летнего солнцестояния (хотя спустя много лет надежность этого наблюдения была поставлена под сомнение Гиппархом и Птолемеем) 27 июня 432 г. до н. э. И вавилоняне, и греки выработали на основе этого цикла сходные друг с другом правила интеркаляции, заключавшиеся во введении дополнительных дней (как у нас лишний день в високосном году) для коррекции календарных сдвигов: согласно Птолемею, Метон считал 235 месяцев равными 6940 дням. В I в. до н. э. Гемин, живший на Родосе, в своем сочинении «Введение в астрономию»1 отчетливо разъяснил: целью эллинов было разделить солнечный год на месяцы таким образом, чтобы традиционные праздники приходились на одни и те же дни одних и тех же месяцев. Он проверил несколько традиционных моделей такого деления и указал на их ошибки. В той же книге он аналогичным образом интерполировал значение, полученное вавилонянами для продолжительности синодического месяца. (Эта интерполяция сделана с некоторым запозданием, однако Птолемей, живший двумя столетиями позже Гемина, был первым известным нам грекоговорящим астрономом, имевшим в своем распоряжении результаты вавилонских расчетов. Благодаря Птолемею они перешли в арабскую, римскую и иудейскую традиции.) В тексте Гемина продолжительность синодического месяца оценивается как 29 + 1/2 + 1/33 суток. В его версии календаря, состоящего из 235 месяцев, 110 месяцев были «пустыми» и содержали по 29 дней, а 125 – «полными» и содержали по 30 дней. Задолго до этого Метон, возможно, разработал собственный алгоритм интеркаляции, однако даже если это и так, нет никаких надежных свидетельств его использования в афинском гражданском календаре. Впрочем, история календаря настолько запутана и противоречива, что в этом вопросе имеет смысл сохранять непредвзятость в отношении любого мнения.
Вне зависимости от того, открыли вавилоняне 19-летний цикл до или после афинян, они использовали другие правила интеркаляции, основанные на восходе Сириуса, упоминание о которых относится примерно к тому же времени, что и упоминание о 19-летнем цикле, и, скорее всего, как представляется, они опередили греков по всем статьям. Тем не менее календарные циклы образовали у греков своего рода особую астрономическую специализацию. Через сто лет после Метона и Евктемона, Каллипп усовершенствовал их цикл, взяв четыре периода (76 лет) и удалив один день (это давало в совокупности 27 759 дней). Калиппов цикл использовался впоследствии в модифицированной форме Гиппархом и Птолемеем. Тонкая доработка, произведенная Гиппархом (приравнивание 304 лет к 111 035 дням и 3760 синодическим месяцам), по всей видимости, не нашла широкого практического применения. Более простые циклы по 19 и 76 лет были вполне достаточны для большинства обыденных нужд, а 19-летний цикл в итоге лег в основу методики расчета пасхалий (computus) восточной христианской церкви, где используется и по сей день.
ДРЕВНИЕ ГРЕКИ И НЕБЕСНАЯ СФЕРА
Греческая астрономия V в. до н. э., как и астрономия Ближнего Востока, была неразрывно связана с общим изучением метеорологических явлений – облаков, ветров, гроз и молний, падающих звезд, радуг и т. д. Эта компонента (наряду с астрологическим подтекстом) была присуща ей вплоть до Нового времени, однако в долгой перспективе гораздо более важными оказались зачатки геометрического метода, содержащиеся в операциях, производимых древними греками. Традиция приписывает открытие сферичности Земли Пармениду из Элеи (Южная Италия), родившемуся около 515 г. до н. э. Он, как считается, также открыл то, что Луна светит отраженным солнечным светом. Спустя поколение Эмпедокл и Анаксагор сумели, похоже, дать правильное математическое разъяснение причин, вызывающих солнечные затмения, а именно – покрытие солнечного диска Луной, вошедшей в пространство между Землей и Солнцем. Рост астрономического знания в течение периода, приведшего в IV в. до н. э. к началу первой эпохи грандиозных математических открытий, осуществлялся эпизодически и почти незаметно. IV в. начался со знаменитой планетной теории Евдокса и закончился первым дошедшим до нас трактатом по сферической астрономии, написанным Автоликом и Евклидом. Этому предшествовали небольшие, но очень важные усовершенствования. По преданию, в V в. до н. э. Демокрит составил звездный каталог, и многие последовали его примеру, хотя об этом можно судить только по косвенным данным. Вероятно, в большинстве случаев это были всего лишь иллюстрированные списки звезд. Вплоть до Гиппарха не существовало ничего, что могло бы однозначно свидетельствовать о единообразной греческой системе сферических координат, посредством которых звездные каталоги могли приобрести реальную астрономическую ценность.
Важным шагом на этом пути был переход от перечисления звезд с привязкой к зодиакальным созвездиям к системе численных эклиптических долгот, совершенный вавилонянами около V в. до н. э. На протяжении следующих шести столетий ни у кого не возникало мысли вести отсчет (как мы делаем это сегодня) от нулевой точки, расположенной на пересечении экватора и эклиптики. Птолемей ввел в употребление этот способ для введения определения (тропического) года. Вавилоняне вели отсчет от нулевых точек каждого зодиакального знака, внутри которых значения менялись от 0° до 30°. Эта система долгое время использовалась (и, можно даже сказать, используется по сей день) в астрологии. Вавилонские знаки сместились на 8° или 10° (в системах B и A соответственно) относительно тех мест, где их располагали последователи Птолемея, и мы уже упоминали о следах этого расхождения, обнаруженных в западноевропейских средневековых источниках, где эта идея механически повторялась учеными, имевшими весьма туманное представление о том, к чему она относилась на самом деле. Несмотря на кажущуюся примитивность этой системы, в V в. до н. э. у греков не было ничего, что могло бы ей противостоять.
ГОМОЦЕНТРИЧЕСКАЯ СИСТЕМА ЕВДОКСА
Открытие сферичности Земли и преимуществ описания неба, понимаемого в виде сферы, захватило воображение греков эпохи Платона и Аристотеля и в особенности человека по имени Евдокс Книдский (ок. 400–347 гг. до н. э.), разработавшего весьма незаурядную планетную теорию, целиком основанную на сферических движениях. По части предсказательной способности эта теория не выдерживала сравнения с вавилонскими арифметическими схемами, однако она была очень важна во многих других отношениях. Во-первых, она продемонстрировала последующим поколениям огромную мощь геометрических методов; и во-вторых, благодаря случайному стечению обстоятельств – признанию ее Аристотелем – она на два тысячелетия стала инструментом создания философских представлений о главных принципах устройства мироздания.
Евдокс был родом из Книда, города в древней Спарте, расположенного на полуострове в юго-западной части Малой Азии. В молодые годы он изучал музыку, арифметику и медицину, а также обучался геометрии у знаменитого математика Архита Тарентского. В свой первый приезд в Афины он учился у Платона, который был старше его на тридцать лет. Позже он посетил Египет, вероятно, с дипломатической миссией, и, как говорят, составил восьмилетний календарный цикл (octaёteris) во время обучения у жрецов из Гелиополя. Возвратившись в Малую Азию, он основал школу в Кизике, ставшую конкурентом академии Платона в Афинах – городе, где он побывал по меньшей мере еще один раз. (Кизик – греческий город, сданный персам в 387 г. до н. э.) Он исповедовал теорию, согласно которой удовольствие является высшим благом, и, похоже, именно его имел в виду Платон, когда писал об этом в своем сочинении «Филеб». Было ли это так на самом деле – неизвестно, но Евдокс существенным образом повлиял на развитие арифметики, геометрии и астрономии. Именно ему принадлежит главная заслуга в написании самых знаменитых разделов «Начал геометрии» Евклида (Книги V, VI и XII) – одного из наиболее авторитетных сочинений в истории образования. Заслуги Евдокса в строгом определении понятия числа, которое, как выяснилось позже, имеет много общего с определениями Дедекинда и Вейерштрасса, сформулированными в XIX в., до сих пор не оценены по достоинству. Однако его планетная теория привлекла к себе внимание с момента появления и продолжала вызывать спорадический научный интерес вплоть до XVI в.
В предпоследнем разделе предыдущей главы мы обсуждали особенности движения планет с точки зрения упрощенных современных представлений. Часто утверждалось (со ссылкой на авторитет гораздо более позднего автора Симпликия, а он, в свою очередь, цитировал Созигена), что именно Платон был тем человеком, который поставил перед своими потомками проблему объяснения того, как наблюдаемые движения планет могут быть объяснены через «единообразное и упорядоченное» движение небес. (Гемин мимоходом упоминает: пифагорейцы первыми поставили этот вопрос, исходя из нелепости предположения, будто планеты могут двигаться как-то иначе.) Несмотря на постоянный интерес, вызываемый воззрениями такого выдающегося философа, как Платон, его достижения в области математики и астрономии слегка преувеличены. Его вклад в эти науки был, скорее, косвенным; он обусловлен его убеждением, будто обе науки должны стать частью образования правящего класса – как представителей власти, так и рядовых граждан. Его влияние как пропагандиста еще достаточно сильно, чтобы считаться с ним: он рассматривал эти занятия как средство воспитания души, позволяющее увидеть за преходящими вещами бренного мира истинную реальность, доступную постижению лишь с помощью мысли. Астрономические суждения Платона были случайны и беспорядочны, однако в целом его достижения невозможно переоценить. Красноречиво настаивая на том, что Вселенная приводится в движение сообразно с математическими законами, которые могут быть постигнуты только подготовленным соответствующим образом разумом, он способствовал возникновению общего педагогического климата, благоприятного для этой науки.
Открытие сферической формы Земли и перенос идеи сферичности на небеса всецело овладели умами афинских мыслителей времен Платона. В десятой книге одного из лучших своих сочинений «Государство» Платон приводит миф, образно и поэтично рассказанный ему его учителем Сократом. Это история об убитом в бою человеке по имени Эр, чья душа посетила царство мертвых, но вернулась в тело после чудесного воскрешения Эра. Сократ рассказывает, как его душа направляется сначала в некое волшебное место, описанное им довольно подробно, и как, после всего увиденного, ему удалось рассмотреть устройство механизма всей планетной системы – со свивающимися одно над другим кольцеобразными завихрениями, которые в одном из возможных вариантов перевода называются «чашами», а в другом – «обручами». Они вращаются вокруг стального веретена, и каждая (каждый) несет на себе планету. Веретено покоится на коленях у Необходимости; ей доверено осуществлять суточное обращение неба и движение планет. Завихрения приводятся во вращение с разными характеристическими скоростями богинями Судьбы (дочерьми Необходимости), и на каждом из них находится Сирена, издающая звук определенной высоты – такой, чтобы все вместе они образовывали гармоничное звучание.
В этом описании нигде не встречается Противоземля пифагорейцев. Нет и намека на расположение зодиака под углом к экватору; впрочем, было бы наивно погружаться во все подробности мифа об Эре в целях поиска таких тонкостей. Единственное, о чем этот миф свидетельствует с достаточной достоверностью, – это о том, что в те времена действительно разрабатывались физические модели Вселенной и они имели не только умозрительный характер. Для описания вселенной Эра без опоры на реальную модель необходимо вести рассуждение о замкнутых сферических оболочках; однако в этом случае реальная модель должна была содержать съемную крышку, заглянув под которую люди могли бы увидеть то, как она работает. В своем позднем сочинении «Тимей» Платон описывает то, как Демиург создает вселенную из четырех основных элементов, и использованные им слова воспринимаются более ясно, чем подразумеваемая им реальная картина мира. Предметом его описания являются уже не концентрические завихрения, а обычная армиллярная сфера – астрономическая модель небесной сферы, изготовленная из колец, которые не заслоняют собой ее внутреннего устройства.
В другом сочинении Платона – «Законы» – некий Афинский Странник говорит, что он был уже далеко не молодым человеком, когда уразумел: каждая планета движется по своему собственному пути, и поэтому ошибочно называть их «блуждающими». В «Государстве» Платон называл их хаотичными. Это утверждение, вполне вероятно, автобиографично, и заманчиво предположить, что именно Евдокс был тем человеком, который заставил Платона поменять свое мнение. Планеты называли «блуждающими» из‐за возникающего время от времени попятного движения, но их подчиненность геометрическому порядку (если только он обнаруживался) демонстрирует не такую уж и хаотичность их перемещений.
Оригинальные сочинения Евдокса не сохранились, но его систему можно восстановить по сочинениям двух других мыслителей, в особенности его младшего современника Аристотеля, а также Симпликия. Симпликий был платоником, написавшим ценные комментарии к работе Аристотеля, однако его нельзя считать математиком. Поскольку он родился около 500 г., а умер позже 533 г. н. э., его свидетельства, записанные спустя 900 лет после описываемых событий, могли быть расценены как малодостоверные, если бы не пара-тройка крайне важных замечаний. Из теоретических построений Евдокса следует, пишет он, что форма планетной траектории представляет собой гиппопеду (это означало путы для лошади, сделанные в виде восьмерки); он упоминает также о недружелюбной критике в адрес Евдокса, поскольку тот приписал траекториям такую характеристику, как ширина. Если рассмотреть в совокупности общие положения этой теории, с которыми и сам он, и Аристотель были более или менее согласны, то, как мы покажем далее, можно узнать о ней очень многое.
Система Евдокса построена из концентрических сфер, центры которых совпадают с Землей. Они вложены друг в друга, но это вселенная математика, где не принимаются в расчет их относительные размеры. Идея обязательного привлечения сфер кажется сегодня очевидной, но введение таких сфер – реальных или воображаемых – неизменно становилось предметом дальнейшего обсуждения. Например, нетрудно понять, что для описания Солнца требуется как минимум две сферы, одна – для быстрого суточного вращения, а другая – для годового движения Солнца в противоположном направлении. Вторая сфера, очевидно, должна вращаться вокруг полюсов эклиптики. Аналогичным образом может быть описана Луна. (И в том и в другом случае предполагается, что объект находится примерно посередине между полюсами сферы, к которой он относится.) На деле, Евдокс вводит дополнительную третью сферу как для Солнца, так и для Луны. В случае Луны, вполне возможно, она предназначалась для учета наклона лунной орбиты к эклиптике под углом примерно пять градусов; она пересекает ее в определенных точках (узлах), медленно движущихся по зодиаку в обратном направлении. (Как показано в предыдущей главе, узлы описывают полный круг по небу примерно за 18,6 года.) Источником этой догадки могли стать рудиментарные представления о затмениях. Если именно это стало причиной введения третьей сферы, то и Аристотель, и Симпликий ошиблись в порядке расположения второй и третьей лунных сфер, но, в принципе, их расчеты не были лишены смысла. Вызывает определенное недоумение введение Евдоксом дополнительной третьей сферы еще и для движения Солнца, судя по всему, основываясь на том, что в дни зимнего и летнего солнцестояний Солнце не всегда восходит в одной и той же точке горизонта. Симпликий утверждает, будто те, кто жил до Евдокса, размышляли об этом. Эта идея повторялась и несколькими более поздними авторами.
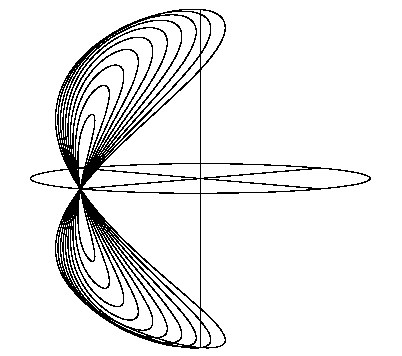
41
Серия гиппопед. Для каждой из планетных моделей Евдокса требовалась только одна гиппопеда, но мы можем убедиться в том, как, выбирая из этого ассортимента, он имел возможность дать объяснение широкому спектру движений как по широте, так и по долготе.
Именно его интерпретация прямого и попятного движения планет придала вращающимся сферам Евдокса вид канонической модели. Далее он демонстрирует, каким образом точка может описывать фигуру в виде восьмерки, которая, в свою очередь, переносится по небу более длительным планетным движением, находясь более или менее в пределах зодиака. Чтобы получить эту фигуру (гиппопеду), он просто берет пару сфер, одна из которых вращается в одном направлении, а другая – в противоположном направлении с той же скоростью вокруг оси первой сферы, не совпадающей с осью ее собственной (второй) сферы. Для наглядности на ил. 41 изображены десять обсуждаемых здесь математических кривых, соответствующих различным углам наклона двух упомянутых осей. Теперь нужно рассмотреть движение планеты вдоль этой ∞-образной траектории, развернув его во времени. Нетрудно представить, каким образом перенос ее вдоль зодиака (или в близкой от него области) будет время от времени давать попятное движение при обращении вокруг оси, расположенной под прямым углом к длине гиппопеды. К этому третьему движению необходимо добавить суточное вращение неба, так называемое «вращение неподвижных звезд».

42
Общий характер планетной траектории по Евдоксу; качественно допустимый, но неосуществимый в реальности
Если не принимать во внимание это третье вращение, то общий вид траектории движения будет таким, как показано на ил. 42; рисунок точно воспроизводит форму кривой, но параметры скорости и наклона осей выбраны на нем произвольно. Мы отложим на время вопрос о точном воспроизведении планетных движений, как они наблюдаются на самом деле.
Применяя такую аппроксимацию к движению планет, по крайней мере качественно, можно свести кажущееся хаотичное перемещение к закономерному. Это открытие, без сомнения, вызвало восторг у Платона. Однако какую цель ставил перед собой сам Евдокс? Есть все основания полагать, что восхищение, которое вызвало у греков предложенное им объяснение, относилось не столько к предсказательной силе теории, сколько к ее геометрическим достоинствам. Для оценки реального характера достижений Евдокса необходимо хотя бы в общих чертах воспроизвести ее геометрическую реконструкцию, предложенную в 1870‐х гг. талантливым итальянским астрономом Джованни Вирджинио Скиапарелли. Используя известные теоремы греческой геометрии, уже употреблявшиеся во времена Евдокса, он показал, что гиппопеда является линией пересечения цилиндра со сферой, на которой лежит эта кривая. Цилиндр при этом, как предполагается, изнутри касается сферы (см. ил. 43).
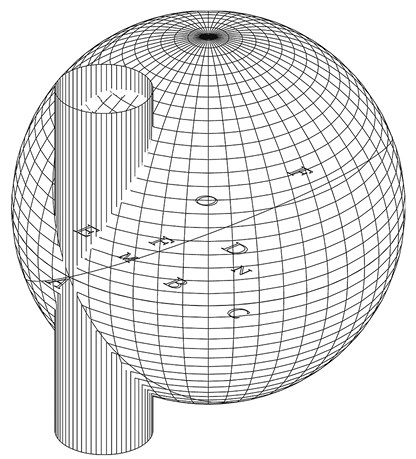
43
Гиппопеда как кривая, получающаяся при пересечении сферы и цилиндра, касающегося ее изнутри. Буквенные обозначения соответствуют приведенным на ил. 44.
Этот красивый геометрический вывод, лишь отдаленно напоминающий описания, составленные Аристотелем и Симпликием, был не так уж и чужд рассматриваемой эпохе. Учитель Евдокса Архит, решая проблему удвоения куба, рассматривал пересечение трех поверхностей вращения – тора (якорного кольца), конуса и цилиндра. Те, кто считает, будто Евдокс не мог оказаться вне этого тренда, но не выражает желания рассуждать об этом в категориях трансцендентных кривых четвертого порядка, могли бы дополнить сферу и цилиндр еще одной простой поверхностью, где можно расположить гиппопеду. Это некая поверхность, постоянным сечением которой является парабола. (Представьте лист бумаги, согнутый таким образом, чтобы два его противоположных края образовывали две одинаковые параболы, тогда линия гиппопеды будет полностью лежать на этом листе.) У нас нет убедительных доказательств того, знал ли Евдокс об этом свойстве изобретенной им гиппопеды, однако то же самое может быть со всей строгостью применено и к сечению цилиндра. Исходно сам Евдокс, скорее всего, рассуждал именно в этих категориях, хотя, когда средневековые и ренессансные астрономы узнали о подобных моделях, они выказали их непонимание, во всяком случае в некоторых аспектах.


