
Джон Норт
Космос. Иллюстрированная история астрономии и космологии
44
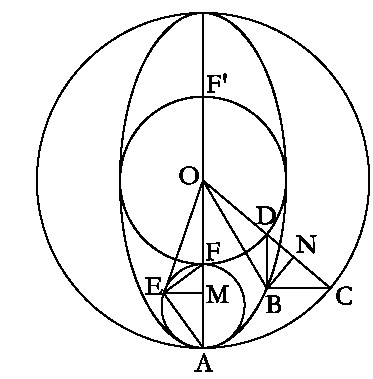
Вспомогательная схема, позволяющая понять геометрию гиппопеды. Диаграмма вписана в центральную плоскость ил. 43.
Модель Евдокса оказалась столь значима в истории геометрической астрономии, что нам просто необходимо доказать ее хотя бы схематично для демонстрации элегантности астрономической доктрины, разработанной более двадцати трех столетий назад. Будем различать несущую и несомую сферы. На ил. 44 направление взгляда (сверху) совпадает с осью первой сферы и параллельно оси цилиндра, на поверхности которого находятся точки F, E и A. (Поучительно будет спросить, почему этот цилиндр не параллелен другой оси; или, например, не расположен симметрично между ними.) A – исходная точка планеты, а дуга AB – ее движение вдоль экватора несомой сферы за какое-то время. Если смотреть сверху, то он (экватор) будет казаться эллипсом, а угол AOB, как он виден на рисунке, – будет меньше реального трехмерного угла. На самом деле он равен изображенному на рисунке углу AOC, где C – это точка, отделившаяся от A в тот же момент времени, что и точка В, но движущаяся по другому кругу. Точки B и C, очевидно, будут располагаться на одном и том же уровне (CB образует перпендикуляр с OA). Рассмотрим теперь, как это составное движение планеты будет осуществляться во времени, если наблюдать за ним в плоскости диаграммы (то есть ортогональной проекции на эту плоскость). Планета движется вверх до точки B несомым движением и дополнительно поворачивается движением несущей сферы, осуществляющей перенос отрезка OB в OE; причем угол BOE равен углу AOC. Необходимо доказать, что точка E лежит на линии сечения цилиндра. Если угол CBD прямой, а точка D лежит на отрезке OC, то достаточно показать неизменность длины отрезка CD; поскольку в этом случае вся совокупность точек типа D (включая F) будет лежать на окружности с центром в O. Угол FEA также будет прямым, поэтому точка E будет лежать на окружности с диаметром FA, то есть на сечении цилиндра.

45
Точное изображение модели Евдокса в применении к Юпитеру. Представлен вид трехмерной траектории в перспективе.
Проще всего получить доказательство постоянства длины отрезка CD, используя свойства эллипса, но, рассматривая соответствующую часть диаграммы в трех измерениях, несложно провести доказательство, основанное на отношении сторон подобных треугольников. Это легче, чем осуществить первичную визуализацию; и уж точно легче, чем доказать теорему о параболическом листе. Я бы хотел только добавить, что фокус этой параболы является четвертой частью расстояния от A до F.
Здесь мы имеем дело с задатками впечатляющей геометрической модели планетного движения, но, как это ни прискорбно, она, если брать ее в чистом виде, обладает рядом существенных недостатков. Иногда истина искажается. Неверно будет полагать, будто все витки попятного движения планет идентичны друг другу (как показано на ил. 42); неверно и то, что смещение планеты по широте обязательно должно быть значительным. Попятные движения Сатурна и Юпитера могут быть довольно правдоподобно представлены без поправок для широты (см. ил. 45 для Юпитера). К сожалению, если не вводить добавочных сфер, в этой модели можно свободно менять только два основных параметра: относительные скорости по гиппопеде и самой гиппопеды; и размеры гиппопеды, зависящие от наклона вращающейся сферы. Этих параметров явно недостаточно для согласования модели с действительными движениями Марса, Венеры или Меркурия. Если правильно задать скорости, то длина дуги попятного движения даст чудовищную ошибку, и наоборот.
С современной точки зрения относительные скорости по гиппопеде и самой гиппопеды зависят как от самих планет, так и от угловой скорости Земли при ее обращении вокруг Солнца, а размер гиппопеды по отношению к сфере зависит от относительных размеров планетных орбит при их вращении вокруг Солнца, включая нашу планету. Не углубляясь в детали, заметим следующее: в первом случае факты, очевидно, могут потребовать движение самой гиппопеды с такой высокой скоростью по сравнению со скоростью находящейся на ней планеты, что фаза попятного движения окажется просто нереализуемой. Именно это и происходит в упомянутых примерах. И во втором случае, если мы зафиксируем в нашей модели длину дуги попятного движения в строгом соответствии с наблюдениями, это вынудит нас принять как следствие получившуюся гиппопеду, независимо от того, какой будет ее ширина. Дело не только в ее чрезмерной величине для Марса и Венеры, но еще и в том, что в этом случае планетное движение по широте имеет весьма отдаленное отношение к орбитальным размерам. Это обусловлено преимущественно расположением планетных орбит, включая орбиту Земли, в близких друг к другу, но разных плоскостях.
КОСМОЛОГИЯ АРИСТОТЕЛЯ
По поводу моделей Евдокса существует много вопросов, оставшихся без ответа, или вовсе не имеющих ответа, и они касаются не только мотивов, понудивших его создать свою систему. Поскольку местом, где он учительствовал, была малоазийская греческая колония (Кизик находится на южном побережье Мраморного моря, к юго-востоку [через море] от современного Стамбула), не исключено, что ему были знакомы астрологические и религиозные аспекты астрономического знания. Однако к тому времени интеллектуальные предпочтения греков уже не совпадали с предпочтениями их азиатских соседей. Вероятно, греки не воспринимали поклонение звездам как нечто абсолютно враждебное, но в их религии этим вопросам отводилась второстепенная роль, как, собственно, и вопросам поклонения Солнцу и Луне, хотя у них и были соответствующие божества, персонифицированные в Гелиосе и Селене. Когда великий поэт и драматург Аристофан, умерший примерно тогда же, когда родился Евдокс, характеризовал различие между религией греков и иноземцев, он отмечал, что если последние обожествляли Солнце и Луну, то греки совершали подношения персонифицированным богам – таким, как Гермес. Эллинистическая религиозная традиция долгое время находилась в стороне от бесхитростных древних небесных религий, хотя спустя несколько столетий после возникновения восточной астрологии этот тренд поменялся.
Во времена Евдокса философы, не смущаясь, включали небесные тела в свои пантеоны. К ним, считал Пифагор, нужно относиться как к божествам, а Платон признавался, что был потрясен атеистическим утверждением Анаксагора, будто Солнце – это горящая масса, а Луна подобна Земле. Платон полагал: звезды – это видимые изображения богов, порожденные всевышним и вечным Богом. Бога больше не существовало как небесной религии простолюдинов, но Он стал религией интеллектуалов-идеалистов, и благодаря усилиям многочисленных последователей, многие из которых были христианами, представления Платона о небесах оказались весьма влиятельными. Даже его оппонент Аристотель отстаивал идею о божественном происхождении звезд, представляя их как вечное вещество, находящееся в неизменном движении. Конечно, это божества, но все это совершенно не похоже на халдейские доктрины, претендующие на предсказание по небесным знакам жизни и смерти народов и отдельных людей, а также погоды и всего с ней связанного.
Мы не можем сказать с определенностью, каковы суждения Евдокса по этим вопросам, но вряд ли можно сомневаться в том, что в своей астрономической теории он был движим главным образом интеллектуальным удовольствием геометра – тем ресурсом, весомость которого часто недооценивается многими социальными историками. Хотя письменное свидетельство римского государственного деятеля и ученого Цицерона в сочинении «О природе богов» является относительно поздним (он умер в 42 г. до н. э.), именно Евдокс, по его мнению, утверждал: «Не следует верить халдеям, которые предсказывают и размечают жизнь каждого человека по дню его рождения». Во времена Цицерона римский мир вполне трезво относился к практикам такого рода, и исходя из этого многие считали эту ссылку анахроничной, однако нет никаких причин, из которых следует, что это было именно так. В действительности, она могла быть взята из источника, содержащего отсылку к способам неастрономического предсказания человеческой жизни, поскольку у вавилонян существовали технические приемы, позволяющие делать это, и они были известны в Египте задолго до Евдокса, опиравшегося только на календарь. Однако если дело обстояло именно таким образом, то это лишает силы аргумент, согласно которому Евдокс сознательно отвергал астрологию в ее наиболее известных формах.
Каковы бы ни были его мотивы, мы не можем уверенно судить об успешности всех его достижений, когда сравниваем их с более поздними астрономическими изысканиями и с устремлениями вавилонян. Тот факт, что мы способны подогнать движения Юпитера и Сатурна к предложенной им модели, не означает, будто сам Евдокс делал это с такой же точностью. У нас легко получается менять параметры этих конструкций, например изменяя скорости несущей и несомой сфер, но другие – те, кто жил в античные времена, – не обязательно делали то же самое. Эти действия приводят по большей части к не таким уж приятным последствиям. Среди наиболее любопытных геометрических следствий можно отметить следующее: в базовой системе, состоящей из двух сфер, удвоение угловой скорости несущей сферы по отношению к скорости несомой сферы даст в итоге кривую, которая будет являться обычной окружностью, наклоненной в сторону, противоположную наклону экватора несомой сферы. Возможность появления таких вариантов должна внушить нам осторожность в отношении спекуляций на тему истинных причин следующего шага в развитии общей теории, сделанного Каллиппом из Кизика около 330 г. до н. э.
Каллипп был учеником Полемарха, а тот, в свою очередь, учился у Евдокса; он последовал за Полемархом в Афины, где остановился у Аристотеля, для «исправления и дополнения с помощью Аристотеля открытия Евдокса». Так свидетельствует Симпликий, сообщающий нам, что Каллипп увеличил количество сфер, добавив по две для Солнца и Луны и по одной на каждую планету, кроме Юпитера и Сатурна. Именно эти планеты – та самая пара планет, которая, как мы сами могли убедиться, подходит нам наилучшим образом – в достаточной мере удовлетворяли модели Евдокса. При данных обстоятельствах, сколь ни печально это признавать, мы вынуждены согласиться с тем, что в этот период греки занимались построением только качественной модели попятного движения. Симпликий идет дальше и утверждает, будто Евдем составил список явлений, которые понудили Каллиппа усложнить систему.
Понимали ли греки преимущества новой модели по сравнению со старой? Общее число сфер у Евдокса равнялось 26, а у Каллиппа – 33, однако перечисленные здесь суммарные числа не должны вводить нас в заблуждение, заставляя думать, что каждый из них намеревался построить единую систему – одну для всех планет. Насколько можно судить, они оба довольствовались обоснованием моделей, построенных отдельно для каждой из планет или светил. Однако, каковы бы ни были введенные Каллиппом усовершенствования, Аристотель, как нам известно, подробно рассмотрел его идеи и превратил в унифицированную механическую систему то, что напоминало, скорее всего, набор отвлеченных геометрических теорий. Вот почему эта теория заняла столь важное место в натуральной философии на целых два тысячелетия.
Вне всяких сомнений, Аристотель – наиболее выдающийся античный философ науки. Он родился в Стагире в 384 г. до н. э. в обеспеченной семье: его отец был личным врачом деда Александра Македонского, а сам Александр являлся воспитанником Аристотеля. Аристотель учился в Афинах у Платона до самой смерти последнего в 348 г. до н. э. и, после нескольких переездов сначала в Мизию, потом на Лесбос и в Македонию, возвратился в Афины, где основал собственную философскую школу, так называемый Ликей. Его объемные сочинения весьма систематичны, связаны друг с другом и охватывают широкую область человеческого знания. Поскольку они писались в течение продолжительного периода времени, в них, безусловно, можно обнаружить несколько незначительных противоречий. Наиболее важный, стоящий отдельно ото всех источник по космологии Аристотеля – его «De caelo» (в переводе это означает «О небе», но чаще употребляется в латинском написании) – был ранним трактатом, в который не вошло ничего из его крупнейших нововведений в этой области. Например, в нем ничего не говорится о том, что движет, само будучи недвижи́мым; об этом нам приходится справляться в его «Физике». Этот, как считалось, неподвижный двигатель, или Primum mobile (перводвигатель), располагающийся на крайних пределах Вселенной, был источником движений всех содержащихся в ней небесных сфер.
Аристотель писал в полуисторической манере, составляя обзоры наиболее существенных доводов своих предшественников. Самая большая глава «De caelo» посвящена небесным сферам – теоретической конструкции, к тому времени повсеместно признанной в Греции, а также Земле, тоже обладающей сферической формой и находящейся в центре мира. Он упоминает о теориях пифагорейцев и некой безымянной школы, согласно которым Земля вращается в центре Вселенной. Он отбрасывает эту идею, равно как и орбитальное движение Земли. Сегодня мы безоговорочно принимаем и то и другое. Теория Евдокса, скорее всего, показалась ему убедительной, поскольку в ней подразумевалось, что звезды тоже подвержены «смещениям и поворотам», хотя у нас нет реальной возможности проверить это на опыте. Евдокс, сам того не ожидая, попал в самое «яблочко» своей доктриной о неподвижной Земле. Если бы он был жив, он мог бы указать на относительную убедительность этого аргумента, поскольку звезды находятся на огромном расстоянии от нас.
Аристотель приводит множество аргументов в пользу сферической природы Земли и Вселенной. Естественное движение грубой земной материи, где бы она ни находилась, направлено вниз, к центру, в силу чего вокруг него неизбежно должна образовываться сфера из вещества. Имеется также очевидный наблюдательный факт: линия, разделяющая темную и светлую части лунной поверхности во время лунного затмения, всегда дугообразна – конечно, не самый лучший довод, если рассматривать его отдельно от остальных. Он ссылается на математиков, которые пытались измерить длину окружности Земли – Архита или Евдокса (?) – и получили для этого величину в 400 000 стадий, что соответствует примерно 74 000 километров. Хотя данное значение сильно завышено, это самая ранняя известная нам попытка оценить размеры Земли. (По современным данным, длина земного экватора составляет около 40 075 километров.)
Сфера, говорит Аристотель, представляет собой наиболее совершенную форму твердых тел, так как вдоль какого бы диаметра она ни вращалась, она всегда занимает одно и то же пространство. Он конструирует Вселенную посредством последовательного возведения над сферичной Землей все новых и новых оболочек. Только круговое движение способно совершать бесконечное количество обращений без перемены направления, и вращательное движение превосходит прямолинейное, поскольку то, что вечно, или по меньшей мере могло бы существовать неограниченно долго, то и превосходно или могло бы быть превосходным по отношению к тому, что не вечно. По Аристотелю, круговые движения являются отличительным признаком совершенства. Естественные движения на Земле – это вверх (для дыма и подобных веществ) или вниз (для грубых веществ), в то время как на небесах естественные движения представляют собой круги, не допускающие значительных перемен, которые были бы знáком несовершенства, дефектности. На небесах находятся простые и несмешанные тела, состоящие не из близко знакомых нам по опыту четырех элементов, а именно – земли, воздуха, огня и воды, а из особого пятого элемента – эфира. Степень его чистоты не постоянна и является наименьшей там, где он граничит с воздухом, простирающимся до сферы Луны. (Именно эта идея о существовании пятого, неразложимого элемента, или сущности [essence], дала начало нашему слову «квинтэссенция».)
Тогда-то Аристотель и вводит представление о небесном мире, разительным образом отличающемся от подлунного мира, подверженного переменам и разрушению. Он был единым, не сотворенным и вечным. Эти качества стали источником проблем для христианских последователей Аристотеля. Здесь он выступал против убеждений греческих атомистов Демокрита и Левкиппа, которые отстаивали идеи о существовании пустоты (Аристотель ее отвергал по философским соображениям) и о множественности миров. Он возражал Гераклиту, говорившему о периодической гибели и возрождении Мира, а также Платону, считавшему, что мир сотворен Демиургом.
Это удивительно, но Аристотель оспаривает даже представление о небесной гармонии, подобное обнаруживаемому нами в мифе об Эре. Абсурдно полагать, – говорит он, – будто мы не слышим этого звука, так как он находился в наших ушах с самого рождения. И как в данном случае быть с общим принципом, согласно которому чем больше предмет, тем более громкий звук он издает? Гром во время грозы был бы неразличим на фоне звука, издаваемого громадными небесами. Однако Аристотель не стремится к полному развенчанию идеи небесной гармонии, и его настойчивые утверждения об относительном совершенстве эфирных пространств помогли удержаться на плаву общей платоновской вере в божественную природу небесных тел.
Для уяснения технических деталей планетной системы Аристотеля нам нужно обратиться к его «Метафизике». В ней он, похоже, берет за основу теорию Каллиппа, но если мы примем во внимание его слова «если сложить все эти сферы вместе», то увидим, что на каждое из планетных тел, помимо несущей и несомой сфер (если использовать введенную ранее терминологию), должны приходиться дополнительные «разворачивающие» сферы для компенсации действия внешних сфер, которые не связаны с рассматриваемой планетой. Например, для объяснения движения Юпитера достаточно использовать только его собственные сферы (помимо сферы неподвижных звезд). А если так, то поскольку все сферы Сатурна не имеют отношения к его собственным сферам, они должны быть нейтрализованы добавлением к Юпитеру компенсирующих сфер с такими же полюсами, как и у Сатурна, но с обратными угловыми скоростями. Когда мы перейдем к Марсу, мы должны будем нейтрализовать сферы Юпитера (но не Сатурна, поскольку это уже было сделано ранее); и так для всех планет. У Каллиппа сферы распределялись следующим образом (в скобках указано требуемое количество компенсирующих сфер): для Сатурна – 4 (3), Юпитера – 4 (3), Марса – 5 (4), Венеры – 5 (4), Меркурия – 5 (4), Солнца – 5 (4), Луны – 5 (0). Таким образом, в сумме получается 55 сфер, и Аристотель, действительно, приводит это число. Он оставляет загадочное примечание (так и не поясненное окончательно), что устранение лишних движений Солнца и Луны потребует в общей сложности 47 сфер. На более ранней стадии, как я подозреваю, он вводил 4 компенсирующих сферы для Луны, обеспечивая таким образом неподвижность Земли.
Таким образом, Аристотель ввел механическое представление о Вселенной, состоящей из сферических оболочек. Каждая из них выполняет свою функцию, а некоторые переносят планеты. Движение больше не постулировалось в виде отвлеченных понятий из книг по геометрии и не определялось через категории платоновских идей, но, скорее, формулировалось в терминах физики движения, физики причины и следствия. Первейшая сфера – первое небо – демонстрирует вечное круговое движение, передающееся всем низлежащим сферам; однако что приводит в движение это первое небо? Этот источник его движения сам должен быть недвижимым и вечным. Существует множество теологических интерпретаций этого перводвигателя, тип активности которого воплощает собой высшую форму наслаждения, заключающуюся в чистом созерцании самого себя как объекта – естественное состояние для божественных существ. Тогда логично предположить следующее: сколько бы ни оказалось причин для недоумений, у Аристотеля было все необходимое для того, чтобы разобраться в них. Некоторые поздние комментаторы утверждали, будто бы одного перводвигателя для самой удаленной сферы вполне достаточно для обеспечения работы системы. Тем не менее, как полагал Аристотель, скорее всего, каждое планетное движение по типу Евдокса обладает собственным перводвигателем, поэтому их общее число должно равняться 55 (или 47). Судя по всему, в итоге он соглашается признать их богами. В дальнейшем, в эпоху поздней Античности и в Средние века, те, кто находил эту идею неприемлемой, обычно предпочитали заменять их «духами» или ангелами.
От Симпликия мы узнаем, что система концентрических сфер продолжала изучаться и была воспринята Автоликом из Питаны, жившим около 300 г. до н. э. Автолик написал сочинения по «сферической астрономии», а именно по геометрии (небесных) сфер, и они пользовались широкой популярностью у арабов, иудеев и римлян вплоть до начала Средних веков; но эти работы не содержали теории, похожей на теорию Евдокса. Тем не менее Автолик защищал ее от нападок некоего Аристофера, оставшегося в истории в качестве учителя астронома-поэта Арата. Теорию признали несовершенной, поскольку она не могла объяснить изменение яркости планет. Симпликий полагает, что этот ее недостаток тревожил в том числе и Аристотеля.


