Алексей Лобанов
Энциклопедия финансового риск-менеджмента

Полная версия

1.27. Важнейшие виды случайных процессов

1.27.1. Случайное блуждание

Сечением случайного блуждания в момент времени t₀ + kh является дискретная случайная величина, закон распределения вероятностей которой имеет вид:

Траектории случайного блуждания изображены на рис. 1.29 (точками выделена одна из траекторий).

Случайное блуждание α (w, t) обладает независимыми приращениями, причем

1.27.2. Биномиальная модель

Случайный процесс β(w, t), определенный на множестве

называется биномиальной моделью (binominal model), если

Сечением биномиальной модели в момент времени t₀ + kh является дискретная случайная величина, закон распределения вероятностей которой имеет вид:

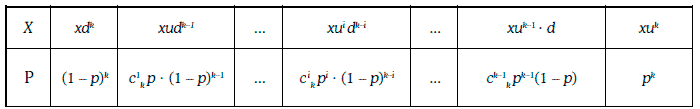
Траектории биноминальной модели изображены на рис. 1.30.

Если случайный процесс β (w, t) является биномиальной моделью с параметрами u, d, p, то

Приращения биномиальной модели, вообще говоря, не являются независимыми. Однако случайный процесс ln β (w, t) имеет независимые приращения.

Случайное блуждание и биноминальная модель относятся к случайным процессам с дискретным временем (discrete time process). Важнейшим примером случайного процесса с непрерывным временем (continuous time process) является винеровский случайный процесс.

1.27.3. Винеровский случайный процесс

Случайный процесс w(w, t), определенный на промежутке [t₀, +∞), называется винеровским случайным процессом (Wienerprocess), если выполняются следующие условия:

Для моделирования траекторий винеровского случайного процесса w (w, t) на заданном промежутке времени [t₀, Т] можно применить метод Монте-Карло.

Сам винеровский случайный процесс редко используется для моделирования финансовых показателей, так как имеет постоянное математическое ожидание. Однако на основе винеровского процесса строятся почти все случайные процессы, используемые в настоящее время для моделирования различных финансовых показателей.

1.28. Понятие о стохастических дифференциальных уравнениях

Стохастическим дифференциальным уравнением (stochastic differential equation) называется уравнение вида

Решением стохастического дифференциального уравнения (1.71) на промежутке [t, Т] называется случайный процесс х (w, τ), удовлетворяющий следующим условиям:

Любое решение стохастического дифференциального уравнения (1.71), удовлетворяющее некоторому начальному условию

В частности, геометрическим броуновским движением (geometric Brownian motion) является случайный процесс, удовлетворяющий стохастическому дифференциальному уравнению:

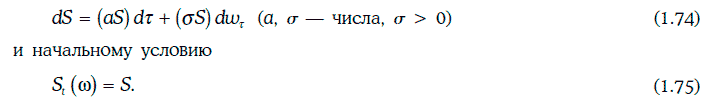
Геометрическое броуновское движение, определяемое условиями (1.74) и (1.75), можно найти в явном виде:

Свойства геометрического броуновского движения

Во многих случаях можно считать, что эволюция цены финансовых активов описывается геометрическим броуновским движением. Такое моделирование оказывается достаточно точным, например, в случае обыкновенных акций.

Пример 1.72. Инвестор считает, что цена бездивидендной акции описывается геометрическим броуновским движением с коэффициентом смещения 0,1 и годовой волатильностью 40 %. В данный момент времени цена акции равна 100 долл. Инвестора интересует цена этой акции через месяц.

Эволюцию цены В_τ облигации с нулевым купоном можно описывать с помощью геометрического броуновского движения, лишь когда до погашения облигации остается достаточно много времени. Действительно, в момент погашения Т ее цена всегда равна номиналу, т. е. известна достоверно. Это означает, что и зависимость от времени должна иметь вид, изображенный на рис. 1.31.

Таким образом, при моделировании эволюции цены облигации с нулевым купоном необходимо учитывать эффект приближения к номиналу (pull to par), а геометрическое броуновское движение этот эффект не учитывает, так как растет во времени линейно.

В общем случае найти решение стохастического дифференциального уравнения (1.71) в явном виде не удается. Поэтому для моделирования траекторий случайного процесса Ито часто применяется метод Монте-Карло.

Чтобы смоделировать траекторию случайного процесса Ито на отрезке [t, Т], этот отрезок разбивается на n равных частей (n должно быть большим), а затем разыгрывается случайная величина ξ, распределенная нормально с параметрами Тогда для последовательности случайных чисел δ₁, δ₂…., δ_n будет построена соответствующая последовательность значений случайной величины ξ, а траектория случайного процесса Ито будет определяться точками:

Указанным выше способом можно построить сколь угодно много траекторий случайного процесса Ито.

1.29. Основы теории экстремальных значений

Дана последовательность независимых одинаково распределенных случайных величин: η₁, η₂…., η_n…. с функцией распределения F(x).

Можно рассмотреть новую последовательность случайных величин {M_n}, где M_n = max {η₁, η₂…., η_n….}, n = 1, 2, 3…..

Функция распределения случайной величины M_n определяется следующим образом:

Теорема Фишера-Типпета

Дана последовательность независимых одинаково распределенных случайных величин η₁, η₂…., η_n…..

Следствие из теоремы Фишера – Типпета

Если случайные величины η₁, η₂, …, η_n независимы и одинаково распределены, а n достаточно велико, то функция распределения случайной величины M_n = max{η₁, η₂, …, η_n} практически совпадает с функцией обобщенного распределения экстремальных значений (при подходящем выборе параметров ξ, μ и σ).

Предположим, что случайная величина M_n = max{η₁, η₂, …, η_n} имеет распределение Фреше, т. е.

Тогда справедливы следующие утверждения:

1. Плотность распределения случайной величины M_n имеет следующий вид (рис. 1.32).

2. Математическое ожидание и дисперсии случайной величины M_n можно найти по формулам:

Параметры ξ, μ, σ можно подобрать на основе статистических данных.

Для измерений экстремальных событий может быть использовано распределение Парето (Pareto distribution), которое определяется функцией:

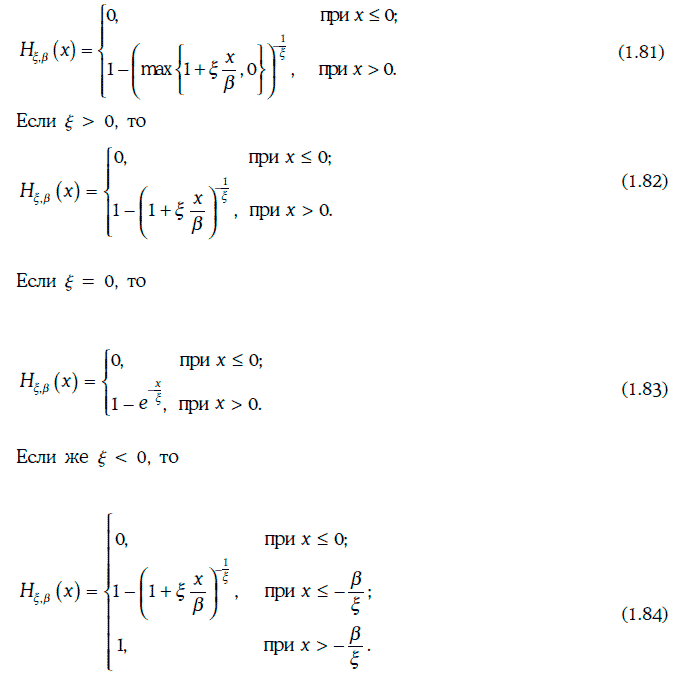
Для большого класса случайных величин η при достаточно большом пороговом значении u справедливо равенство:

Соотношение (1.85) позволяет оценивать «хвосты» распределений на основе статистических данных.

Литература

1. Барбаумов В. Е., Гладких И. М., Чуйко А. С. Финансовые инвестиции: Учебник. – М.: Финансы и статистика, 2003.

2. Доугерти К. Введение в эконометрику. – М.: ИНФРА-М, 2001.

3. Дуглас Л. Г. Анализ рисков операций с облигациями на рынке ценных бумаг. – М.: Филинъ, 1998.

4. Количественные методы финансового анализа / Под. ред. С. Дж. Брауна, М. П. Крицмена. – М.: ИНФРА-М, 1996.

5. Fabozzi F. J. Fixed income mathematics. 3rd ed. – N.Y.: McGraw-Hill, 1997.

6. Fabozzi F. J. (ed.) Advances in fixed income valuation, modeling and risk management. – Pennsylvania: Associates New Hope, 1997.

II. Производные финансовые инструменты
В. Е. Барбаумов

2.1. Введение

В настоящее время для идентификации и измерения рисков широко используется теория производных финансовых инструментов. Изучение производных финансовых инструментов важно еще и потому, что сами эти инструменты являются источниками рисков как для различных финансовых институтов, так и для финансового рынка в целом. Кроме того, производные финансовые инструменты – одно из важнейших средств хеджирования тех или иных рисков. Именно поэтому данная глава посвящена изучению производных финансовых инструментов.

В главе рассматриваются как простейшие производные финансовые инструменты – форвардные и фьючерсные контракты, свопы, так и более сложные – опционы различных видов и инструменты со встроенными опционами. Основное внимание уделяется методам оценки таких инструментов и основным направлениям их использования.

Важнейшими производными финансовыми инструментами являются классические европейские и американские опционы. Подробно рассматриваются методы оценки таких опционов в случае, когда стоимость исходных активов определяется геометрическим броуновским движением. В частности, приводятся формулы Блэка-Шоулза для оценки европейских опционов и разбирается их использование. Применение классических опционов для хеджирования основных финансовых рисков также рассматривается в данной главе.

В заключительной части главы обосновывается построение биномиальной модели процентной ставки и ее использование для оценки финансовых инструментов, производных от процентных ставок: кэпов, флоров, свопционов и облигаций со встроенными опционами. Кроме того, приводится обзор и других моделей временной структуры процентных ставок.

2.2. Форвардные контракты и их основные характеристики

В настоящее время на развитых финансовых рынках важную роль играют так называемые производные инструменты (derivatives). Простейшим из производных инструментов является форвардный контракт.

Форвардный контракт, или форвард (forward), представляет собой соглашение купить или продать некоторые активы, называемые «базисными» (underlying), в определенный момент времени в будущем по заранее установленной цене. Обычно форвардные контракты заключаются между финансовым институтом и одним из его корпоративных клиентов. Таким образом, в форвардном контракте всегда присутствуют две стороны. При этом говорят, что сторона, согласившаяся в будущем купить активы, занимает длинную позицию, а сторона, согласившаяся продать активы, – короткую.

Так как стороны форвардного контракта равноправны и подвержены одному и тому же риску, то при заключении форвардного контракта никто никому ничего не платит. Это означает, что в момент заключения форвардного контракта стоимость его равна нулю.

Цену, по которой стороны согласились купить (и соответственно продать) активы, называют ценой поставки активов (delivery price). Цену поставки обозначим через K. Момент времени, когда происходит покупка и продажа активов, называют датой исполнения форвардного контракта, или датой поставки. Момент исполнения форвардного контракта обозначим через Т.

В момент исполнения форвардного контракта доход (выигрыш) от той или иной позиции определяется в зависимости от цены поставки K и спот-цены активов S_T. Доход от длинной позиции в момент Т равен S_T – K, а от короткой позиции K – S_T (рис. 2.1 и 2.2).

В дальнейшем мы будем исходить из следующих предположений:

1. Рынки являются совершенными (perfect):

• отсутствуют транзакционные расходы и налоги;

• ни один инвестор, покупая или продавая активы, не может повлиять на цены;

• разрешены короткие продажи.

2. Участники рынка могут неограниченно кредитовать или занимать деньги под одну и ту же безрисковую ставку 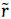(при непрерывном начислении).

3. По форвардным сделкам отсутствует кредитный риск.

4. Отсутствуют прибыльные арбитражные возможности, т. е. нельзя получить безрисковый доход за счет различия цен на активы.

При соблюдении этих условий все форвардные контракты на один и тот же вид активов с датой поставки Т будут в данный момент времени заключаться по одной и той же цене поставки.

Действительно, предположим, что в данный момент времени можно заключить форвардные контракты с ценами поставки К₁ и K₂, где K₁ > K₂.

Тогда можно занять короткую позицию по первому контракту и одновременно длинную позицию по второму контракту, при этом начальные затраты будут нулевыми. В момент Т исполнения контрактов будет получен доход K₁ – K₂ на каждую единицу активов. Так как отсутствуют прибыльные арбитражные возможности, то этого быть не может. В силу этого закона одной цены имеет смысл следующее определение:

Цена поставки, по которой в данный момент времени t заключаются форвардные контракты на данный вид активов с датой исполнения Т, называется форвардной ценой активов (forward price) на срок Т – t лет.

Итак, в начальный момент времени стоимость форвардного контракта равна нулю, так как в этот момент времени форвардная цена активов совпадает с ценой поставки этих активов. Однако через некоторое время форвардная цена активов может измениться, а цена поставки зафиксирована в контракте. Значит, после заключения форвардного контракта та или иная позиция по этому контракту может приобрести положительную или отрицательную стоимость. Эта величина показывает, что можно было бы получить, продав форвардный контракт, если бы существовал вторичный рынок для таких контрактов.

Если бы существовал вторичный рынок для форвардных контрактов, то стоимости длинной и короткой позиций в форвардном контракте определялись бы следующими равенствами:

где t – текущий момент времени (после заключения форвардного контракта);

Т – дата поставки;

K – цена поставки;

F – форвардная цена на момент t.

Докажем, например, равенство (2.1). Если

то займем сумму f_дл под безрисковую ставку на срок Т -1 лет, приобретем длинную позицию по форвардному контракту с ценой поставки K и займем короткую позицию по контракту с ценой поставки F. В момент времени Т будет получен безрисковый доход:

При отсутствии прибыльных арбитражных возможностей этого быть не может. Предположим теперь, что

В этом случае произведем короткую продажу длинной позиции по форвардному контракту с ценой поставки K, полученную денежную сумму f_дл инвестируем под ставку на Т- t лет и займем длинную позицию по форвардному контракту с ценой поставки F. В момент времени Т доход составит:

Так как этот доход, очевидно, является безрисковым, то и неравенство (2.4) выполняться не может. Значит,

Популярным видом форвардных контрактов является соглашение о форвардной процентной ставке (forward rate agreement – FRA).

Соглашение о форвардной процентной ставке – это контракт, устанавливающий на определенный будущий период процентную ставку для заемщика и кредитора.

Сторона, занимающая длинную позицию по FRA, обязана через Т₁ месяцев от текущего момента взять кредит размером L на срок Т₂ – Т₁ месяцев под контрактную процентную ставку f_k. Сторона, занимающая короткую позицию по FRA, обязана через Т₁ месяцев от текущего момента предоставить кредит размером L на срок Т₂ – Т₁ месяцев под контрактную процентную ставку f_k.

Замечание. Обычно разность Т₂ – Т₁, измеряемая в месяцах, является делителем 12, причем если 12/(Т₂ – Т₁) = m, то контрактная процентная ставка определяется при начислении m раз в году.

Выигрыш стороны с длинной позицией по FRA на момент Т₂ составляет:

где R – рыночная процентная ставка на момент Т₁.

В самом деле, взяв кредит размером L под контрактную процентную ставку f_k, можно полученную сумму инвестировать под рыночную ставку R. Тогда выигрыш на момент Т составит:

Пример 2.1. Длинная позиция по FRA эквивалентна следующей стратегии:

• взять кредит за 5 месяцев;

• инвестировать полученную сумму на 2 месяца.

Во многих случаях по условиям FRA фактического размещения денежных средств не производится, а расчеты производятся в момент времени Т₁.

В этом случае сторона с длинной позицией по FRA в момент Т₁ получает денежную сумму а сторона с короткой позицией ее платит.

При отсутствии арбитражных возможностей контрактная процентная ставка по FRA должна совпадать с предполагаемой форвардной процентной ставкой _Т1f_Т2.

Для доказательства рассмотрим следующие две стратегии:

2.3. Форвардная цена финансовых активов

Форвардная цена активов зависит от вида этих активов и от того, приносят ли эти активы доходы. В данном разделе мы рассмотрим, как оцениваются форвардные цены финансовых активов, т. е. таких, которые рассматриваются участниками рынка только как средство инвестирования, в отличие от товаров, которые участники рынка рассматривают как средство потребления.

В зависимости от того, приносят ли данные финансовые активы доходы или нет, мы будем рассматривать три различных случая. В каждом из этих случаев предполагается, что соблюдаются предположения о рынке 1-4, изложенные выше.

2.3.1. Форвардная цена активов, не приносящих доходов

Такими активами, например, являются облигации с нулевыми купонами и акции, по которым не выплачиваются дивиденды.

Покажем, что форвардная цена F таких активов определяется равенством:

где S – спот-цена активов в текущий момент времени t;

– безрисковая процентная ставка при непрерывном начислении по инвестициям на Т- t лет;

Т – дата поставки активов.

При рассматриваемой стратегии не требуется производить начальных затрат, и эта стратегия не содержит риска.

По условию на рынке отсутствуют прибыльные арбитражные возможности.

то можно произвести короткую продажу базисных активов, полученную денежную сумму инвестировать под безрисковую ставку на Т – t лет и занять длинную позицию по форвардному контракту на эти активы.

Тогда в момент поставки активов будет получен безрисковый доход

что противоречит нашим предположениям о рынке. Следовательно,

Стоимости длинной и короткой позиций по форвардному контракту на активы, не приносящие доходов, определяются равенствами:

Пример 2.2. Найдем форвардную цену акции, не приносящей дивидендов, с поставкой через 3 месяца, если текущая цена акции 40 долл., а безрисковая процентная ставка на 3 месяца равна 3 %.

В данном случае

Тогда

Если на рынке форвардная цена акции оказалась равной 42 долл., то возможна следующая прибыльная арбитражная стратегия: занять 40 долл. на 3 месяца под безрисковую ставку 3 %, купить на спот-рынке акцию и занять короткую позицию по форвардному контракту. В момент поставки акции будет получен доход:

2.3.2. Форвардная цена активов, приносящих известные доходы

Такими активами могут служить купонные облигации или акции с известными заранее дивидендами.

Форвардная цена F активов с известными доходами определяется равенством:

где S – спот-цена активов в текущий момент времени t;

I – приведенное значение доходов, поступающих от активов за время от t до Т;

Т – дата поставки активов.

Стоимости длинной и короткой позиций по форвардному контракту на активы с известными доходами можно найти следующим образом:

Пример 2.3. Найдем форвардную цену акции с поставкой через 8 месяцев, по которой дивиденды в размере 5 долл. ожидаются через 2 и 5 месяцев, если текущая цена акции равна 100 долл., а безрисковые процентные ставки на 2, 5 и 8 месяцев соответственно равны 5, 5,5 и 6 % (при непрерывном начислении процентов).

В данном случае

2.3.3. Форвардная цена активов, обладающих постоянной дивидендной доходностью

Предположим, что доходы от активов выплачиваются в виде самих этих активов, причем так, что за время τ единица активов с учетом накопленных доходов превращается в единиц активов. В этом случае говорят, что активы обладают постоянной дивидендной доходностью при непрерывном начислении.

Иностранную валюту можно рассматривать как актив с постоянной дивидендной доходностью. В самом деле, единицу иностранной валюты можно инвестировать под безрисковую ставку в той стране, где действует эта валюта. Тогда через т лет единица иностранной валюты превратится в единиц этой валюты. Таким образом, иностранная валюта обладает постоянной дивидендной доходностью, и эта дивидендная доходность совпадает с безрисковой процентной ставкой .

Во многих случаях фондовые индексы также можно рассматривать как активы с постоянной дивидендной доходностью.

Форвардная цена F активов с постоянной дивидендной доходностью при непрерывном начислении может быть найдена по формуле:

В этом случае для стоимости длинной и короткой позиций по форвардному контракту имеем равенства:

Пример 2.4. Найдем 8-месячную форвардную цену английского фунта стерлингов, если текущий обменный курс равен 1,8 долл. за фунт, а безрисковые процентные ставки в США и в Англии при непрерывном начислении процентов равны 6 и 4 % соответственно.

2.4. Форвардная цена товаров

Пусть F – форвардная цена некоторого товара в момент времени t с датой поставки Т.

Покажем, что при отсутствии прибыльных арбитражных возможностей справедливо неравенство

Так как данная стратегия не требует никаких начальных затрат и не содержит риска, то это – прибыльная арбитражная стратегия. Следовательно,

Выясним теперь, существует ли прибыльная арбитражная стратегия, если

Для получения безрискового дохода необходимо произвести короткую продажу единицы товара. Однако, если этот товар большинством инвесторов используется для потребления или в производстве, сделать это без дополнительных затрат невозможно.

Если же товар в основном используется как средство инвестирования, то возможна следующая стратегия: произвести короткую продажу единицы товара, экономя при этом затраты на хранение товара, полученные средства инвестировать под безрисковую процентную ставку на Т – t лет и занять длинную позицию по форвардному контракту.

В момент Т будет получен доход

Таким образом, если товар используется в основном как средство инвестирования, а не потребления, то

Отметим, что к товарам, являющимся средством инвестирования, относятся, например, драгоценные металлы: золото, серебро, платина. Если же товар в основном используется как средство потребления, то

которое можно интерпретировать как меру физической полезности данного товара.

Пример 2.5. Найдем 10-месячную форвардную цену унции серебра, если текущая цена унции серебра равна 9 долл., затраты на хранение (охрану) составляют 0,24 долл. и выплачиваются поквартально вперед, а безрисковая процентная ставка для всех сроков при непрерывном начислении процентов составляет 10 %.

Пример 2.6. Оценим 9-месячную меру физической полезности одного барреля сырой нефти, если текущая цена барреля нефти равна 20,00 долл., затраты на хранение барреля нефти равны 0,5 долл. и оплачиваются в конце срока хранения, 9-месячная форвардная цена барреля нефти составляет 20,20 долл., а безрисковая процентная ставка на 9 месяцев при непрерывном начислении равна 8 %.

В данном случае

Значит, для определения физической полезности барреля нефти имеем уравнение:

Таким образом, 9-месячная мера физической полезности барреля сырой нефти составляет 9,77 %.