Алексей Лобанов
Энциклопедия финансового риск-менеджмента

Полная версия

Изменения во втором издании

Во втором, исправленном и дополненном издании книги улучшения были внесены практически во все главы, при этом материал глав II, VIII, IX и X был существенно расширен. Так, в главе II более подробно освещены арбитражные и неарбитражные модели эволюции процентной ставки и методы ценообразования инструментов, производных от процентной ставки, в частности опционов на купонные облигации. В главе V приведена полная классификация событий, приводящих к операционным потерям, которая была предложена Базельским комитетом по банковскому надзору в Новом соглашении по капиталу. Глава VIII дополнена материалами по организационным аспектам риск-менеджмента, в том числе по построению «карты рисков»; также в ней приведены рекомендации Базельского комитета по проведению стресс-тестирования в рамках подхода на основе внутренних рейтингов. В главу IX добавлен раздел, посвященный рискам страхования банковских вкладов. Глава X расширена за счет включения нового раздела, посвященного анализу макроэкономических рисков как причин банковского кризиса в России в 1998 г.

Изменения в четвертом издании

В четвертом, исправленном и дополненном издании в главу I включены определения медианы и моды вероятностных распределений, характеристики биномиального распределения, распределения Пуассона, бета- и гамма-распределений, двумерного нормального распределения. Глава также дополнена разделом, посвященным теории экстремальных значений. В главе II приведена краткая характеристика соглашений о форвардной процентной ставке (FRA). В главу VIII включены новые комментарии к методу RAROC и его модификациям, описания актуальных сценариев для проведения стресс-тестирования, а также раздел, посвященный методам контроля за трейдерами и управлению торговыми лимитами. В главе IX полностью переработан и дополнен обзор Нового соглашения по капиталу 2004 г. («Базеля II»), выполненный на основе последней редакции этого соглашения от ноября 2006 г. Кроме того, существенно обновлена библиография глав VIII и IX.

Редакторы и авторы выражают благодарность всем читателям, приславшим свои отзывы и замечания к текстам предыдущих изданий книги.

А. А. Лобанов, А. В. Чугунов

Исследовательская группа «РЭА – Риск-Менеджмент»

I. Количественный анализ
В. Е. Барбаумов

1.1. Введение

Научно обоснованное управление финансовыми рисками невозможно без соответствующей методики измерения этих рисков. Существующие методы измерения финансовых рисков в основном опираются на современную теорию финансовых инструментов с фиксированными доходами, теорию вероятностей, математическую статистику и теорию случайных процессов. Именно эти вопросы составляют основное содержание первой главы настоящей книги.

В частности, при изучении финансовых инструментов с фиксированными доходами вводятся многие фундаментальные понятия теории финансов: будущая и приведенная стоимости инвестиций, внутренняя доходность облигаций, временная структура процентных ставок, кривая рыночных доходностей, дюрация и выпуклость портфелей облигаций. Все эти понятия широко используются как при измерении финансовых рисков, так и при построении стратегий хеджирования этих рисков.

После небольшого обзора основных положений теории вероятностей рассматриваются важнейшие статистические методы оценки различных финансовых показателей, используемых в риск-анализе.

В заключительной части главы вводятся основополагающие понятия теории случайных процессов: сечения и траектории, математическое ожидание и дисперсия, процесс случайного блуждания, биномиальная модель, винеровский случайный процесс, стохастические дифференциальные уравнения. Подробно исследуется процесс геометрического броуновского движения, который играет ключевую роль в оценке производных финансовых инструментов.

1.2. Будущая стоимость денежного потока

Предположим, что денежная сумма Р инвестирована на Т лет под годовую процентную ставку r(m) при начислении процентов m раз в год. Тогда будущая стоимость (future value) инвестиции может быть найдена следующим образом:

Если же денежная сумма Р инвестирована под годовую процентную ставку при непрерывном начислении процентов, то будущая стоимость инвестиции определяется равенством:

Пример 1.1. Денежная сумма в 1 млн долл. инвестирована на 6 лет под годовую процентную ставку 6,4 %. Определим будущую стоимость инвестиции, если проценты начисляются: а) один раз в год; б) дважды в год; в) ежеквартально; г) непрерывно:

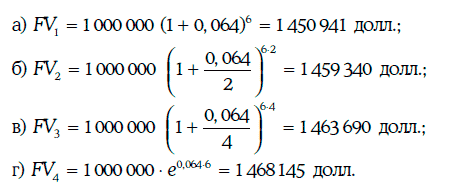
Очевидно, что будущая стоимость инвестиции возрастает при:

а) увеличении срока;

б) возрастании годовой процентной ставки;

в) росте частоты начисления процентов.

Годовые процентные ставки называют эквивалентными, если при инвестировании любой суммы Р под эти ставки на один и тот же срок совпадают будущие стоимости.

В частности, годовые процентные ставки r(m) и r(n) при начислении процентов m и n раз соответственно оказываются эквивалентными тогда и только тогда, когда

Годовая процентная ставка 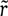при непрерывном начислении процентов эквивалентна годовой процентной ставке r(m) при начислении процентов m раз в год тогда и только тогда, когда

Пример 1.2. Банк предлагает по депозитам годовую процентную ставку в 8 % при начислении процентов один раз в год. Какую годовую процентную ставку можно требовать при начислении процентов: а) дважды в год; б) ежеквартально; в) непрерывно?

Предположим теперь, что инвестору обещают через t₁, t₂…., t_n лет денежные суммы P_t1, P_t2…., P_tn соответственно. Если инвестор предполагает инвестировать все поступающие денежные суммы под одну и ту же годовую процентную ставку, то через Т лет будущая стоимость денежного потока будет равна:

Какова будущая стоимость денежного потока через 3 года, если инвестор предполагает инвестировать поступающие денежные суммы под 7 % при начислении процентов: а) дважды в год; б) непрерывно?

Если одну и ту же денежную сумму выплачивают (или получают) периодически в течение ряда лет, то соответствующий денежный поток называют рентой^[13] (annuity). Промежуток времени между двумя соседними платежами – это рентный период. Ренту называют обыкновенной (ordinary annuity), если первый рентный платеж приходится в точности на конец одного рентного периода.

Рассмотрим обыкновенную ренту размером А сроком на Т лет, рентный период которой составляет 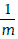года. По данной ренте будут произведены Тт платежей одной и той же величины А, причем i-й платеж (i = 1, 2…., Тт) должен быть произведен через  лет.

Если предположить, что все рентные платежи будут инвестироваться под одну и ту же годовую процентную ставку r(m) при начислении процентов m раз в год, то будущая стоимость обыкновенной ренты через Т лет может быть определена следующим образом:

Так как

то

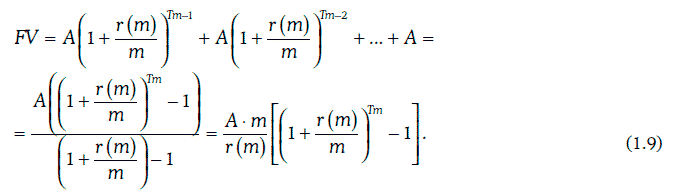
Пример 1.4. Менеджер покупает облигацию, по которой выплачиваются проценты в размере 40 долл. каждые полгода в течение 10 лет и номинальная стоимость в 1000 долл. в конце десятого года. Определим будущую стоимость инвестиции через 10 лет, если все платежи реинвестируются под 6,7 %, а первый процентный платеж производится через 6 месяцев.

Денежный поток, определяемый облигацией, представляет собой обыкновенную ренту, в которой А = 40 долл., m = 2, Т = 10 лет, и выплату 1000 долл. в конце десятого года. Отсюда

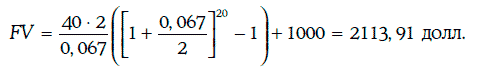
1.3. Приведенная стоимость денежного потока

Денежную сумму, которую необходимо инвестировать сегодня, чтобы через определенное время получить данную будущую стоимость, называют приведенной стоимостью (present value).

Имеет место следующее равенство:

где

РV – приведенная стоимость инвестиции;

FV – будущая стоимость;

Т – срок инвестиции;

r(m) – процентная ставка при начислении процентов m раз в год.

Процентную ставку r(m), используемую для определения приведенной стоимости инвестиции, называют ставкой дисконтирования (discount rate). Если ставка дисконтирования определяется при непрерывном начислении процентов, то формула (1.10) принимает вид:

Пример 1.5. Менеджер пенсионного фонда должен через 6 лет выплатить 10 млн долл. В данный момент менеджер имеет возможность инвестировать любую сумму под 7,5 % при начислении процентов дважды в год. Сколько должен инвестировать менеджер пенсионного фонда, чтобы выполнить свое обязательство?

Приведенная стоимость 10 млн долл. может быть найдена по формуле (1.10):

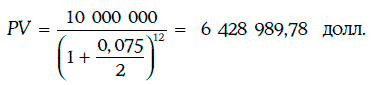
Следовательно, менеджер должен инвестировать 6 428 989,78 долл., чтобы через 6 лет получить 10 млн долл.

Из равенства (1.10) следует, что при прочих равных условиях:

1) чем больше ставка дисконтирования, тем меньше приведенная стоимость, и наоборот;

2) чем меньше срок инвестиции, тем больше приведенная стоимость, и наоборот.

Приведенная стоимость потока денежных платежей определяется в виде суммы приведенных стоимостей платежей, образующих этот денежный поток.

Пример 1.6. Финансовый директор компании знает, что ему предстоит произвести следующие платежи:

Какую денежную сумму необходимо инвестировать сегодня, чтобы обеспечить выполнение обязательств, если процентная ставка равна 6 % при начислении процентов дважды в год?

Достаточно определить приведенную стоимость данного потока платежей:

Если денежный поток представляет собой обыкновенную ренту, по которой т раз в год в течение Т лет выплачивается одна и та же денежная сумма А, то приведенная стоимость такой ренты может быть найдена следующим образом:

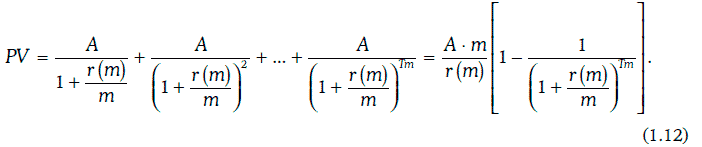
Пример 1.7. Банк согласился предоставить 30-летний ипотечный кредит в размере 100 000 долл. По условиям ипотечного кредитования ежемесячные платежи заемщика должны быть одинаковыми. Годовая процентная ставка, требуемая банком, равна 12 %. Какова величина ежемесячного платежа заемщика?

Величина ежемесячного платежа заемщика определяется из условия, что приведенная стоимость потока платежей заемщика должна составить 100 000 долл. Значит,

Обыкновенную ренту называют бессрочной^[14] (perpetual annuity), если поток рентных платежей не ограничен по времени. Приведенная стоимость бессрочной ренты, по которой m раз в год выплачивается сумма А, может быть найдена следующим образом:

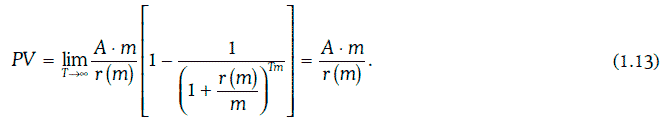
1.4. Внутренняя доходность финансовых инструментов

Внутренней доходностью (internal rate of return – IRR) финансового инструмента называют процентную ставку, при которой приведенная стоимость потока платежей по данному финансовому инструменту совпадает с его рыночной ценой.

Пример 1.8. Финансовый инструмент продается по цене 1243,82 долл., и по нему каждые 6 месяцев выплачивается по 50 долл. в течение 5 лет и еще 1000 долл. в конце пятого года. Покажем, что внутренняя доходность данного финансового инструмента при начислении процентов дважды в год составляет 4,5 %.

Приведенная стоимость денежного потока по данному финансовому инструменту определяется следующим образом:

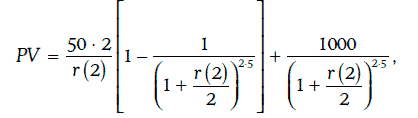
где r(2) – годовая процентная ставка при начислении процентов дважды в год.

При r(2) = 0,045 имеем

Так как приведенная стоимость денежного потока, определяемого финансовым инструментом, совпала с его рыночной ценой, то внутренняя доходность этого инструмента действительно равна 4,5 %.

Рассмотрим финансовый инструмент со следующим потоком платежей:

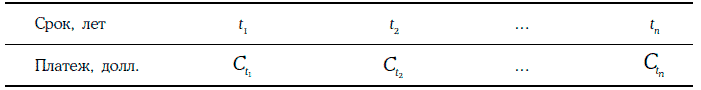
Внутренняя доходность рассматриваемого финансового инструмента при начислении процентов m раз в год является решением уравнения:

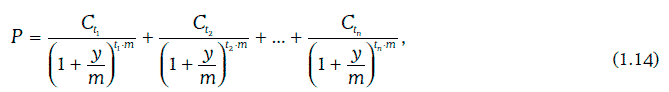
где Р – рыночная цена финансового инструмента.

Функция стоящая в правой части уравнения (1.14), всегда является убывающей и выпуклой. График функции изображен на рис. 1.1.

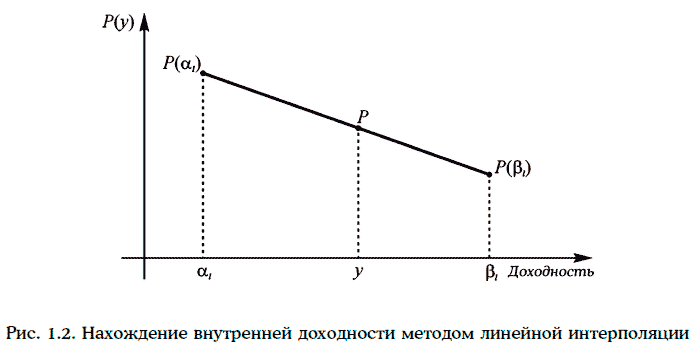
Для решения уравнения (1.14) можно использовать метод проб и ошибок. Вначале найдем простым подбором числа α₁ и β₁ так, чтобы P(α₁) > Р, а P(β₁) < Р (рис. 1.2). Тогда искомая внутренняя доходность будет находиться между α₁ и β₁, т. е. у ∈ (α₁, β₁). Промежуток (α₁, β₁) разделим на 10 равных частей. И, вычисляя значение функции Р(у) в точках деления, найдем числа α₂ и β₂ так, чтобы:

Тогда у ∈ (α₂, β₂). Повторяя данную процедуру несколько раз, можно найти достаточно малый промежуток (α₁, β₁), на котором находится искомая внутренняя доходность. В этом случае искомую внутреннюю доходность можно определить на основе линейной интерполяции:

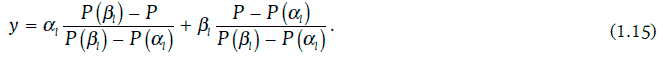
Определим внутреннюю доходность финансового инструмента при начислении процентов дважды в год, если рыночная цена финансового инструмента равна 7000 долл.

Чтобы определить искомую внутреннюю доходность, достаточно решить уравнение:

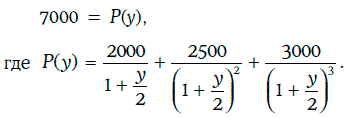
Так как

то полагаем α₁ = 0,06, β₁ = 0,07. Промежуток (α₁, β₁) разделим на 10 равных частей:

Заметим, что P(0,066) = 7000,5057 > 7000; P(0,067) = 6993,3546 < 7000. Значит, можно считать, что α₂ = 0,066, а β₂ = 0,067.

Используя линейную интерполяцию, получим, что

Так как Р(0,06607) = 7000,005, то искомая внутренняя доходность составляет 6,607 %.

Если по данному финансовому инструменту приходится только один платеж, то его внутренняя доходность при начислении процентов m раз в год может быть найдена по формуле:

где С – размер платежа по финансовому инструменту;

Р – рыночная цена финансового инструмента;

Т – срок платежа по финансовому инструменту.

1.5. Котируемая цена купонных облигаций

Купонной облигацией (coupon bond) называют финансовый инструмент, по которому периодически выплачиваются купонные проценты вплоть до погашения и номинальная стоимость в момент его погашения.

Отношение суммы купонных платежей за год к номинальной стоимости облигации называют купонной ставкой облигации (coupon rate).

Если f – купонная ставка облигации, то размер одного купонного платежа может быть найден по формуле:

где q – размер купонного платежа;

А – номинальная стоимость облигации;

m – количество купонных выплат за год.

Пример 1.10. Дана 9 %-ная купонная облигация с полугодовыми купонами и номинальной стоимостью 1000 долл. Определим поток платежей по облигации, когда до ее погашения остается 2,25 года.

В данном случае f = 0,09, А = 1000 долл., m = 2. Значит,

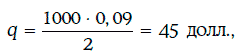
и поток платежей по облигации имеет вид:

Цена купонной облигации должна совпадать с приведенной стоимостью потока платежей, обещаемых по этой облигации. Чтобы определить приведенную стоимость потока платежей, необходимо знать ставку дисконтирования, которая в данном случае является требуемой доходностью (required yield).

Требуемая доходность для данной купонной облигации устанавливается на основе исследования внутренних доходностей финансовых инструментов, сравнимых с данной купонной облигацией. При этом учитываются такие факторы, как кредитный рейтинг эмитентов, ликвидность финансовых инструментов и т. д.

Котируемая цена (clean price) купонных облигаций определяется в моменты времени, когда происходят выплаты очередных купонных платежей. Котируемая цена купонной облигации с полугодовыми купонами может быть найдена по формуле:

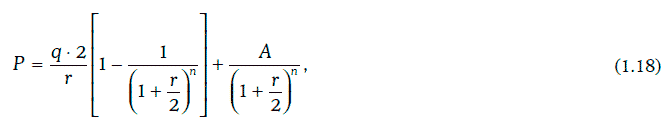
где P – котируемая цена облигаций;

– размер одного купонного платежа;

r – требуемая доходность;

А – номинальная стоимость облигации;

n – количество купонных платежей, остающихся до погашения облигации.

Пример 1.11. Найдем цену 9 %-ной купонной облигации, номинальной стоимостью 1000 долл., когда до ее погашения остается 20 лет, а требуемая доходность составляет 8 %.

В данном случае A = 1000 долл., f = 0,09, 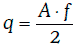= 45 долл., n = 40, r = 0,08.

Котируемую цену облигации можно найти по формуле (1.18):

Говорят, что купонная облигация продается по номиналу (par value), если ее котируемая цена совпадает с номинальной стоимостью. Купонная облигация продается по номиналу тогда и только тогда, когда купонная ставка облигации равна требуемой доходности.

Облигация продается с премией (at a premium), если ее котируемая цена выше номинальной стоимости. Купонная облигация продается с премией тогда и только тогда, когда купонная ставка выше требуемой доходности. Размер премии для облигаций с полугодовыми купонами составляет:

Говорят, что купонная облигация продается с дисконтом (at a discount), если ее котируемая цена ниже номинала. Облигация продается с дисконтом тогда и только тогда, когда купонная ставка облигации меньше требуемой доходности. Размер дисконта можно найти следующим образом:

Пример 1.12. Облигация из примера 1.11 продается с премией, так как ее купонная ставка f = 0,09 выше требуемой доходности r = 0,08. Размер премии можно определить по формуле (1.19):

Если с течением времени требуемая доходность не изменяется, то чем ближе дата погашения облигации, тем меньше размер премии (дисконта).

Зависимость котируемой цены облигации от количества купонных платежей, остающихся до погашения облигации, показана на рис. 1.3.

Котировкой облигации называют отношение

где Р – котируемая цена облигации;

А – номинальная стоимость облигации.

Зная котировку облигации и ее номинальную стоимость, можно найти котируемую цену облигации.

Пример 1.13. Если котировка облигации номинальной стоимостью 5000 долл. равна то ее котируемая цена равна

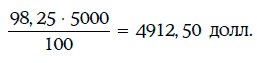
1.6. Цена купонных облигаций

Рассмотрим некоторую облигацию с полугодовыми купонами. Будем считать, что требуемая доходность известна и равна r.

Если расчетная дата приходится на дату купонного платежа, то цена облигации считается равной ее котируемой цене и может быть найдена по формуле (1.18). Если же расчетная дата находится между датами купонных платежей, то цена облигации определяется следующим образом:

где Р – цена облигации;

q – полугодовой купонный платеж;

А – номинальная стоимость облигации;

n – число купонных платежей, остающихся до погашения облигации;

w – отношение числа дней от расчетной даты до очередного купонного платежа к числу дней в купонном периоде.

Формулу (1.21) можно записать и в ином виде:

Пример 1.14. Дана 10 %-ная облигация с полугодовыми купонами номиналом 100 долл., погашаемая 1 марта 2003 г. Определим, какова была цена этой облигации 17 июля 1997 г. при требуемой доходности в 7 %.

В данном случае А = 100 долл., q = 5 долл., r = 0,07, n = 12.

При расчете фактического числа дней между двумя датами принято учитывать только одну из этих дат. Тогда число дней между 1 марта и 1 сентября 1997 г. – 184, а между 17 июля и 1 сентября 1997 г. – 46. Значит,

По формуле (1.22) найдем, что

Замечание. В примере 1.14 мы определяли число дней между двумя датами по календарю. Так принято, в частности, на рынке казначейских облигаций США. Этот стандарт расчета числа дней обозначают Actual/Actual. На других рынках облигаций могут использоваться и другие стандарты. Например, стандарт 30/360, когда число дней в любом месяце считается равным 30, а число дней в году – 360.

Пример 1.15. Определим цену облигаций из примера 1.14, если на рынке действует стандарт 30/360.

При стандарте 30/360 число дней между 1 марта и 1 сентября считается равным 180, а между 17 июля и 1 сентября – 44. Тогда

В этом случае цена облигации находится следующим образом:

Если покупка облигации производится на бирже, то покупатель обязан уплатить котируемую цену облигации и накопленные проценты (accrued interest), которые рассчитываются следующим образом:

где q – полугодовой купонный платеж;

N₁ – число дней от последнего купонного платежа до расчетной даты;

N – число дней в купонном периоде.

Сумму котируемой цены облигации и накопленных процентов называют «грязной» ценой (dirty price).

Пример 1.16. Определим величину накопленных процентов для облигации из примера 1.14.

При использовании стандарта Actual/Actual имеем:

а при стандарте 30/360:

1.7. Оценка доходности облигаций

На рынках облигаций используются различные меры доходности облигаций.

1.7.1. Текущая доходность

Текущей доходностью (currentyield) купонной облигации принято считать отношение суммы купонных платежей за год к рыночной цене облигации.

Пример 1.17. Определим текущую доходность 6 %-ной облигации с полугодовыми купонами номиналом 1000 долл., продающейся по цене 700,89 долл., когда до ее погашения остается 18 лет.

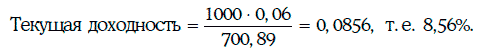
1.7.2. Доходность к погашению

Доходность к погашению (yield to maturity) облигации с полугодовыми купонами является решением уравнения:

где Р – котируемая цена облигации;

AI – накопленные проценты на расчетную дату;

q – полугодовой купонный платеж;

А – номинальная стоимость облигации;

n – число купонных платежей, остающихся до погашения облигации;

w – отношение числа дней между расчетной датой и очередным купонным платежом к числу дней в купонном периоде.

Пример 1.18. Найдем доходность к погашению облигации из примера 1.17.

В данном случае

Следовательно, доходность к погашению удовлетворяет уравнению:

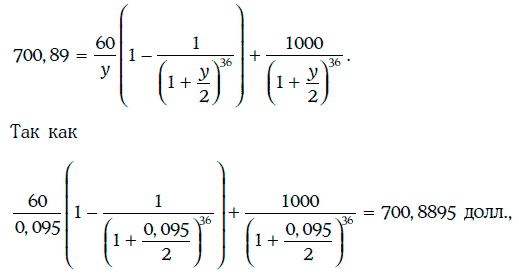
то доходность к погашению облигации равна 9,50 %.

Нетрудно убедиться, что имеют место следующие утверждения:

1) если купонная облигация продается по номиналу, то купонная ставка равна текущей доходности облигации и ее доходности к погашению;

2) если купонная облигация продается с премией, то ее купонная ставка больше текущей доходности, которая, в свою очередь, больше доходности к погашению;

3) если же купонная облигация продается с дисконтом, то ее купонная ставка меньше текущей доходности, которая, в свою очередь, меньше доходности к погашению (см. примеры 1.17 и 1.18).