
Иван Деревянко
Математика нуждается в систематизации
Тем не менее, именно Ленин беспощадно громил авторов четвертого измерения пространства. Но делал он это, как теперь выясняется совершенно напрасно, ибо как раз четвертого геометрического измерения не хватает для исчерпывающего представления, например, о форме (кроме трех габаритных размеров необходимо еще иметь структурный параметр, который в простейшем случае может быть представлен толщиной стенки или размером внутренней полости).
В защиту четвертого измерения свидетельствует тот факт, что замкнутые кривые, с внутренними петлями, представленные одним уравнением в одной системе координат могут быть получены сравнительно простыми средствами, если это уравнение имеет четвертую степень. Еще более убедителен этот факт, если таких замкнутых кривых, похожих друг на друга, надо иметь не одну, а несколько (в случае со строением атома это имеет принципиальное значение).
Для самых придирчивых математиков мы попытаемся соблюсти логическую строгость и показать, что всякая система, в т. ч. система исходных понятий, может быть названа системой, если она имеет четыре элемента (необходимое, но не достаточное условие). Пока мы ограничимся констатацией фактов и абстрагированием посредством аналогий.
Так математика всегда обходилась четырьмя простейшими арифметическими действиями: сложением, умножением, вычитанием и делением, но применяться эти действия надо именно в такой последовательности. В теории групп оказывается достаточным иметь исходное множество, операции над ее элементами, единичный и обратный элементы. Этот перечень можно продолжать, но из математики примеров уже достаточно.
Для большей убедительности можно привести еще один пример, но уже из области техники. Ни одна автоматическая система не будет работоспособной, если она не будет иметь необходимый минимум элементов: объект управления, датчик, задатчик и исполнительный орган. Отсутствие любого из элементов делает систему бессмысленной. Таким образом, можно констатировать, что набор неопределимых понятий должен состоять из 4-х исходных категорий. Если известно их число, то, руководствуясь принципом симметрии, о котором шла речь выше, не составляет большой проблемы выбор самих категорий.
В философии помогает сделать такой выбор гегелевские парные понятия неопределенного и определенного качества и количества, из которых получается система: свойство, качество, мера, количество. Этот выбор можно проиллюстрировать на самом простом примере: любой товар имеет название, качество, единицу измерения (меру), и число единиц (количество). В математике это будут: отображение множества, само множество, свойства элементов и область существования. В этой системе понятий центральное место принадлежит "мере", которая должна отображать некоторые константы в реальном мире.
Кроме единиц измерения, роль постоянства которых известна всем с младенчества, существуют еще жизненно важные константы, относительно которых можно оценивать качественные состояния объектов независимо от их природы с целью их сопоставления. Примером может служить предел существования в биологии, предел прочности в механике, предел сохранения целостности (неразрывности) в физике и т. д.
Но предел – это то, чего нельзя превысить. А есть, так называемые, узловые точки, при переходе через которые меняется либо знак, либо состояние, либо вид. Здесь, как нигде более, очень важно сопоставить понятие констант, разных по своей природе, и найти соответствующие зависимости.
Заблуждения академика Кашина Б.С.
В интернете опубликована статья: "С этой властью – тупик" – академик Борис Кашин. В статье сделана подборка высказываний академика Российской академии наук, профессора Бориса Сергеевича Кашина о президенте Путине, сложившейся при нём системе власти и о катастрофическом положении дел в нашей науке. Редакция спрашивает: «А что вы, уважаемые читатели, думаете по этому поводу?» Вот что автор книги думает по этому поводу.
Конечно, положение дел в науке если не катастрофическое, то, во всяком случае, далекое от нормального состояния. Но… Во-первых, не во всей науке, а, во-вторых, не только Путин за это ответственен.
Во-вторых, речь должна идти не о тех научных работниках, которые в большинстве своем не удостоены академических званий, но верой и правдой служат науке и создают уникальные технические системы.
Речь должна идти, главным образом, об Академии Наук России, прежде всего о тех ее членах, кто когда-то сделал что-то хорошее и получил за это соответствующие пожизненные блага. Бывает, что отец «протолкнет» туда сына или еще каким-нибудь нехорошим способом человек туда попадает. Но все-таки туда попадают за что-то.
Ну а дальше, став академиками, получают немалые привилегии и денежные вознаграждения не за результаты работы, а за звания, которые являются моральным поощрением, а не материальным.
Раньше в отраслевых институтах неостепененные сотрудники на различных должностях имели оклады примерно в два раза меньшие, чем у остепененных. Это был отличный стимул повышать квалификацию ученых. Специально за степени и, тем более звания никто ничего не платил. Академикам платят, непонятно за что.
Они возомнили себя носителями истины в последней инстанции и решили, что схватили черта за бороду. Им можно изрекать непогрешимое мнение, которое нельзя критиковать и излагать что-либо, отличное от их мнения.
Но не надо бы забывать о том, что академик тоже человек и он может ошибаться, тем более не в тех областях, где он преуспел. Короче говоря, создается каста «неприкасаемых», где можно материализовать пространство и время, придумывать виртуальные кванты и оболванивать народ прочими сказками. Вот, дескать, мы это знаем, а Вам, дуракам, знать не обязательно. Вы должны в это поверить.
А чтобы неповадно было не верить, создается комиссия по лженауке и прочие запретительные органы. Кто-нибудь может напечатать в академических или институтских изданиях что-нибудь даже слегка отличное от политики организации? Редакционная коллегия не пропустит.
А ведь печатные издания для того и создаются, чтобы учесть разные мнения на проблему. К тому же, печатные издания должны быть независимыми. Редакция может поинтересоваться мнением авторитетной организации или маститого академика, но решение принимать она должна самостоятельно.
Автор книги только слегка прокомментировал статью академика Глазьева, как его комментарий был немедленно удален с его, и ему запретили вообще заходить на сайт и что-нибудь писать или комментировать на этом сайте.
Автор подумал, что это сделали сотрудники сайта – сторонники академика, и написал ему лично письмо с просьбой хотя бы прочесть статью. Наверняка прочитал, но не ответил. Излюбленный способ, замолчать проблему, если ее решение противоречит твоей точке зрения. Как будто проблемы не существует. Глухое молчание. Что, в этом Путин виноват?
Такое впечатление, что лукавит академик Кашин. Он и решился на резкую критику Путина, очевидно, потому что увидел угрозу своему положению. Говоря о Путине и системе управления страной, которая сложилась при нём, академик утверждает, что «Президент отгородился от народа и даже от парламента, который не может ему задать ни одного вопроса. Он произвольно принимает решения, многие из которых противоречат общественным и государственным интересам».
Ну, во-первых, не столько Путин «отгородился» от народа, сколько его «отгородила» бюрократическая машина, которая исправно и вовсю работает и в Администрации Президента, и в Правительстве, и а Академии Наук, и во всех других государственных органах. Основой этой машины является чиновник, который, попав на тепленькое место, не хочет рисковать и что-то предпринимать, отличное от того, что хочет начальник, от которого зависит его карьера. И решение о допуске обращения к своему высшему руководителю принимает не специалист, а какой-нибудь клерк типа консультанта, который ничего не понимает в проблеме.
Во-вторых, если, получив письмо, нельзя его замолчать (некоторые организации создают специальные средства контроля), делается отписка со ссылкой на какие-нибудь законы. Из этой отписки следует, что ты сам виноват, неправильно написал, типа ты дурак, а мы белые и пушистые, нам закон не позволяет сделать то, что Вы предлагаете. А кто этот закон писал? Ну а, если отписаться нельзя, письмо отсылается в нижестоящие или другие организации, которые не имеют полномочий решать поднимаемую проблему. На собственном опыте автор убедился в этом.
В-третьих, какие еще можно принимать решения Президенту, если Кудрин ему говорит одно, Глазьев – другое, Белозеров – третье, а институт экономики РАН, вместо разработки моделей на основе всеобщих закономерностей, занимается всем, чем угодно, только не фундаментальными проблемами экономики. Там спорит о том, кто, когда и что сказал, участвуя во всяких гайдаровских чтениях и прочей ерунде.
Конкретный пример. Руководство международного комитета по стандартизации направило в институт экономики РАН статью автора книги о технологической эксплуатации с просьбой дать заключение. Глухое молчание. Не сами ли академики виноваты в «неправильных» решениях Президента?
Почему, например, в свое время целая когорта академиков так и не разработала программу "500 дней"? Почему академик Абалкин, так активно критиковавший экономику, в роли заместителя Председателя Правительства так ничего и не смог с ней сделать? Показателен в этом плане и научный доклад РАН «О стратегии развития экономики России.»
Удивительное дело, рядовой кандидат технических наук знает, что экономика – это такая же, как и все, система и должна работать точно так же, имея все элементы, присущие системам. А академики этого не знают, и создают экономические системы, которые не работают. Непростительно Вам, господа академики.
Поэтому Путин и вынужден сам принимать решения по своему уразумению. Организатор он хороший, а экономических и других специальных знаний не хватает, и ему никто ничего дельного предложить не может.
Академик считает, что
"…Последние изменения, внесенные в конституцию, сделали и без того чрезмерную власть президента абсолютной. Его окружение остается на плаву независимо от результатов своей деятельности…"
Да, это, в какой-то мере, так. Но при российской расхлябанности и вольнодумстве чиновников это неизбежно, нужна сильная центральная власть. Что касается окружения, возможно, что-то имеет место, но посмотрите, как он умеет подбирать кадры. Только Шойгу с Лавровым чего стоят. К тому же он вынужден применять политику противовесов опять-таки потому, что никто не может ему сказать, а как надо. Академики не создали сбалансированной модели.
С нынешней властью в стране наука находится в тупике, говорит академик. Дескать "Дела в науке развиваются от плохого к худшему. Перспективы при нынешней политике абсолютно не видно. Власть завела науку в тупик"
Да, это тоже так. Но не только власть это сделала, а сами академики ей помогли. Взять, хотя бы то, что изложено в статье автора книги «Смею возразить академику Александрову». Кроме того, в своем письме Президенту РАН автор подробно описал, что делается в Российской науке системным принципам вопреки. Глухое молчание.
Академик говорит о политике вредительства в отношении науки со стороны российских властей:
"…Если мы посмотрим науку, у нас идёт деятельность, которую надо самым внимательным образом спецслужбам изучить на предмет вредительства."
Все с точностью до наоборот. Вот уж, действительно, надо разбираться не только с чиновниками, но и с вредной деятельностью некоторых академиков. Не зря еще Пуанкаре считал, что нет ничего в науке вреднее авторитетов.
Да, прав академик
"…Наука оказалась заложником полуфеодальной системы принятия решений и полной безответственности высших должностных лиц. В таких условиях на всех этажах чиновничьей пирамиды нас подстерегают три опасности – невежество, стяжательство и вредительство."
Но это в полной мере относится и к Академии наук, к ее институтам и академикам. У них должно быть коллективное понимание важности той особой роли, которую играет Академия наук и ее институты в научном сообществе. Нужно осознание академиками – членами мозгового центра главного научного центра России своей персональной ответственности за недостатки в науке перед зависимыми от них научными работниками среднего и нижнего уровней, пользующихся в своей творческой деятельности результатами их труда.
Этих специалистов не устраивает часто слишком сложная релятивистская наука с не совсем, а иногда с совсем непонятными им не нужными конструкциями. Это не значит, что это никому не надо. Надо, раз государство за это платит деньги. Но не надо забывать, что академики работают не в простых институтах, а в академических, которым по штату положено заботиться о методологии для научных работников среднего и нижнего уровня. Им нужна более прагматичная наука с понятными "азами", основанными на закономерностях природы. А кому, как не академическим институтам положено это делать?
К сожалению, академические институты наловчились одурачивать депутатов и Правительство, и вместо того, что им НУЖНО делать в соответствии с их статусом, в своих положениях записывают, лишь то, что они МОГУТ делать. Если в такой институт обращается кто-то из нижних инстанций, то применяется стандартная отписка типа «в ответ на Ваше обращение сообщаем, что институт не занимается проблемами, которые Вы поднимаете. Рекомендуем обратиться в другие профильные организации.»
Академик сетует, что Президент «отгородился от народа и даже от парламента». А сами академики не имеют этого недостатка? Имеют. Автор как-то задал вопрос всем математиками, в частности, всем членам Ученого Совета института математики РАН, членам которого является академик Кашин Б.С.: «У Вас все в порядке с основами?» И что? А ничего. Ни один из двадцати членов совета не ответил заявителю. Характерно, что в этом Ученом совете есть и доктора наук, и кандидаты. Тоже, видимо, мания величия заела. Глухое молчание. Как будто нет никакой проблемы. А проблема есть. И большая.
Наведите сначала у себя порядок с основами математики, господа академики. Дайте Путину доступную математическую модель идеального управления, тогда и покритиковать его можно. А то получается, как в басне: «Чем кумушек считать трудиться…» и далее по тексту.
Вопросы математикам, на которые они не знают ответов.
Аспирант:
– Профессор! Скажите, в каких случаях какой
следует применять математический аппарат?
Профессор
(после длительной паузы):
– Молодой человек! Вы слишком
многого хотите от науки!
Аспирант:
– Совсем немного. Хочу, чтобы применяемый
метод исследования объекта определял
соответствующий математический аппарат.
Профессор:
– Увы… пока это невозможно.
(Спустя десятилетия любопытный
аспирант сам решил эту проблему.)
Что такое математика и с чего она начинается? Особую остроту этому вопросу придал выдающийся математик Герман Вейль, сказав, что вопрос об основаниях математики и о том, что представляет собой в конечном счете математика, остается открытым. Современные математики и философы также считают, что кризис математики не преодолен, существует неуверенность в выборе правильного подхода к математике, возникают конфликты по основаниям математики, развитие и применение математической методологии оставляет желать лучшего. Это наверняка известно математикам. Но об этом приходится напоминать, поскольку с точки зрения теории систем возникает ряд тривиальных вопросов к основам математики.
Вопрос № 1:
Все ли математики знают истинное место математики в классификации основных наук?
Вряд ли. Дело в том, что классификация основных наук начинается с системологии, которая является всеобщей (универсальной) методологией всех наук. Она состоит из 4 общих методов: системного подхода, системного анализа, системного синтеза и системотехники. Системотехника здесь содержит слово «техника», имеющее первоначальный древнегреческий смысл «εχνικός», как мастерство или умение применять системные методы в сознательной деятельности.
В каждом из этих методов используется система основные науки: естествознание, философия, математика и техника, как разновидности сознательной деятельности. Причем, каждый метод использует свой присущий только ему раздел науки. Системный подход оперирует материалистической философией и теорией множеств. Системный анализ использует диалектику и комплексный анализ. В системном синтезе философской основой является логика, а математической – векторы. Системотехника применяет философские законы и тензорное исчисление.
Система, как известно, состоит из четырех элементов, расположенных в строгом порядке, где каждый последующий элемент содержит все предыдущие. Поскольку элемент «техника» в данной книге не рассматривается, то «математика» однозначно содержит «естествознание» и «философию».
Именно поэтому математика в своей основе имеет дело с реальными, а точнее, с природными целостными объектами, отображаемыми философскими понятиями и определениями, которые математика моделирует своими условными символами. С этими символами она и работает, создавая модели, реализуемые в будущих реальных объектах. Это прописные истины, над которыми математики, как правило, не задумываются. Они работают с веками созданной математикой и думают, что это так и должно быть. Однако задуматься бы надо. За многие годы известные математики напридумывали много такого, чего в природе не существует, следовательно, не имеет практического применения.
Вопрос № 2:
Известно ли математикам, что любая система, в том числе математическая, имеет всеобщие признаки?
Система первичных математических объектов, как и любая другая, имеет четыре признака:
Количественный – система имеет только четыре структурных образования от одного до четырех взаимосвязанных элементов в каждом;
Метрологический – каждый элемент системы имеет свою меру: реальную величину, изменяющуюся в идеальных пределах;
Качественный – в системе всегда имеется три вида структурных образования по три элемента в каждом: каждый последующий элемент содержит все предыдущие, каждая связь имеет положительное, нейтральное и отрицательное состояния, каждый предыдущий элемент содержит последующий;
Видовой – каждая система имеет четыре вида регулирования (управления): неопределенный – по одному критерию, неоднозначный – по двум критериям, определенный – по трем критериям, однозначный – по четырем критериям.
Вопрос № 3.
Знают ли математики, что их наука содержит систему противоречий?
Очевидно, знают, что есть некоторые противоречия, но какова их система, они вряд ли знают. А она основана на философском понятии «мера». Это единицы измерения, пределы изменчивости, границы перехода из одного состояния в другое (узловые соотношения меры) и отображения (философские отрицания).
Вопрос № 4:
Понимают ли математики, что первичные математические объекты не систематизированы?
У них нет особых претензий к ним: работают с тем, что имеет современная математика. Но при ближайшем рассмотрении претензии возникают к их физической сущности, признакам и определениям. Привязка математических объектов к реальным простейшим элементам Природы выявляет некоторые системные несоответствия. Требуется уточнение их физической природы, функций, структуры и степени определенности.
И здесь возникает целая серия вопросов.
Не совсем понятно, а точнее, совсем непонятно, какими общепринятыми и новыми условными обозначениями, и математическими названиями все это отобразить? В частности, бесконечные множества этих единичных элементов и переходы от одного к другому. Как образуются в энергетической среде космические вихри, которые создают ядра галактик? Как на этих ядрах возникают космические волны, которые превращаются в атомы? Как излучения атомов создают биологические вещества?
Признаки первичных математических объектов.
Даже беглого взгляда достаточно, чтобы понять, что совокупность первичных математических объектов не является системой. Почему это не система и что необходимо сделать, чтобы они стали таковой? В математической справочной литературе и в интернете с некоторой натяжкой можно найти четыре приведенных выше основных первичных структурных образования, но нигде не сказано определенно, сколько подчиненных элементов они должны иметь.
В соответствии с требованиями системности первый элемент (множество) должен быть целостным с единой структурой, второй (функции) должен иметь два элемента, третий (вектор) – три, а четвертый (тензор) – четыре.
1. Количественный признак. Из всех первичных математических объектов только множество соответствует системным требованиям, да и то в качестве неопределенности. Множество является не таким уж простым понятием, как это представляется. Это целая система понятий с разной степенью определенности от абсолютной неопределенности до однозначности.
Множество должно быть количеством чего-то, в данном случае, первичных объектов. как основополагающих: множества, комплексов, векторов и тензоров. Все четыре объекта, как единичные элементы, являются целостными образованиями и образуют соответствующие множества. Схематично это можно представить следующим образом (рис. 1):
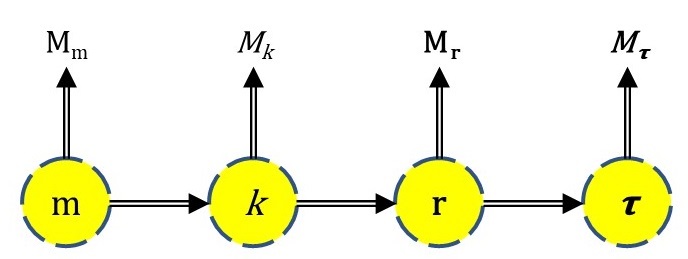
Mm – множество; Mk – множество комплексов; Mr – множество векторов; M𝛕 – множество тензоров.
Рисунок 1. Система множеств первичных математических объектов.
Последовательность внутренних множеств в первичных математических объектах представлена на рис. 2.
Рисунок 2. Последовательность внутренних множеств в первичных математических объектах.
Количественная интерпретация первичных математических объектов, которая отражает их свойство каждого последующего элемента содержать предыдущий, представлена на рис. 3.
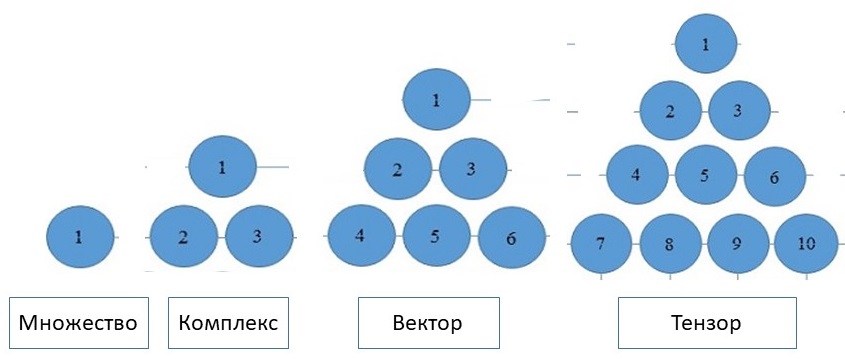
Рисунок 3. Количественная интерпретация первичных математических объектов.
2. Метрологический признак. Единичные элементы этих множеств являются их единицами измерения и представляют собой единственную меру количества. Это, так называемые, одномерные множества.
Все первичные объекты обладают одновременным вращением и перемещением, поэтому одно и тоже множество имеет, с одной стороны, пространство, занятое плотными вращающимися элементами, а, с другой стороны, разреженное пространство, как область их существования при вечном движении. Это двумерное множество или комплексное множество.
Один и тот же элемент в зависимости от его величины и скорости движения может обладать в разное время тремя фазовыми состояниями, подобными состояниям воды. Но все множество разных по величине объектов одновременно имеет три состояния, как например, состояния всех химических элементов на Земле. Это трехмерные множества или векторные множества.
Одни и те же объекты могут находиться в четырех состояниях. Например, из древесины дуба можно изготовить предмет культурного назначения, а можно его химически переработать на дубовый экстракт или использовать на механические цели, а можно просто сжечь как топливо. Это четырехмерные множества или тензорные множества.
Схематично это можно представить следующим образом (рис. 4):
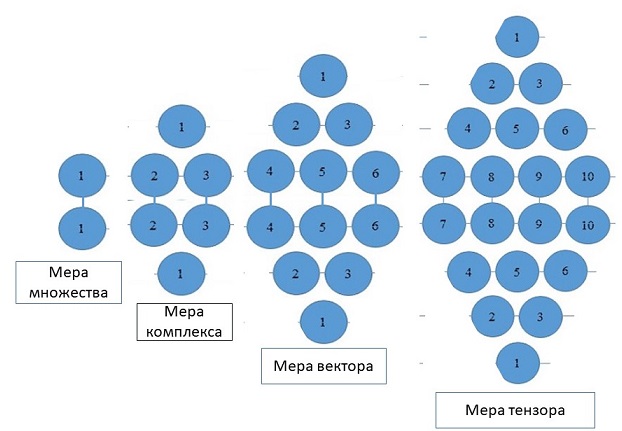
Рисунок 4. Многомерность первичных математических объектов.
3. Качественный признак. Философская категория «качество» отображает структурные элементы системы, но не как взаимодействие всех со всеми, а в строго определенном порядке, когда последующий элемент содержит предыдущий, а значит все предыдущие. Простейший пример представлен на рис. 5.
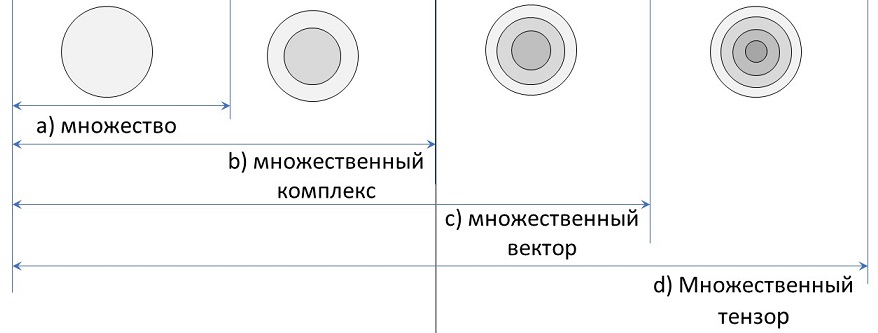
Рисунок 5. Простейший пример взаимодействия
первичных математических объектов
4. Видовой признак. Виды регулирования (управления) характерны для систем разных уровней. Общая схема представлена на рис. 6.
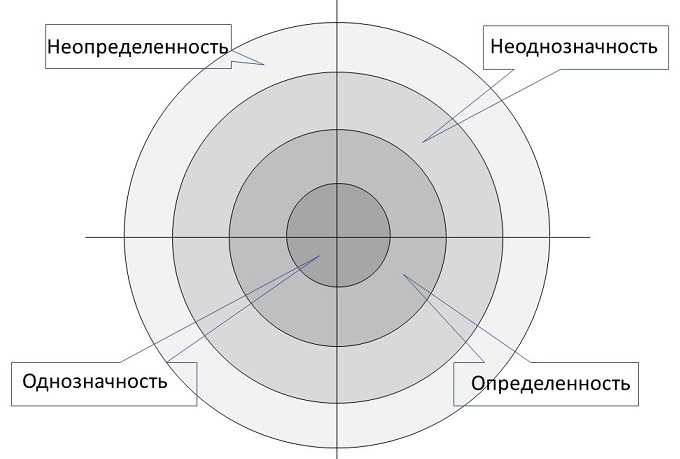
Рисунок 6. Общая схема видовых признаков систем.
Неопределенный вид характерен для бесконечных множеств, представляющих первичную среду существования. Это множество можно назвать бесконечным, а её область существования бесконечностью. Из этой среды образуется ядро космической системы, которое содержит бесконечно большое количество материальных элементов. Их во много раз меньше, чем в среде, но тем не менее их бесконечно большое количество. Если в материальной среде элементом является бесконечно малая единица, то космическим элементом является бесконечно большая единица. В космосе таких единиц бесконечно большое количество.
Таким образом, на космическом уровне существует две единицы и два разных по величине бесконечно больших множества, связанных между собой через единицы. Бесконечно большая единица отличается от бесконечно малой тем, что, помимо вращательного и поступательного движения, свойственного материальным частицам, космический объект, вращаясь, увлекает за собой такое же количество элементов среды, какое содержит сам объект, т.е. имеет внутреннее содержание и внешнюю среду
Именно во внешней среде космического объекта за счет движения единичных элементов материальной среды образуется два вида космических волн. Поперечные волны являются источником создания планет вокруг ядра, а продольные волны создают на планетах материальные оболочки. Размеры начальной амплитуды этих волн соизмеримы с размерами излучаемого объекта. Спирально уменьшающиеся продольные волны, перемещаясь на бесконечно большие расстояния, превращаются в бесконечно малые волновые объекты, из которых образуются элементы атомов. Бесконечно малых атомов имеется бесконечно большое число.
Это третья связанная пара единичных элементов и их бесконечно больших множеств. Причем третий единичный элемент включает в себя свойства движения материальных частиц и внешнюю и внутреннюю структуру космических объектов с их способностью излучать волны. Но атомарные волны в бесконечно большое количество раз меньше космических. Атомарная среда является источником образования третьей совокупности бесконечностей и не может существовать без первых двух.
Атомарные волны, перемещаясь на бесконечные для них расстояния, превращаются в бесконечно малые атомарные волновые объекты, из которых образуются единичные биологические объекты в бесконечно большом количестве. Это четвертая среда, единичный элемент которой, обладая свойствами трех предыдущих, может пребывать в четырех отображенных состояниях, что делает четвертый элемент четырехмерным и с конкретным именем. На этом уровне энергетический запас иссякает и объект «растворяется» в энергетической среде, превращаясь в материальные частицы и замыкая самый большой цикл в природе.
Таким образом, в природе существует четыре иерархических уровня сред, представляющих пары бесконечно больших и бесконечно малых величин (рис.7).

Рисунок 7. Система сред существования.
Следовательно, бесконечности могут четырежды отображаться в другие бесконечности. Это уровни бесконечных величин отображают последовательность физических сред существования: энергетическая, космическая, материальная и биологическая.
Неоднозначный вид характерен для множеств, изменяющихся от единицы до некоторого предела, но обладающих устойчивым равновесием в половине предельного значения.
Первичное множество является верхним уровнем иерархической структуры, который не имеет надмножеств. Но мало кто обращает внимание на то, что у этого множества единичный элемент является наименьшим для данного уровня элементом, не имеющим подчиненных объектов. У первичного бесконечного множества, которое отображает бесконечно большую всеобщую среду существования Природы, элементом является бесконечно малая величина.
А это вместе с бесконечно большим их количеством абсолютно неопределенная основа основ всей математики, обеспечиваемая преемственность всех ее понятий. Это, как раз то, о чем идет речь, как о неопределенном бесконечно большом количестве бесконечно малых объектов в Природе. Трудно представить, какая это малость этот первичный бесконечно малый материальный объект. Но он реален. Не только в материальной среде существует такая первичная пара неопределенных бесконечных величин. В природе существует целая система таких бесконечных множеств.
Числовая ось – количество, а ось координат – мера. Природа устроена таким образом, что все имеет свою меру. Первичная бесконечная материальная среда, существуя в пустоте, имеет свою меру, которой служит пространство. Оно в данном случае, рассматривается как равномерная среда и считается идеализированной осью координат. Количество элементов среды отображается числовой осью.
Вместе они образуют функциональную зависимость, как частный случай множественного комплекса. Два взаимосвязанных множества, которые являются этим целостным образованием, следует назвать комплексными множествами. Для множества реальных элементов служит числовая ось, а для множества их отображения применяется координатная (цифровая) ось как мера количества. Координатной ось в обыденном понимании – это шкала измерений. Числовые оси начинаются с нуля и заканчиваются бесконечно большим числом единиц. Числовой нуль – это число, которого нет, но с него начинаются все числа, образующие числовое множество.
Число либо есть, либо его нет. Это очень важное противоречие, на котором построена целая наука. Координатные же оси такого противоречия не имеют. Они предназначены для выражения цифрами на шкале измерений единиц измерения количества объектов. Здесь нуль и бесконечность числами не являются. Это всего лишь цифры между началом и концом меры чисел на координатной оси.
Особое понимание имеют бесконечно большие и бесконечно малые числа, характеризующие объекты и их количества. Бесконечно большими числами выражаются среды существования, а бесконечно малыми объектами –единичные элементы этой среды.
Вот тут и проявляется ярко выраженное несоответствие идеальных и реальных объектов, которое игнорирует различие между понятием «бесконечность» и «бесконечно большое число». Нельзя сказать, что никто не обращал на то внимания. Например, Г. Кантор применял понятия «оконеченной» или актуальной бесконечности. Но многие великие математики прошлого выступали категорически против этих понятий.
Поэтому и произошла фальсификация этого ключевого момента формирования математики. В частности, математики считают нуль числом и только, но это не совсем так. Функция, выражаемая числами, в осях координат никогда не может превратиться в бесконечность. Она может приобретать бесконечно большие или бесконечно малые, но конечные величины. Этим объясняется отсутствие в природе реального явления, которому соответствует понятие «сингулярность», как понятие – паразит.
Определенный вид характерен для множеств с вполне определенным количеством элементов. Это сфера обыденной деятельности человека в ситуации, когда используется в основном арифметический механизм. Этот вид особых комментариев не требует.







