
Сергей Израйлевич
Опционы: Разработка, оптимизация и тестирование торговых стратегий
1.4. Маркет-нейтральные стратегии
1.4.1. Основные элементы маркет-нейтральной стратегии
Разработка торговых стратегий на основе рационального подхода начинается с определения общей структуры стратегии и ее основных параметров. Это делается как на базе научного подхода (используя знания и предположения, вытекающие из известных или установленных разработчиком закономерностей), так и на основе эмпирического подхода (методами подбора и оптимизации). Во многих случаях целесообразно вначале использовать научный подход для определения интервала допустимых значений того или иного параметра, а затем применять эмпирический подход для нахождения оптимального значения параметра в пределах заданного диапазона. Аналогично научный подход может быть использован для определения исходного множества определенных элементов (например, базовых активов, типов опционных комбинаций, критериев и т. п.), а эмпирические методы могут быть задействованы для выбора оптимального набора элементов в пределах данного исходного множества.
Ниже мы рассмотрим основные структурные элементы маркет-нейтральной опционной стратегии и укажем, какие из них желательно задавать научными методами, а какие – эмпирическими.
Типы опционных комбинаций. Разработчик должен решить, какие типы опционных комбинаций соответствуют разрабатываемой им торговой стратегии. Существует множество стандартных комбинаций, свойства которых хорошо изучены и описаны в литературе. К ним относятся стрэнглы, стрэддлы, различные спреды, кондоры, баттерфляи и многие другие. Кроме того, разработчик может самостоятельно создавать самые разнообразные вариации этих стандартных комбинаций. Решение об использовании тех или иных комбинаций зависит от профиля их платежной функции и от его соответствия логике разрабатываемой торговой стратегии. В большинстве случаев типы используемых комбинаций выбираются научным методом.
Длинные и короткие позиции. Необходимо определить, допустимо ли использование коротких позиций, и, если они допустимы, существуют ли ограничения и требования к соотношению длинных и коротких позиций. Решение этой задачи определяется не только логикой создаваемой стратегии, но зависит также от соображений риск-менеджмента (поскольку короткие позиции по опционам имеют ограниченный потенциал прибыльности и практически неограниченный потенциал убыточности). Кроме того, устанавливая соотношение длинных и коротких позиций, разработчик должен учитывать принятую им систему распределения капитала (поскольку длинные опционы просто покупаются по рыночной цене, а открытие коротких позиций требует депонирования маржи, расчет которой зависит от многих факторов). Обычно вначале устанавливается диапазон допустимых соотношений длинных и коротких позиций (используя научный метод), после чего оптимизируется точное значение (эмпирический метод).
Критерии. Не будет преувеличением сказать, что выбор критериев для оценки, анализа и выбора опционных комбинаций является одним из важнейших решений при создании автоматизированной торговой системы. В первую очередь необходимо определиться, будет ли выбор комбинаций основываться на одном или на многих критериях. В случае если используется несколько критериев, следует выбрать метод многокритериального анализа (методы многокритериального анализа и особенности их практического применения были подробно рассмотрены нами в книге «Опционы: системный подход к инвестициям» и в статьях «Options and the Pareto set» и «Multi-criteria analysis: a practical approach», опубликованных в журнале Futures за 2010 г.). Выбор самих критериев зависит от их свойств и эффективности в решении определенных специфических задач. Определенный критерий может демонстрировать высокую эффективность в одной стратегии, но оказаться непригодным для другой. Важно отметить, что выбор критериев относится к задачам, решаемым методами научного подхода, однако выбор их параметров и оптимизация относятся уже к эмпирической области.
Пороговые значения критериев. Для практического применения критериев необходимо определить их пороговые значения, превышение которых означает пригодность объектов оценки (опционных комбинаций) для данной стратегии. (Если используется Паретовский метод многокритериального анализа, то выбор пороговых значений не требуется.) В принципе, пороговые значения могут выбираться методами оптимизации. Однако, как мы покажем далее, этот параметр может оказывать большое влияние на другие параметры, определяемые не эмпирическими, а научными методами.
Даты экспирации. Общеизвестно, что опционы, относящиеся к разным временным сериям, обладают разными свойствами. Это касается не только скорости временного распада, но и чувствительности к изменениям цены базового актива (дельта), волатильности (вега) и многого другого. Кроме того, спред между ценой покупки и продажи обычно больше для более далеких серий, что приводит к большим проскальзываниям при исполнении. Ликвидность далеких серий также обычно ниже. Помимо всех перечисленных факторов, выбор временных серий влияет на свойства торговой стратегии еще и самым непосредственным образом, поскольку определяет максимально возможный период удержания позиций. Как и для соотношения длинных и коротких позиций, следует вначале установить диапазон допустимых значений, а затем применить оптимизацию.
Диапазон страйков. Этот параметр удобно задавать в виде процента от текущей цены базового актива. Например, диапазон 30 % означает, что торговая стратегия может оперировать только теми опционами, страйки которых находятся в пределах от 70 % до 130 % от цены базового актива. Чем больше значение этого параметра, тем больше комбинаций можно построить для каждого базового актива и тем шире может быть расстояние между страйками в пределах каждой комбинации. Кроме того, необходимо учитывать, что использование более далеких страйков имеет тот же эффект на спреды и ликвидность, что и более далекие даты истечения. Значение диапазона, используемого в торговой системе, чаще всего определяется эмпирическим методом (хотя может применяться и научный подход).
Дельта. В принципе, дельта относится к инструментам риск-менеджмента. Однако для создания дельта-нейтральных позиций необходимо использовать этот показатель уже на начальном этапе формирования портфеля. Дельты опционов, относящихся к разным базовым активам, не обладают свойством аддитивности. Поэтому для портфеля, состоящего из опционов на разные базовые активы, невозможно рассчитать дельту портфеля методом простого суммирования дельт. В этом случае необходимо использовать индексную дельту. Этот показатель выражает меру чувствительности стоимости портфеля к небольшим колебаниям рыночного индекса. Другими словами, он позволяет определить, насколько упадет (или вырастет) стоимость портфеля, если значение индекса изменится на один пункт (или на 1 %). Концепция индексной дельты будет подробно описана в главе посвященной управлению рисками.
После того как все параметры определены и зафиксированы, для того чтобы стратегия приобрела законченный вид, необходимо установить систему распределения капитала между элементами портфеля, определить систему управления общим капиталом (какая доля от суммарного капитала инвестируется в портфель в каждый момент времени), а также разработать систему оценки и управления рисками.
1.4.2. Базовая маркет-нейтральная стратегия
В этом разделе мы опишем наиболее простую форму маркет-нейтральной стратегии. Это будет полезно для дальнейшего более подробного изучения ее основных свойств, структурных элементов и параметров. Кроме того, такую базовую форму маркет-нейтральной стратегии будет удобно сравнивать с другими классами опционных торговых стратегий.
Сигналы на открытие позиций. Предположим, что сигналы на открытии торговых позиций генерируются по показателю единственного индикатора. В качестве индикатора будем использовать критерий «Математическое ожидание прибыли на основе логнормального распределения». Сигналом для открытия позиции является значение критерия, превышающее определенную пороговую величину. В качестве диапазона допустимых значений порогового параметра примем все значения математического ожидания, находящиеся в интервале от нуля до бесконечности. Точное значение порога будет определяться путем оптимизации. Открывающие сигналы генерируются ежедневно и рассчитываются по котировкам закрытия предыдущего торгового дня. Позиции открываются по всем комбинациям, для которых получен сигнал (в объеме свободного, не инвестированного капитала). Для целей моделирования и бэктестинга цена открытия позиции рассчитываются по котировкам закрытия текущего дня.
Сигналы на закрытие позиций. Для базового варианта маркет-нейтральной стратегии будем считать, что все открытые позиции удерживаются до момента истечения опционов. После экспирации все позиции по базовым активам, возникшие в результате исполнения опционов, истекших «в деньгах», закрываются на следующий торговый день.
Индикаторы, используемые для генерирования сигналов. Алгоритм расчета критерия «Математическое ожидание прибыли на основе логнормального распределения» описан в нашей книге «Опционы: системный подход к инвестициям». Для вычисления значений этого критерия необходимо ввести два параметра – математическое ожидание, цены базового актива и дисперсия нормального распределения логарифма цены акции. Значение первого параметра обычно задается изначально разработчиком стратегии исходя из принципов научного подхода. Применительно к маркет-нейтральной стратегии будет естественным принять его равным текущей стоимости базового актива на дату вычисления критерия. Это означает, что текущая цена рассматривается как наиболее вероятная на будущую дату, для которой рассчитывается значение критерия. (Альтернативный подход состоит в придании данному параметру некоего значения, определяемого экспертным путем либо методами фундаментального анализа.) Значение второго параметра можно принять равным квадрату исторической волатильности базового актива. Данный параметр включает в себя дополнительный подпараметр, глубину исторического периода, используемого для расчета исторической волатильности. В большинстве случаев горизонт истории определяется эмпирически путем оптимизации (мы примем его равным 120 дням).
Набор инвестиционных активов. В качестве исходного множества активов, потенциально доступных для торговли, примем все опционы на акции, входящие в состав индекса S&P 500. Объектом инвестирования будем считать не отдельные опционы, а комбинации опционов, относящихся к определенному базовому активу. В качестве допустимого исходного множества для типа опционных комбинаций примем длинные и короткие стрэнглы и стрэддлы. Далее будет показано, что доля различных типов комбинаций в портфеле будет зависеть от многих параметров стратегии.
Требования и ограничения. По соображениям ликвидности и потенциальным рискам проскальзывания допустимо использование только тех страйков, которые расположены не далее 50 % от текущей цены базового актива (то есть если текущая цена акции $50, то могут использоваться только страйки, находящиеся в диапазоне от $25 до $75). По тем же соображениям недопустимо использование временных серий, отстоящих более 200 дней от даты истечения. Указанные диапазоны, ограничивающие область допустимых значений, определены исходя из априорных предпосылок (использован научный подход). Точные значения параметров будут определяться путем оптимизации.
Принципы управления капиталом. Применительно к данной стратегии решение задачи управления капиталом сводится к распределению средств между безрисковыми инструментами денежного рынка и инвестиционным портфелем. В каждый момент времени необходимо определять, какая часть свободного капитала инвестируется в позиции, по которым получены открывающие сигналы. Для базового варианта маркет-нейтральной стратегии примем наиболее простой принцип, когда доля инвестируемого капитала всегда составляет 100 % (то есть весь капитал участвует в игре и все средства, высвобождающиеся в результате закрытия позиций, немедленно реинвестируются).
Распределение капитала между элементами портфеля. Распределение капитала между комбинациями, вошедшими в состав портфеля, будет осуществляться по принципу эквивалентности позиции в акциях. В соответствии с этим принципом размер позиции по каждой комбинации выбирается таким образом, что в случае исполнения опционов сумма вложений во все базовые активы будет приблизительно равной (более подробно этот принцип будет рассмотрен далее). Если в определенный момент времени имеется С свободных средств и получено m сигналов на открытие позиций, то объем позиции по каждой комбинации определяется следующим образом:

где Sc и Sp – страйки опционов колл и пут, Np и Nc – количество покупаемых или продаваемых опционов пут и колл соответственно. Применение данной формулы требует принятия допущения о бесконечной дробимости опционных контрактов. Хотя это допущение нереалистично (поскольку большинство опционных контрактов включают по 100 опционов), оно не повлияет на результаты наших исследований.
Методы и инструменты управления рисками. Как следует из природы дельта-нейтральной стратегии, основным ориентиром при управлении рисками данной стратегии является соблюдение принципа дельта-нейтральности портфеля. Соответственно, основным инструментом управления рисками является индексная дельта. Устанавливая значения различных параметров стратегии, необходимо стремиться к тому, чтобы индексная дельта портфеля равнялась нулю или находилась в близком к нулю и узком диапазоне допустимых значений этого показателя. Другие показатели риска, включающие в себя VaR, коэффициент асимметричности и вероятность убытка, могут использоваться в качестве вспомогательных инструментов управления рисками (эти показатели будут подробно описаны в главе, посвященной управлению рисками).
1.4.3. Построение точек и границ дельта-нейтральности
В двух предыдущих разделах были описаны основные компоненты дельта-нейтральных стратегий. Нетрудно заметить, что даже наиболее простой базовый вариант стратегии содержит довольно большое количество параметров, для которых необходимо установить и зафиксировать определенные значения. Наличие даже нескольких параметров означает, что существует большое количество различных вариантов комбинирования их значений (увеличение идет по степенному закону). Следует отметить, что для большинства сочетаний значений параметров дельта-нейтральность недостижима.
Для базового варианта дельта-нейтральной стратегии можно выделить три основных параметра, которые непосредственно влияют на состав и структуру портфеля. К ним относятся:
• пороговое значение критерия, используемое для генериро- вания сигналов на открытие позиций;
• диапазон страйков, разрешенных для использования при построении комбинаций;
• разрешенные временные серии опционов (определяющие период времени, остающийся до даты экспирации).
Фиксируя значения этих параметров, разработчик торговой стратегии должен принимать во внимание их влияние на такие важные характеристики портфеля, как соотношение длинных и коротких позиций, соотношение различных типов опционных комбинаций, диверсификацию портфеля и характеристики риска. Однако в первую очередь необходимо определить зависимость индексной дельты портфеля от величины каждого из трех параметров (и от их различных сочетаний). Ведь если для большинства допустимых значений параметров индексная дельта портфеля существенно отклоняется от нуля, то построение дельта-нейтральной стратегии в принципе недостижимо.
Каждую комбинацию значений параметров, для которой соблюдается условие дельта-нейтральности (дельта портфеля равна нулю), мы будем называть точкой дельта нейтральности. А всю совокупность таких точек будем называть границей дельта нейтральности.
Для начала рассмотрим на нескольких примерах процедуру нахождения точек дельта-нейтральности. Предположим, что с целью получения торговых сигналов мы оцениваем исходное множество комбинаций, построенных для всех акций индекса S&P500. Оценка производится по критерию «математическое ожидание прибыли на основе логнормального распределения» (в соответствии с процедурой, описанной выше, для базовой стратегии). Допустим, что параметр «диапазон страйков» зафиксирован на значении 10 % от цены базового актива. Для параметра «время до экспирации» исследуем несколько значений: одна неделя, один, два и три месяца до экспирации. Для определения точек дельта-нейтральности 11 января 2010 г. были сгенерированы торговые сигналы для следующих дат экспирации: 15 января 2010 г. (одна неделя до экспирации), 19 февраля 2010 г. (один месяц до экспирации), 19 марта 2010 г. (два месяца до экспирации), 16 апреля 2010 г. (три месяца до экспирации).
Определим точки дельта-нейтральности для всего диапазона значений параметра «порог критерия». Для этого необходимо рассмотреть зависимость индексной дельты портфеля от величины порога. На рис. 1.4.1 представлены такие зависимости для четырех дат экспирации (в этом примере использовались страйки, лежащие в диапазоне 10 % от цен базовых активов). Дельта-нейтральными являются точки, лежащие на пересечении линии графика с горизонтальной осью. Соответственно, каждая точка пересечения горизонтальной оси указывает на величину порога, для которой соблюдается условие дельта-нейтральности. (Порог критерия равен координате на горизонтальной оси.)
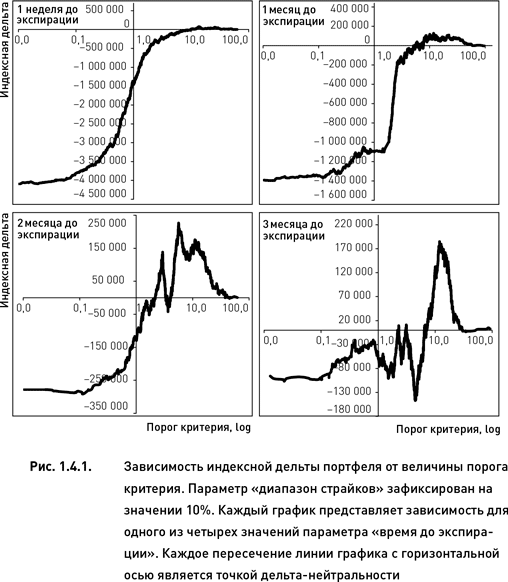
Для четырех частных случаев, представленных на рис. 1.4.1, дельта-нейтральность достигается при величине порога от 2 % до 10 % (значения критерия и порога выражаются как математическое ожидание прибыли в процентах от объема инвестиций). Так, для случая, когда до экспирации остается одна неделя, существует всего одна точка дельта-нейтральности, приходящаяся на порог 9 %. Это означает, что если для данной временной серии построить комбинации, используя опционы, страйки которых лежат в диапазоне (цена базового актива ±10 %), и отобрать те из них, для которых значение критерия > 9 %, то мы получим дельта-нейтральный портфель.
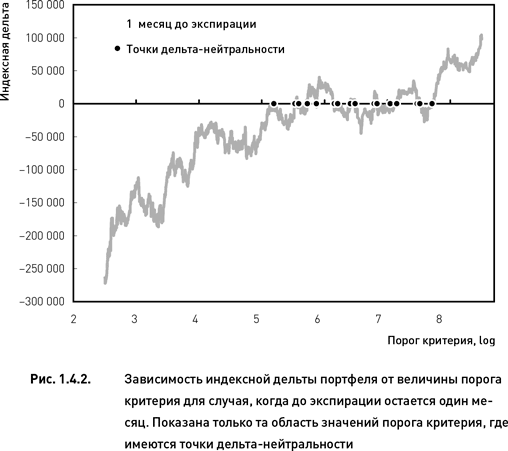
В том случае, когда до экспирации остается месяц, существует множество точек дельта-нейтральности (поскольку линия дельты пересекает график в нескольких местах). Пересечения происходят в достаточно узком диапазоне значений порога, создавая своего рода отрезок дельта-нейтральности. На рис. 1.4.2 показан этот отрезок в более крупном масштабе, что позволяет рассмотреть каждую точку дельта-нейтральности по отдельности. Всего таких точек насчитывается 16, и они располагаются в интервале от 5 до 8 %. (Другими словами, значения порога критерия, для которых соблюдается условие дельта-нейтральности, находятся в интервале 5–8 %.) В том случае, когда значение параметра «время до экспирации» было принято равным двум месяцам, были обнаружены три точки дельта-нейтральности, а для трех месяцев – пять точек.
Заслуживает внимания тот факт, что для одной недели до экспирации линия индексной дельты является относительно гладкой и имеет форму классической логической кривой (верхний левый график на рис. 1.4.1). Для двух месяцев эта линия становится более ломанной, однако все еще сохраняет более-менее правильную форму (верхний правый график на рис. 1.4.1). В тех же случаях, когда портфель формировался из более далеких опционных серий (два и три месяца), линия дельты принимает все более хаотичный вид (нижние графики на рис. 1.4.1). Это означает, что дельта комбинаций, состоящих из опционов с близкой датой экспирации, приблизительно одинакова, если эти комбинации имеют приблизительно равные значения критерия. Если же комбинации строятся из дальних опционов, то их дельты гораздо более изменчивы даже в том случае, когда они оцениваются критерием приблизительно одинаково. Из этого следует, что выбор определенного сочетания значений параметров для построения дельта-нейтральных портфелей будет тем более надежен и устойчив, чем более близкие даты экспирации будут использоваться при создании опционных комбинаций.
Также следует отметить, что по мере роста значений параметра «порог критерия» индексная дельта портфеля, состоящего из опционов с близкой датой экспирации, изменяется в очень широком диапазоне. При этом дельта портфеля, сформированного из дальних опционных серий, находится в гораздо более узком диапазоне (сравни верхний левый и нижний правый графики на рис. 1.4.1). Это объясняется тем, что при прочих равных условиях дельта опционов растет по мере приближения даты экспирации (если опцион находится в деньгах и до истечения остается немного времени, то его дельта приближается к +1 или –1). Для нас из этого следует важный вывод о том, что если при создании портфеля мы несколько отступили от заданной комбинации значений параметров (при которой портфель является дельта-нейтральным), то отклонение от дельта-нейтральности будет гораздо большим при использовании опционов с близкой датой экспирации.
Теперь перейдем к процедуре нахождения границ дельта-нейтральности. Для трех параметров, определенных нами как наиболее существенных, зафиксируем сначала «время до экспирации» и исследуем все возможные сочетания значений двух других параметров – «порог критерия» и «диапазон страйков». Для этого необходимо рассчитать величину индексной дельты для каждого варианта (порог критерия × диапазон страйков) во всем диапазоне их допустимых значений. Затем полученные данные следует представить в виде топографической карты, где горизонтальная и вертикальная оси соответствуют значениям исследуемых параметров, а каждая точка на карте выражает высотную отметку, соответствующую величине дельты. Точки с одинаковыми высотными отметками на такой карте соединяются изолиниями. Изолиния, проходящая по нулевой отметке, является искомой границей дельта-нейтральности.
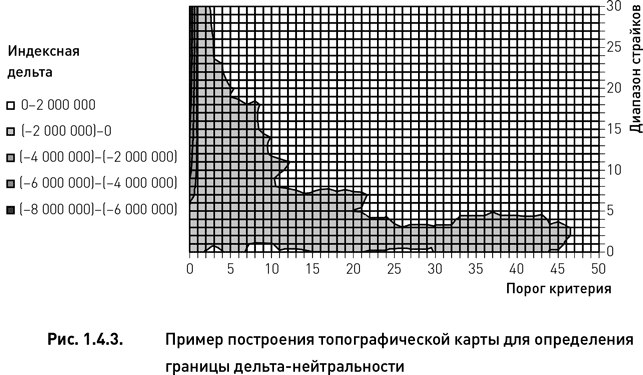
На рис. 1.4.3 представлен пример топографической карты для значения параметра «время до экспирации», равного одной неделе (были использованы те же данные, что и при построении верхнего левого графика на рис. 1.4.1; дата создания портфеля – 11 января 2010 г., дата экспирации – 15 января 2010 г.). Граница дельта-нейтральности проходит по диагонали от верхнего левого угла карты к правому нижнему углу. Справа от границы находятся портфели с положительными значениями индексной дельты, а с левой стороны – портфели с отрицательной дельтой. При очень низких значениях порога критерия (левый край карты) дельта портфелей достигает очень больших отрицательных значений.
Заметьте, что верхний левый график на рис. 1.4.1 в точности соответствует горизонтальной линии на карте, проходящей через диапазон страйков, равный 10 % (рис. 1.4.3). То есть если провести мысленный разрез по данной горизонтали и представить себе боковой вид данного разреза, то мы получим профиль, полностью совпадающий с линией индексной дельты на рис. 1.4.1. Таким образом, совокупность точек дельта-нейтральности, полученных по описанной выше методике, формирует границы дельта-нейтральности.
Глядя на топографическую карту, представленную на рис. 1.4.3, легко определить, что дельта-нейтральный портфель может быть сформирован при достаточно большом количестве сочетаний параметров (порог критерия × диапазон страйков). Например, можно построить портфель, состоящий из комбинаций, для которых значение критерия больше 5 %, а диапазон страйков достаточно широк (цена ± 20 %). С другой стороны, можно предпочесть дельта-нейтральный портфель, включающий комбинации только с большими значениями критерия (например, больше 15 %). Но тогда придется ограничиться довольно узким диапазоном страйков (цена ± 6 %). И так далее.
Описанная методика нахождения границ дельта-нейтральности представлена здесь в виде визуальных процедур. Это сделано исключительно для наглядности и простоты изложения материала. На практике визуализация границ не требуется, они могут быть определены расчетными методом, используя компьютерные алгоритмы. Вместе с тем построение подобных топографических карт может быть полезно для осмысления взаимозависимости параметров и выбора диапазонов их допустимых значений.
Необходимо отметить, что для целей создания автоматизированной торговой системы мы не можем ограничиться использованием карты подобной той, что изображена на рис. 1.4.3, поскольку она представляет собой единичный случай. А автоматизированная системная торговля характеризуется именно тем, что решения принимаются не по результатам изучения единственной карты, а на основе устойчивых закономерностей, установленных на достаточно широком фактическом материале. Кроме того, следует рассмотреть, зависит ли расположение границ дельта-нейтральности от состояния рынка. Логично предположить, что в периоды высокой волатильности границы выглядят иначе, чем во время спокойного рынка. Именно поэтому мы переходим теперь к изучению границ дельта-нейтральности, построенных на более широкой статистической базе, включающей как спокойные, так и экстремальные (кризисные) периоды.


