
Ллойд Арнольд Браун
История географических карт
Вторую зарегистрированную попытку измерить Землю предпринял Посидоний из Апамеи. Его результат был не слишком хорош, но он заслуживает места в нашей истории из-за смятения, которое вызвал среди ранних историков; кроме того, именно его результат, переданный Страбоном, а не результат, полученный Эратосфеном, несколько сотен лет считался общепринятым.
Посидоний (ок. 130—51 гг. до н. э.) был одним из наиболее образованных философов-стоиков. Прозванный Родосцем, он руководил школой на острове Родос, привлекавшей ученых со всех концов света. Хотя, как выразился один историк, Посидоний не был астрономом «в строгом смысле этого слова», его философия тем не менее охватывала не только астрономию, но и географию, математику и метеорологию; кроме того, он написал «Историю» в 52 книгах. В некоторых отношениях он превзошел астрономов – например, измеренное им расстояние от Земли до Солнца оказалось ближе к истине, чем величина, полученная Гиппархом. Его метод измерения Земли основывался на тех же общих принципах, что и метод Эратосфена, но, вместо вычисления разницы в высоте солнца в день летнего солнцестояния в двух разных местах, Посидоний использовал звезду. Клеомед в деталях описал эту историю следующим образом:
«В некоторых частях Греции невозможно увидеть яркую звезду Канопус, но на Родосе, где работал Посидоний, она поднималась достаточно, чтобы скользнуть по горизонту и тут же снова нырнуть обратно. В Александрии, еще южнее, высота Канопуса на меридиане равнялась «четвертой части «знака», то есть одной сорок восьмой части зодиакального круга. Конечно, это просто другой способ сказать, что разница в угловой высоте Канопуса в Александрии и на Родосе составляет 7°30'. Считалось, что линейное расстояние между этими двумя пунктами составляет 500 миль; таким образом, получаем окружность земли 48 х 500, или 24 000 миль».
Опять, использованный Посидонием метод был достаточно разумен, но результат получился ошибочным из-за неточных данных. Во-первых, угловое расстояние между Родосом и Александрией (то есть разница по широте) составляет не 7°30', а 5°15' – меньше одной шестидесятой части большого круга. Хит указывает, что ошибка определения высоты звезды по меридиану имела место, скорее всего, на Родосе, где эффекты рефракции на горизонте должны были серьезно затруднять наблюдения; другими словами, провести точное наблюдение звезды, едва-едва проскальзывающей по горизонту, очень трудно, если не невозможно. Вторая ошибка, расстояние в 500 миль между Александрией и Родосом, возникла в результате того, что оценивали расстояние моряки – люди, никогда не отличавшиеся тягой к преуменьшению. Расстояние оценивали по максимуму. Некоторые специалисты оценивали это расстояние в 400 миль, а Эратосфен, согласно Страбону, сказал, что оно не превышает 375 миль. Однако по оценке Посидония, которую привел Клеомед, окружность Земли все же составляла 24 000 миль. Она бы и осталась таковой, если бы не Страбон. Но, обсуждая последние опыты по измерению Земли, Страбон упоминает «того, который делает окружность Земли самой маленькой… а именно опыт Посидония, который оценивает ее окружность примерно в 180 000 стадиев [18 000 миль]…».
Откуда взялась такая огромная разница между величинами, приведенными Клеомедом и Страбоном? Хит предлагает остроумное объяснение, при котором оба источника оказываются в какой-то мере правы. Страбон, рассуждает он, склонен был верить Эратосфену и критически относился к общепринятому мнению по любому вопросу, не обязательно научному. Поэтому, переходя к расчетам и выводам Посидония, он отвергает общепринятую величину расстояния между Александрией и Родосом в 500 миль и использует вместо этого расстояние, названное Эратосфеном – 375 миль. В то же время оба автора, рассказавшие о Посидонии (и Клеомед, и Страбон), по всей видимости, согласны, что угловое расстояние между двумя пунктами составляет одну сорок восьмую часть меридионального большого круга. Теперь посмотрим: 48 раз по 500 миль составит 24 000 миль, а 48 раз по 375 миль – 18 000 миль. Если мы примем эти рассуждения, то придется сделать вывод, что или Клеомед, или Страбон, или оба автора работали только с изложением рассуждений Посидония, то есть с описанием его метода без числовых значений, и взяли на себя смелость добавить недостающие детали самостоятельно. Однако Страбон – всем историкам историк – привел меньшую из двух величин, и в результате общее признание получила длина земной окружности равная 18 000 миль. Соответственно один градус дуги считался равным 50 милям. Этим двум стандартам суждено было изменить ход истории и долгие годы причинять мучения многим поколениям географов.
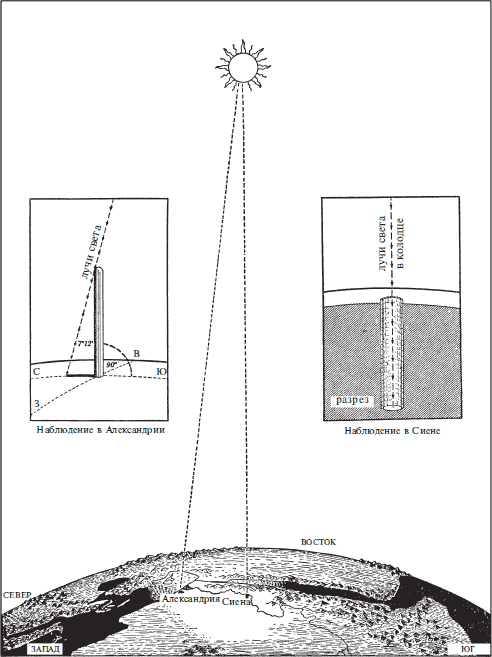
Самое раннее известное измерение окружности Земли провел Эратосфен около 240 г. до н. э. Его вычисления базировались на 1) угловой высоте солнца и 2) линейном расстоянии между Александрией и Сиеной
Обсуждая прогресс картографии, Страбон ссылается на карты, нарисованные «древними», но, следуя провозглашенному им самим принципу – игнорировать всех, кроме самых авторитетных из «современных» авторов, – он не говорит почти ничего, что могло бы указать нам, насколько на самом деле древни эти «древние». Он не называет никого из них по имени и вообще очень неопределенно говорит о развитии картографии до Гомера. Тем не менее изготовление карт – возможно, древнейшая разновидность примитивного искусства, поскольку с самого начала у этого искусства была цель. Это искусство столь же старо, как первые линии, проведенные человеком на песке или на стене пещеры. Более того, способность изобразить кусок земной поверхности – хотя бы небольшой – с помощью палочек и камешков или куска мела настолько универсальна, что, возможно, ее можно даже рассматривать как инстинктивную. Бесчисленные исследователи, имевшие дело с примитивными племенами, отмечали этот факт. Когда все остальные методы общения ничего не дают, на помощь приходит универсальный язык примитивной карты или схемы.
Самые ранние карты базировались на личном опыте и знакомстве с местностью. Они показывали путь через лес до соседнего племени; места, где можно обнаружить дичь, воду или соль; направление и расстояние до вражеских племен. Кочевой образ жизни несколько усложнял картину; бродячим племенам необходимо было знать, как пересечь пустыню и не умереть от жажды и как добраться домой за много миль после летнего выпаса скота. Чтобы начать войну – то есть приобрести землю этим древнейшим способом, – нужно было знать территорию соседей и хорошо в ней ориентироваться. Для торговли с другими племенами и народами нужны были еще большие знания о расстояниях и направлениях; чем дальше располагались рынки, тем точнее должны были быть к ним маршруты. По мере распространения цивилизации знания о расстояниях и направлениях приобретали все большее значение. Подобно записям ранних астрологов, географические описания и рисунки, рассказывающие, как добраться из одного места в другое, наносились – тем или иным способом – на камень, папирус или пергамент. Почти ничего из этих записей не сохранилось.
Карты и глобусы «древних», о которых говорит Страбон, делятся на две большие группы: представления мира в целом и карты небольших участков местности. Какая группа возникла первой – неясно, так как на самых ранних картах изображение родного городка можно с тем же успехом рассматривать как карту мира, ибо человек, нарисовавший карту, изобразил на ней именно это: свой мир – плоскую поверхность, центр которой, или точку наблюдения, можно обозначить как X и пределы которой ограничены кругом горизонта, видимого из этой точки. Круг горизонта и круг мира расширялись в прямой пропорции к росту мобильности человека; он, вероятно, не раз задумывался над тем, как далеко нужно заехать, чтобы добраться до горизонта – места, откуда можно спрыгнуть вниз. Если говорить в масштабах наций, в мире в то время существовало несколько географических центров. Для эллинов центром мира была Греция, а центром Греции – Дельфы. Каждая нация в своем развитии проходила эту стадию, и в какой-то момент у мира было столько же центров, сколько в нем существовало стран. Мир в форме диска – или по крайней мере то, что осталось от этой концепции со времен Гомера, – расширился в конце концов до того, что стал охватывать весь бассейн Средиземного моря, Черное море, Египет, Вавилон и Ассирию, но карт этого мира не существует. Все, что можно доказать на основании литературных источников, – что в дохристианскую эпоху такие карты существовали.
Самые ранние свидетельства изготовления карт исходят из Вавилона, где кадастровая съемка (то есть составление планов земельных владений) в целях налогообложения собственности проводилась еще во времена Саргона Аккадского (ок. 2300 г. до н. э.). В Британском музее имеются глиняные таблички, датируемые 2300–2100 гг. до н. э., с записями по земельной съемке. На одной из таких табличек грубо изображена часть Нижней Вавилонии в окружении «соленой реки», или Океана. Папирус, хранящийся в Туринском музее, изображает триумфальное возвращение Сети I (1366–1333 гг. до н. э.) из Сирии; на нем показана дорога из Пелузия в Героополь, украшенная изящными рисунками. Аполлоний Родосский, ставший библиотекарем Александрии в 196 г. до н. э., писал в своей «Аргонавтике», что обитатели Колхиды – колонии, возникшей во времена Рамсеса II (ок. 1250 г. до н. э.), – передают из поколения в поколение некие резные деревянные таблички, на которых точно изображены Земля, море, дороги и города. Существует и еще несколько образцов ранних карт и планов, изготовленных за тысячу или более лет до Анаксимандра, которого греки почитали как изобретателя картографии.
Даже в самых ранних литературных произведениях, имеющих отношение к картографии, можно обнаружить упоминания о карте мира – не важно, что думали в тот момент о размерах и форме Земли. Гекатей, так бойко писавший о своих путешествиях по всему миру, оставил после себя бронзовую табличку с выгравированной надписью «весь круг Земли, море и реки». Геродот сообщил, что около 500 г. до н. э. эту карту показывал Клеомену, царю Спарты, Аристагор, тиран Мнлета, пытавшийся организовать восстание против персов и нуждавшийся в помощи спартанцев. Эта карта, вероятно, представляла собой переработку более ранней карты, изготовленной Анаксимандром.
В комедии Аристофана «Облака» (423 г. до н. э.) на сцену выносили карту мира, на которой ученик Сократа показывал аудитории знакомые места, например Афины. Звучал следующий диалог:
«С т р е п с и о д. Так, а вот это (указывает на какой-то геометрический инструмент); для чего оно?
У ч е н и к. Чтоб мерить Землю.
С т р е п с и о д. Надельную?
У ч е н и к. Да нет! Всю Землю… А здесь изображенье всей Вселенной. Вот Афины. Видишь?»
Демокрит из Абдеры (ок. 450–360 гг. до н. э.), выдвинувший вместе с Левкиппом атомарную теорию, изготовил карту обитаемой части мира. Дикеарх из Мессены, ученик Аристотеля (326–296 гг. до н. э.), составил описание Земли и проиллюстрировал его картами. По всей вероятности, частью его работы был также трактат о методе измерения высоты гор.
Имеются упоминания о достаточном количестве ранних глобусов, чтобы сделать вывод: глобусы стали довольно широко использоваться вскоре после того, как теория шарообразности Земли получила общее признание. В Музее Неаполя имеется глобус двухметрового диаметра, изготовленный, вне всякого сомнения, в IV в. до н. э. Глобус покоится на плечах человеческой фигуры, изображающей Атланта. Возможно, это создание Евдокса (ум. 386 г. до н. э.) – знаменитого астронома и философа. Арат из Солы (род. 315 г. до н. э.) в своем поэтическом произведении «Прогностика» упоминает имевшийся у него глобус. У Архимеда был стеклянный лунный глобус, внутри которого был подвешен маленький земной глобус. У геометра Герона из Александрии был такой же. Гиппарх, астроном-библиотекарь, тоже пользовался в своей библиотеке глобусом. Примерно в 140 г. до н. э. Кратет из Маллы сделал глобус и отразил на нем концепцию мира, которой придерживались стоики.
Среди «Разных историй», собранных Элианом в III в. н. э., одна иллюстрирует развитие картографии вплоть до Страбона. «Когда Сократ увидел, как Алкивиад надувается от богатства, хвалится его обилием, а еще больше землями, он отвел его в одно место в городе, где помещена была таблица с изображением земного круга, и попросил его найти на ней Аттику. Когда Алкивиад нашел ее, Сократ попросил его показать на табличке принадлежащие ему земли. Когда же тот ответил: «Но они нигде не нарисованы», Сократ сказал: «Ну вот, значит, ты хвалишься ими, а они даже не являются частью Земли»». В 25 г. н. э. мало кто из людей мог подойти к карте и сказать: «Вот моя земля, а вот это моя страна». Мало кто мог назвать страны, лежащие на берегах «нашего моря», а пределы населенного мира в значительной степени оставались загадкой.
Глава II
Обитаемый мир
Если Земля – в самом деле шар, да еще большой (то есть хотя бы приближается по величине к размерам, названным Эратосфеном), то перед философами и астрономами, географами и геометрами вставало несколько интересных вопросов. Какая часть Земли пригодна для жизни и какая ее часть в самом деле обитаема? Безусловно, не вся. Ходили какие-то слухи о далеких странах за Геркулесовыми столпами, а также в отдаленных районах Дальнего Востока. Если эти страны в самом деле существуют, то как далеко находятся они от цивилизованного мира, и как геометрам отделить обитаемую часть мира от той его части, где жизнь невозможна? Короче говоря, как можно разделить, классифицировать и упорядочить сферическую Землю, если опереться при этом практически не на что?
Дикеарх[13] из Мессены начал с того, что провел на карте прямую линию восток—запад через весь известный ему обитаемый мир. Эта «диафрагма» или «разделитель», как его называли, проходил от Геркулесовых столпов через Средиземное море вдоль гор Тавр и Имаус (Гималаи) к Восточному океану. Как прямая разделительная линия восток—запад, диафрагма не особенно удалась. Точное местонахождение ее западного конца даже триста лет спустя вызывало сомнения – по крайней мере, в географических кругах, и Страбон долго рассуждает о том, что когда-нибудь в будущем, возможно, удастся определить положение столпов. Направляясь от столпов к востоку, линия быстро перестает быть прямой; по мере того как Дикеарх называет точки, через которые она должна пройти, линия отклоняется сначала к северу, затем к югу. К востоку от Средиземного моря линия пересекает горы, известные только по слухам, и доходит до океана, о существовании которого можно было только догадываться. Получалось, что разделить земной шар не так уж просто; в поисках отправной точки или линии, а также способа сделать так, чтобы линия всегда шла в нужном направлении, географы вновь обратились к небесам, а именно к Солнцу. Именно Солнце привнесло в картографию три первые разделительные линии, придавшие термину «параллель» определенное значение, – экватор, тропик Рака и тропик Козерога.
Главными фактами о поведении солнца в примитивной цивилизации владел каждый человек – пастух или фермер, рыбак или погонщик верблюдов. Как все живое, человек нуждается в солнечном тепле; мало того, солнечное тепло должно обеспечить ему средства к существованию, заставить расти траву и хлебные злаки. Человек знал, что именно солнце дает и поддерживает жизнь, а потому живо интересовался его привычками задолго до того, как жречество взяло на себя ответственность за ведение календаря и предсказание затмений. Человек начал изучать солнце раньше, чем поклоняться ему. Кое-какие особенности нашего светила очевидны любому наблюдательному человеку – не считая того, что каждое утро оно поднимается в небеса в одной области неба и каждый вечер садится на противоположной стороне. Оно не всегда встает и садится в одном и том же месте. В определенное время года оно поднимается поздно, а садится рано; в другое время – встает рано, а садится поздно. Дуга, которую солнце описывает по небу, меняется день ото дня и от месяца к месяцу. Это важно, так как любое заметное изменение высоты солнца вызывает смену времен года. Меняется не только продолжительность дня и ночи, но и их температура. С этими изменениями связаны и цикл роста растений, и период размножения животных. В тот день, когда солнце стоит ниже всего над горизонтом, когда ночь длиннее всего, а солнце появляется так ненадолго, что не в состоянии согреть тело, – даже в этот день и час, сулящий телу одни лишь страдания, можно утешаться тем, что завтра тепла станет чуть больше, а ночь будет чуть короче, хотя, возможно, такой же холодной. Зимнее солнцестояние (21 декабря) праздновали задолго до рождения младенца Христа. Почему? Потому что после этого дня солнце возвращается в мир. Через три месяца, когда оно пройдет половину пути, а день и ночь сравняются (равноденствие), появится следующий повод для праздника; в это время жизнь бурлит, а все живое активно размножается. Возрождается не только земля, но и сама жизнь. В самый длинный день года, когда солнце поднимается в небесах выше всего и сияет в полном блеске, тоже есть повод для ликования; для многих это время жатвы, для других – просто время, когда в середине дня лучше не выходить из дома. В это время Шамаш действительно становился «губителем» и «сжигателем». И все же летнее солнцестояние (21 июня) олицетворяет все то хорошее, что дарует бог-солнце смертному человеку. Вскоре вновь наступит осеннее равноденствие, и земля вновь начнет умирать.
Чтобы предсказать эти вещи, не нужны жрецы – точно так же, как не обязательно быть астрологом, чтобы сказать, что Полярная звезда год от года остается неподвижной, тогда как миллионы других звезд ходят вокруг нее справа налево. Подобные вещи общеизвестны, хотя необразованный человек и может на день-другой ошибиться в определении момента этих фундаментальных солнечных перемен. Однако ориентация древних монументов, таких как монументы Стонхенджа, указывает, что древний человек использовал все доступные ему средства, чтобы точно отслеживать важные сезонные изменения. Он научился размещать метки таким образом, чтобы грубые средства позволяли отслеживать ежегодное перемещение точки восхода солнца с юга на север вдоль восточного горизонта и определять по нему, когда нужно праздновать и когда горевать. Египетские и халдейские жрецы усовершенствовали методы древнего человека и точно определили дни важных сезонных перемен, а греческие философы при помощи гномона и солнечных часов продвинулись еще на шаг вперед. Они спустили равноденствия и солнцестояния на землю и использовали их для составления карт.

Примитивный человек знал поведение солнца изо дня в день и от года к году. Астрономы отметили дни равноденствий и солнцестояний
Гномон был инструментом поистине низкого происхождения. В самой примитивной форме это пастушеский посох, воткнутый в песок палаточный шест или любой другой стержень, дерево или вертикальная палка; отбрасывая тень, он тем самым указывает на солнце. Направление тени подсказывало пастуху или ростовщику время дня, а ее длина – время года. Для наблюдателя первое более очевидно, чем второе, но именно отношение длины гномона к длине отбрасываемой им тени было впервые применено в картографии и определило три первые широтные линии на карте. Равноденствие – когда день равен ночи – наступает дважды в год. Для обитателей Земли это середина между северным и южным пределами ежегодного солнечного паломничества по небесам. В дни равноденствия солнце встает на востоке и садится на западе; астрономы говорят, что в эти дни в полдень гномон на равноденственной линии не отбрасывает тени, так как солнце находится точно над головой. Равноденственная линия является одновременно и «экваториальной» – воображаемым большим кругом, проведенным под прямым углом к земной оси и разделяющим земной шар на Северное и Южное полушария. Астрономам это было известно давно, но долгое время этот факт никак не отражался на изготовлении карт в целом и на карте обитаемого мира в частности, поскольку район равноденственной, или экваториальной, линии считался непригодным для жизни, а значит, неинтересным для географов. Однако постепенно, с течением времени, географы и картографы позаимствовали у астрономов эту первую и самую понятную базовую линию. Можно назвать несколько неоспоримых ее достоинств. Во-первых, она делит земной шар геометрически очень аккуратно – пополам, перпендикулярно к земной оси, что не может не нравиться математическому сообществу. Во-вторых, ее удобно было использовать как базовую опорную линию, относительно которой можно было теоретически вычислять данные обитаемых районов земли, не покидая при этом пределов цивилизации. В-третьих, эта линия подарила человечеству стандартный день. День равноденствия – средний день в отношении продолжительности светлого времени. Песочные часы и клепсидры (водяные часы) градуировали на основе длины именно этого – равноденственного – дня от восхода до заката; на них отмечали часовые, получасовые и четвертьчасовые промежутки. В этот же день устанавливали и точно ориентировали солнечные часы. Несомненно, существовало немало способов определить день равноденствия – для этого не обязательно было доверяться календарю или использовать вычисления астрономов, которые вряд ли были широко известны. Для любого из практических методов достаточно было иметь под рукой гномон или солнечные часы.


Самая ранняя известная карта (сверху), обнаруженная в Нузи возле Киркука, датируется периодом династии Саргона Аккадского, примерно 2400–2200 гг. до н. э. Вавилонская табличка снизу – план местности, датированный VI или VII в. до н. э.
Вторая и третья параллели, нанесенные на сферическую Землю, тоже были тесно связаны с экваториальной, или равноденственной, линией; кроме того, они были буквально параллельны ей. Страбон и его «древние» называли их, вполне логично, летним и зимним тропиками, так как эти линии отмечали две крайние точки годового пути Солнца и соответствовали в обитаемом мире Страбона летнему и зимнему сезону. Для Страбона летний тропик соответствовал максимальной высоте солнца и самому длинному дню года в Северном полушарии – летнему солнцестоянию; в этот момент на большей части обитаемого мира стояла жара. Позже этот тропик назвали тропиком Рака, так как в день солнцестояния на небе впервые появлялся Рак (лат. Cancer), четвертый знак зодиака. И любой житель Сиены знал, что во время летнего солнцестояния солнце стоит точно над головой, а указатель солнечных часов и гномон не отбрасывают тени. В этом факте сходилось большинство астрономов; его подтверждали Плиний и Арриан, ибо в Сиене «есть еще колодец, который отмечает летний тропик, по той причине, что район этот лежит под кругом тропика и потому гномоны в полдень не отбрасывают тени; ибо если ехать из наших мест, я имею в виду Грецию, на юг, то именно в Сиене солнце впервые будет у нас над головой и… его лучи также падают в колодцы до самой воды, даже если колодцы эти очень глубоки; ибо мы сами стоим перпендикулярно земле, и колодцы тоже копают перпендикулярно ее поверхности». В любое другое время тень гномона в Сиене падала «в сторону тьмы» и Полярной звезды и никогда в сторону равноденственного круга; это означало, что Сиена лежит на северном пределе солнечного подъема. В других же местах между Сиеной и экватором тень гномона падала иногда в одну сторону, иногда в другую, в зависимости от времени года. Кроме того, в любом из этих мест два дня в году солнце бывало точно над головой, а гномон не отбрасывал тени, и еще несколько дней так только казалось.

«Мы изготовим десять карт для Европы; мы изготовим четыре карты для Африки; для Азии мы изготовим двенадцать карт, чтобы включить ее всю…» Из описания карт Клавдия Птолемея, составленного около 150 г. н. э.
Вторая параллель, лежащая в Южном полушарии, – зимний тропик – была известна лишь теоретически. Наблюдения солнца в период зимнего солнцестояния проводились с большого расстояния: никто из греков не бывал в тех местах и не мог увидеть, как солнце проходит прямо над головой, и убедиться, что гномон не отбрасывает на землю тени. Было замечено, однако, что в день зимнего солнцестояния на горизонте впервые появляется Козерог (лат. Capricorn) – десятый знак зодиака. Так и получилось, что в последующих дискуссиях о тропиках в связи с положением различных мест и определением широт изучали всегда только летний тропик, лежащий в пределах обитаемого мира. Стандартным показателем широты стала длительность самого долгого дня в году, выраженная в часах; о длительности же самого короткого дня ничего не говорилось. Множество споров вызывал и вопрос о том, где именно следует поместить эти три параллели по отношению к известным пунктам на Земле, а следовательно – и на карте. Проблемой было также выяснить положение промежуточных линий (параллелей), если они находились слишком далеко друг от друга, чтобы непосредственно измерить расстояние. Еще один вопрос: как далеко один от другого расположены тропики и каково расстояние от каждого из них до экватора?
Астрономам известны были ответы на эти вопросы, так как они составляли основу исследований эклиптики – воображаемого большого небесного круга, названного так потому, что именно на нем происходили солнечные и лунные затмения. Эклиптику определяют по-разному, причем каждое из определений описывает одно или несколько следствий того факта, что ось Земли расположена под углом к оси небесной сферы. Точно так же проекция земного экватора на небесную сферу не совпадает с небесным экватором, а образует на ней наклонную окружность[14]; следовательно, плоскость эклиптики наклонена по отношению к плоскости небесного экватора.
Эклиптику определяют как проекцию видимого пути Солнца на небесную сферу – то есть как путь Солнца среди звезд[15]. Древним астрономам было очевидно, что плоскость эклиптики не совпадает с плоскостью земного экватора. Следовательно, ось Земли не может совпадать с осью небесной сферы. Самая понятная демонстрация наклона эклиптики – годовой путь Солнца; астрономы быстро поняли, что угол между эклиптикой и плоскостью экватора соответствует дуге между Солнцем в равноденствие и Солнцем на тропике Рака (в летнее солнцестояние) или Козерога (в зимнее солнцестояние). Греческие астрономы традиционно считали угол наклона эклиптики равным 24°. О том, каким образом был определен этот угол, ничего не говорится. Греческие математики получили эту же величину геометрическими способами. Они говорили, что угол наклона эклиптики равен углу, который образует в центре окружности сторона вписанного в окружность правильного пятнадцатиугольника – то есть 24°. Феон из Александрии утверждал, что Эратосфен оценил эту величину более точно; он утверждал, что угловое расстояние между двумя тропиками составляет 11/83 меридионального круга, или 47°42'40". Исходя из этого, угол наклона эклиптики, то есть угловое расстояние между экватором и любым из тропиков, составит половину этой величины, или 23°51'20". В реальности эта величина в то время должна была составлять 23°45'04". В настоящее время она составляет приблизительно 23°26'46"[16].
Определение астрономического положения тропиков ни в коем случае не решило проблемы установления широтных параллелей; тем не менее оно указало путь. Астрономы дали картографам первые три разделительные линии восток—запад, в буквальном смысле слова параллельные между собой, и установили пределы двух тропических (жарких) зон, или «климатов». С помощью их данных оказалось возможным определить теоретически местонахождение двух арктических (морозных) зон; своим происхождением эти зоны тоже обязаны астрономам, картографы же использовали их и нанесли на карту.
Ранние греческие астрономы использовали понятие «арктический круг» не в отношении морозных областей земли около полюсов; для них этот термин имел отношение к звездной сфере. Наш арктический, или полярный, круг – на карте и на земле – зафиксирован для удобства на широте 66°30'; в греческой же астрономии положение арктического круга менялось в зависимости от позиции наблюдателя и от его горизонта. На экваторе, например, арктического круга просто не было, так как все звезды Большой Медведицы опускались под горизонт. Не было его и в любой точке Южного полушария. Однако севернее экватора – в таких местах, как Александрия или Массалия, – арктический круг можно было определить как круг на небесной сфере, который включает в себя все незаходящие звезды, в том числе Полярную; другими словами, этот «круг» всегда касается горизонта наблюдателя (в точке севера)[17].
Следовательно, с продвижением наблюдателя к северу радиус арктического круга увеличивается. Кроме того, радиус арктического круга с Полярной звездой вблизи центра может служить указателем широты наблюдателя. Другими словами, при движении от экватора на север угловая высота Полярной звезды растет в той же пропорции, что и радиус арктического круга, так что на полюсе угловая высота Полярной звезды составит 90°, а окружность арктического круга будет равна окружности, касательной к горизонту под углом 24°[18].
По всей видимости, первым перенес арктический круг на землю Пифей в своем рассказе об острове Туле. Говоря о широте острова, он утверждает, что это самое северное населенное место, а арктический круг на Туле равновелик летнему тропику (тропику Рака). Это означает, что зенитное расстояние Полярной звезды на Туле такое же, как угловая высота летнего тропика над экватором, а именно – около 24°, и это есть примерное расстояние от полярного (арктического) круга до Северного полюса. Другими словами, если Пифей, подобно Эратосфену и Страбону, помещал летний тропик в 24° к северу от экватора, то широта Туле должна быть 66°, то есть дополнительной к широте летнего тропика.
У ранних греческих авторов и, разумеется, у Страбона можно встретить многочисленные упоминания «арктического круга» именно в смысле первого определения. Так, говоря о широте различных мест обитаемого мира, Страбон указывает: «Народ, производящий корицу, – первый, для кого Малая Медведица полностью находится внутри арктического круга и всегда видна; ибо яркая звезда на кончике хвоста, самая южная в этом созвездии, расположена там на самой окружности арктического круга и, соответственно, касается горизонта». Он мог бы сказать то же самое гораздо проще: высота Полярной звезды (широта) в стране, где рождается корица (Сомали), равняется длине Малой Медведицы, или составляет столько же градусов и минут дуги. Таким образом, тогда существовало два арктических круга: один из них был подвижен относительно земли и менялся в размере в зависимости от позиции наблюдателя, а второй – зафиксирован математически, как на современных картах. По всей видимости, в то время, когда Страбон изучал этот вопрос, широко использовались оба понятия.


