Анатолий Левенчук
Методология 2025

Полная версия

• Методологу надо рассмотреть альтернативы разложения метода для какой-то сигнатуры. Если у вас в системе предусмотрен метод «чистка зубов», то вам надо рассмотреть варианты еды на ночь семян кунжута (удивительно хорошая очистка!), использования зубной нити, зубочистки, зубной щётки или ультразвуковой щётки с выбором из многих видов зубной пасты и вариантами щёток (например, V-образная зубная щётка, если у вас брекеты), задействование ирригатора (чистка водой под давлением), и т.д.. Каждый метод обладает своими плюсами и минусами, а если это верхнеуровневый метод, то может быть реализован очень по-разному, его составляющие будут иметь в свою очередь, разные разбиения – и надо будет опять выбирать, и там, скорее всего, будут какие-то другие предметные области. Это и есть работа. По большому счёту, именно методолог делает «разузловку», разбиение системы на функциональные единицы. Понятно, что в силу разделения труда это очень плохо делать «сверху вниз», ибо ключевое понимание того, как же именно работает система, будет на нижних уровнях. Но это уже нюансы, о которых будет в курсе «Системная инженерия».

• Архитектор будет следить, чтобы в конструктивах, реализующих функциональные объекты с предложенными функциями/методами работы, не было лишних зависимостей и соблюдались приемлемые значения важных общесистемных архитектурных характеристик. Так, если коммуникация в организации идёт «через верх» (каскадирование: CEO сказал что-то замам, те выдали начальникам дирекций, те выдали начальникам отделов, те выдали начальникам секторов, те уже не стали подключать сотрудников и сами что-то сделали, потом пошло согласование этих предложений снизу вверх), то это будет дико медленно – цикл стратегирования, бюджетирования и т. д. будет легко длиться больше года, и когда будет какой-нибудь валютный или кадровый кризис, организация банально не сможет быстро отреагировать. Архитектор вмешается, заставит разработчиков организовать потоки работ как-то другим способом, методологи должны будут предложить методы стратегирования и бюджетирования, которые не будут подразумевать каскадирования (подробней об этом в курсе «Системный менеджмент»).

• Проектировщик/designer будет принимать решение по тому, что же из имеющегося в культуре разнообразия видов методов работы (и, соответственно, разнообразия ролей), предлагаемых методологом, должно войти в разрабатываемую систему, и какими видами конструктивов с их интерфейсами, удовлетворяющих ограничениям, полученным от архитектора, это может быть реализовано – и он также собирает и другие ограничения (технология изготовления, общая стоимость владения, компоновка и т.д.), чтобы выдать многоуровневое «изобретение».

Современная инженерия сложна, поэтому и происходит разделение труда: много лет назад все эти работы выполнялись (часто неосознанно) одной ролью «инженер» (или «менеджер», или «учитель» – названия тут могут быть самыми разными в зависимости от типа систем). А сегодня чаще всего в крупных проектах эти роли раздаются разным людям, при этом роль архитектора уже более-менее выделилась из роли разработчика, а вот роль методолога от роли проектировщика у разработчика только-только начала отделяться.

⠀

«Схемотехника»: представление метода работы графом потоков

А дальше можно сразу обратиться к традиционному представлению методов в виде функциональной диаграммы, часто называемой принципиальной схемой. Такие диаграммы разбирались в курсе «Системное мышление»: предметы метода текут/flow между создателями, которые меняют их состояния. Если это непрерывные потоки (поток/flow – это идентификация объекта на основе сохранения маршрута/пути, определение из ISO 81346:2022), то примеры сразу очевидны – методологи там называются «схемотехники», они строят принципиальные (принципиальность – это указание на функциональность, «метод работы», а не конструктивность) электрические схемы, радиотехнические схемы, но могут быть также и гидравлические схемы, и кинематические схемы и самые разные другие схемы.

• Так что очевидный следующий шаг в выражении методов – сразу пройти весь путь: от последовательностей/chains (последовательности методов, например, «стек» тут тоже последовательность вложений или последовательность использования, да и «шкала» – последовательность, упорядоченность в ряду объектов)

• к деревьям/trees (хорошо представимы разными MindMaps, которые легко сводимы к аутлайнам/outlines, по факту это «хорошо структурированное оглавление», где в листьях этого оглавления могут лежать какие-то более подробные описания, фреймворк Gielingh с диаграммами гамбургера как раз такой граф «почти дерева»),

• и далее к графам/graph как общей форме представления потоков чего бы то ни было – в том числе предметов метода между ролями, задействующими метод.

Примеры графовых визуальных представлений функционального (методов работы, время эксплуатации) описания системы были приведены в курсе «Системное мышление». Прикладных методологов самых разных предметных областей учат разрабатывать такого сорта визуальные представления, «принципиальные схемы». В электронике даже выделяют отдельную специальность «схемотехника»³², ибо речь идёт об электронных схемах и устройствах, описываемых такими схемами.

Потоковые (движение предметов метода по каким-то путям) представления, удобно представимые графом, распространены и в менеджменте. Фон Берталанфи выделял исследование потоковых представлений систем как «исследование операций» (operations research), речь шла о времени эксплуатации (operations) – и эта дисциплина легла затем в основу операционного менеджмента, логистики, теории массового обслуживания. Конечно, в исследованиях операций в основе лежали «работы», речь шла прежде всего о потоках ресурсов между рабочими станциями. Но это можно было представить и как специфически функциональное представление: «рабочая станция» – это ведь роль, её могут выполнять разные конструктивы, она может действовать разными методами (прикладными методами операционного управления!). Опять мы попадаем в то, что методология – фундаментальная дисциплина, и даже если речь идёт об управлении работами по методу, то это рассмотрение может быть функциональным, и тут методология будет задействована для разбирательства с работами и работниками как прикладная методология операционного менеджмента – несмотря на все предупреждения «не путать метод работы и работы по методу». Методы исследования операций, методы проектного управления работами, методы операционного управления – это всё методы, только ими занимается прикладная методология этих предметных областей.

С графами, которые описывают работы каких-то подсистем одного системного уровня по их взаимоувязанным методам (разложение методов одного системного уровня), есть разные ситуации их использования:

• Вы смотрите на них, как на «пассивную модель». Это означает, что интерпретатором модели является «тот, кто смотрит», алгоритм в вашей голове в виде программы «мастерство рассмотрения принципиальной схемы», а граф – данные для этой программы. Помним из курса «Рациональная работа», что модель – это программа, она исполняется, чтобы получить результат моделирования. Исполнитель программы, даже если он «просто смотрит на диаграмму» – тот, кто смотрит на эту диаграмму, и он также проводит с помощью диаграммы рассуждение, получает результат моделирования. Если нет рассуждения по диаграмме, то диаграмма не нужна. Когда вы пытаетесь разобраться в ходе ремонта «почему не работает», это как раз такая работа с графовым представлением разложения методов. Ваше мастерство проделывает рассуждения с описанием системы как графа связанных какими-то потоками предметов методов подсистем. Каждая из подсистем выполняет какие-то преобразования предметов метода, проводит их по состояниям, чтобы получить какой-то результат. Скажем, в логистической схеме – это работы по методам транспортировки и хранения предметов работ, а также работы по заказам партий предметов работ.

• Эта диаграмма – лишь визуальное представление графа потоков предметов методов, а вообще-то этот набор потоков представляется программой, решающей набор дифференциальных уравнений, описывающих взаимодействие подсистем в этом графе – «физику процесса». Расчёт по этой программе может провести компьютерная программа, «прогонять программу» (выполнять вычисления по алгоритму программы) будет уже компьютер, у которого эта программа – его «мастерство». Человеку остаётся лишь наблюдать результат прогона.

• В современных системах AI может быть ещё проще: вы можете показать компьютеру визуальную функциональную/принципиальную схему/диаграмму с заданными на ней какими-то функциональными характеристиками (скажем, на радиосхеме – входными напряжениями, номиналами резисторов и конденсаторов, транзисторов и катушек), а потом компьютер сам переведёт визуальную нотацию в программный код, отражающий какую-то систему дифференциальных уравнений и посчитает значения нужных характеристик (например, выходную мощность).

Увы, в курсах для архитекторов метод работы системы (в том числе системы-создателя) описывается в целом, без выделения специфической методологической/функциональной части. Да и в курсе для проектировщиков/designers не так много говорится про работу с функциями/методами, разве что упоминается, что проектирование надо начинать с работы с функциональными диаграммами. При этом функциональные диаграммы трудны для понимания, в них всё происходит как бы «одновременно», там законы типа закона Кирхгофа для электрических цепей. Помним, что разложения метода/функции тоже надо понимать, как работающие «одновременно». Но могут быть и всякие задержки и лаги (реактивные сопротивления в электроцепях, задержки на производство и логистику с момента выдачи заказа в цепях поставки, время продажи партии в розничных/retail сетях/chains).

В непрерывном производстве (нефтехимия, энергетика) функциональные диаграммы часто гибридны, в них приводится результат методологической работы (выбор метода) и одновременно указываются и результат проектирования: элементы конструкции. Это оформляется как P&ID диаграммы, piping and instrumentation diagram и PFD, process flow diagram диаграммами³³.

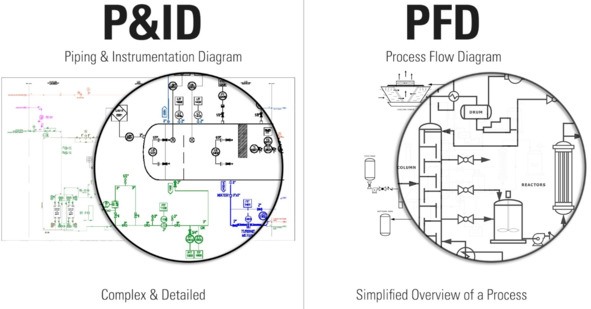
Каждый отдельный тип конструктива из крупной «нарезки на модули» архитекторами проектировщики будут потом в концепции системы упоминать не просто сам по себе, а как реализующий какую-то подсистему в её роли в системе.

Концепция системы часто представляется в форме какой-то гибридной диаграммы. В её основе часто – функциональная диаграмма (в системах функциональность – первична), но для функциональных объектов указано, какие конструктивные объекты будут играть эти роли, часто это делается «аннотированием» обозначений на «принципиальной схеме» указанием на то, какие конструктивы будут задействованы для воплощения этих функциональных объектов. Какого-то специального представления «отображения» функционального представления на конструктивное представление системы, например, таблицы соответствия, не делается. Иногда функциональные диаграммы в форме принципиальной схемы гибридизируются каким-то указанием разнесения её элементов на модули («функциональный насос» реализован «тремя конструктивными насосами и системой управления для них», это сделано для повышения надёжности), и часто ещё указывается и компоновка в пространстве, поэтому обозначение каких-то элементов делается состоящим сразу из нескольких имён, если это возможно: функциональное, конструктивное, пространственное и так далее (стандарт ISO 81346 как раз про правила такого именования, обозначений/designations).

Так что большая часть методологической работы часто делается сегодня в формате графовых представлений «принципиальных схем». Расчёты по таким функциональным диаграммам потоков жидкостей, электрического тока, энергии, даже денег, предметов работ, пассажиропотоков, а ещё потоков информации и т. д. учитывают «одномоментность во времени» и называются 1D-моделированием, ибо это одномерное представление – какая-то характеристика в каждом месте диаграммы разворачивается во времени.

Такое функциональное (это потоки в ходе функционирования моделируемой системы, функциональное представление – это ответ на вопрос «как работают в момент эксплуатации») моделирование чаще всего делают при помощи систем дифференциальных уравнений, учитывающих «одномоментность». Иногда такое физическое 1D моделирование называют системным моделированием, ибо речь идёт о моделировании работы системы как функционального объекта в целом на основе понимания того, как именно работают отдельные подсистемы.

В менеджменте такое моделирование чаще всего делают средствами системной динамики³⁴ – и это хорошо, только не надо считать, что это будет единственное моделирование в ходе проекта по созданию системы. Нет, это только 1D-моделирование, но будут ещё и другие. Более того, сегодня системным моделированием чаще называют 1D-моделирование не только упрощёнными дифференциальными уравнениями системной динамики (там очень ограниченный набор элементов модели и допустимых видов уравнений в системе дифференциальных уравнений), но и полноценным физическим описанием системы. В физическом системном моделировании (physical systems modeling), узко понимаемом как численное 1D моделирование, конкурируют каузальное моделирование с системой уравнений из обычных дифференциальных уравнений (ODE) и акаузальное моделирование с системой из алгебраических дифференциальных уравнений (ADE). Каузальное моделирование требует указывать порядок решения системы уравнений, а акаузальное моделирование – нет, систему уравнений решает сам компьютер, тренд при этом – переход от каузального моделирования к акаузальному.

Виды физического системного моделирования: функциональные диаграммы есть, но вместо них может быть компьютерный код

Текущий текст подраздела предназначен главным образом для «технарей», его может быть трудно одолеть людям, которые не имеют высшего инженерного образования. Но если вы «технарь», а текст плохо понятен – попробуйте пройтись по ссылкам на оригинальную литературу и хотя бы чуть-чуть её полистать. Всё-таки инженеров такому должны учить, и освежить эти знания никогда не поздно. Курс «Методология» – это курс вузовского уровня, делать из него «попсовый курс» без отсылок к физике и математике – неправильно.

1D-моделирование довольно долго делалось на акаузальных языках моделирования, например, Modelica³⁵, одновременно с графическим и текстовым представлением систем алгебраических дифференциальных уравнений. В физическом системном моделировании учитывается уже более-менее разная физика системы (механика, гидравлика, энерготеплопереносы и т.д.) или какие-то её другие свойства (например, умение производить работы, пропускать через себя поток предметов работ – иногда это называют даже factory physics). Но это всё моделирование функционирования, по факту – это моделирование метода работы системы. Вот пример представления модели на Modelica³⁶:

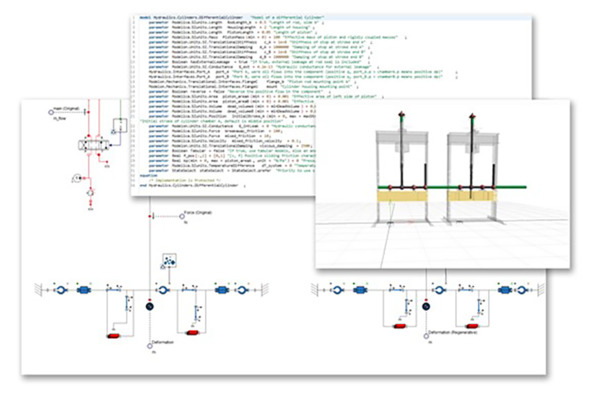
Мы видим на картинке 3D-модель системы «как в САПР», а также её функциональную графическую модель (диаграмму), а также программный код, соответствующий этой диаграмме. Диаграммное представление «наглядно», но с ним очень трудно работать – при росте размера диаграммы и увеличении числа «аннотаций» каждого элемента диаграммы (по факту «аннотации» – это текст, описывающий элементы диаграммы и связи – никогда не забываем, что любую картинку надо объяснять, и к картинкам для полной понятности мы «приговариваем» большое количество текста) модель, то есть систему дифференциальных уравнений, становится удобней представлять в виде текста на языке программирования. «Резистор» становится не схемным изображением на диаграмме, а текстом программы.

По итогам эксплуатации многочисленных систем с Modelica оказалось, что диаграммное представление функциональных схем менее удобно в работе: модельеры-проектировщики проводят много времени в текстовых представлениях, а диаграммы используют главным образом в «презентациях», для красоты, которую называют «наглядностью». Любые изменения-исправления, вставки и удаления, предложение альтернатив и комментарии делаются в текстовой форме, она банально удобнее. Поэтому современные средства 1D-моделирования по факту представляют собой пакеты численного моделирования для обычных языков программирования, например, один из самых мощных таких пакетов – JuliaSim³⁷. Отсутствие «визуальности» функционального моделирования с лихвой компенсируется удобством использования: тексты менять в ходе разработки много быстрее, чем диаграммы. И тексты можно пересылать друг другу, легко комментировать, чего не сделаешь с диаграммами – учитывая ещё и то, что откомментировать фрагмент текста программы функциональной модели можно и в чате, а вот с диаграммами всё не так просто, нужны специальные дорогие программы для работы с диаграммами, и они должны быть установлены у всех участников проекта, что обычно невозможно.

Тем самым мы от ограниченного диаграммного языка описания методов в их разложении перешли к описанию разложения метода алгоритмом, что ярко проявляется в функциональном физическом моделировании.

Инженеры в ходе проектирования обсчитывали принципиальные и технологические схемы, иногда называя это одноразмерным/1D моделированием, чтобы противопоставить трёхмерному прочностному и тепловому моделированию – речь-то идёт о функциональных описаниях, и тут у математиков, системных инженеров, программистов и всех остальных терминология существенно различается. Это как раз наша задача – ввести какой-то общий язык описания этого моделирования и этих вычислений, привязав эту терминологию и способы моделирования к современным методам разработки. «Хитрая физика» в функциональном физическом моделировании ведёт к «хитрой математике», которая ведёт к «хитрым языкам моделирования», которые реализуются достаточно необычными приёмами в разработке компиляторов и библиотек, поддерживающих моделирование в конкретных областях физики (электротехника, оптика, теплоперенос), но и не только физики – речь идёт вообще о моделировании мира в момент работы системы.

В традиционной «железной» инженерии принято было использование MatLab (более удобен для вычислительных задач, чем Фортран) и SimuLink для создания имитационных моделей, программные среды для вычислений с ODE (odinary differential equations in state space form – дифференциальные уравнения для пространства состояний входов и выходов). Это стало мейнстримом, но оказалось, что сопровождать модели в такой форме невозможно: для типовых случаев нельзя сделать библиотеки отдельных функциональных элементов, которые присутствуют в системе, и приходится каждый раз понимать, куда и как вписать очередное уточнение модели, или куда и как вписать очередное изменение модели.

Потому моделированию в ODE было противопоставлено акаузальное моделирование/acausal modeling с использованием DAE (differential algebraic equations) с алгебраическими переменными, которым a priori не могло быть придано никакого входного или выходного статуса – порядок вычислений не мог быть предсказан, ибо непонятно заранее, где у какого-то резистора вход, а где выход в составе модели.

Но как же проходит такой трюк с переходом от ODE к DAE? А вот так: разные уравнения собираются в большую систему из сотен, или даже тысяч (а в последнее время речь идёт и о миллионах) дифференциальных уравнений, и дальше решением этой огромной системы уравнений занимается компьютер (или даже суперкомпьютер, если система реально большая). Вот сравните удобство для инженеров моделирования электрического мотора с учётом инерции его вращения при представлении модели в DAE и ODE формах в их диаграммном виде³⁸:

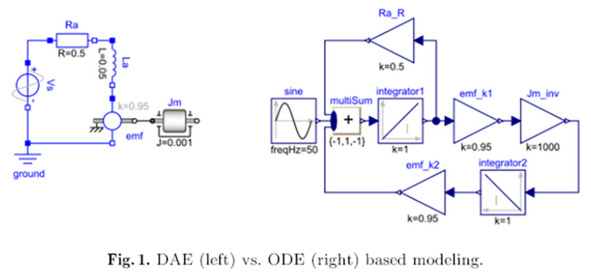
Первые принципы физики естественным образом приводят к рассмотрению акаузальных моделей с алгебраическими дифференциальными уравнениями (DAE), таких как на рис. 1 слева. Например, рассмотрим случай электрических цепей. Законы цепей, такие как законы Кирхгофа, естественно выражаются в виде уравнений баланса: алгебраическая сумма токов в сети проводников, встречающихся в одной точке, равна нулю; или сумма всех напряжений в петле равна нулю. Это верно будет и для операционного менеджмента (потоки работ, денег, материалов в сетях/цепях поставки), в любых других системах, в которых что-то «течёт» (в том числе и «текут данные»).

Аналогичным образом некоторые компоненты (например, резисторы или конденсаторы) имеют заранее определенную ориентацию входа/выхода. В одной и той же схеме можно назначить разный статус входа/выхода её переменным, в зависимости от того, какие из них объявлены источниками. Такая же ситуация возникает в механике или термодинамике, везде, где нужно функциональное моделирование значений каких-то характеристик во времени. Кроме того, добавление ещё одного физического компонента в принципиальную схему не представляет сложности, тогда как для «вычислительной блок-схемы» на рисунке справа может потребоваться полная переработка.

И в итоге были предложены специальные акаузальные (не требующие учёта порядка влияния друг на друга элементов через входы и выходы) языки программирования и вычислительные среды для них. Компания MathWorks к SimuLink с его ODE добавила SimScape с DAE, компания Siemens предлагает Amesim, но де-факто стандартом и экспериментальной средой для отработки новых идей стал язык акаузального имитационного моделирования мультифизики Modelica (https://modelica.org/), для которого было разработано полдюжины компиляторов самыми разными фирмами и университетами. На смену Modelica сейчас приходит проект JuliaSim с акаузальным инструментарием ModelingToolkit. jl³⁹.

Modelica с годами распухала: кроме мультифизики в него был добавлен аппарат моделирования машины состояний, и стало возможным выражать на нём и логику управления (кибер-часть функционального моделирования), то же самое происходило с другими системами моделирования.

А поскольку разнородных средств физического/имитационного моделирования оказалось очень много, для объединения самых разных моделей на уровне обмена данных между их входами и выходами был предложен стандарт FMI⁴⁰ (functional mock-up interface – он поддерживается более чем 150 программными инструментами для моделирования).

Но и DAE/acausal моделирование оказалось с проблемами. Главная проблема тут – невозможность использования Multi-Mode DAE Models (mDAE). Multi-mode models – это моделирование режимов, связанных с разными структурами одной и той же системы. Если у вас летит ракета с тремя ступенями, потом с двумя, потом с одной ступенью – моделировать это нужно по-разному, это же будут лететь совсем разные ракеты, у которых только название общее, а физика совсем разная! Если у вас моделируется атомный реактор в ходе его нормальной работы, то там одна физическая модель. А если он уже начал плавиться – то моделировать его плавление нужно по-другому, прошлая модель реактора не будет работать. Это явление носит разные имена, Multi-mode DAE models только одно из них, в математике и физике используют и другие, например, VSS (variable structure system, – и они тоже имеют много разных подвариантов, «частных случаев»)⁴¹. Есть и другие имена, разные группы исследователей приходят к этой проблеме учёта изменения структуры модели вслед за структурой моделируемой физической системы в разных исследовательских ситуациях и подчёркивают в имени разные аспекты проблемы.

Математика mDAE хитра, и языки акаузального физического моделирования и их компиляторы должны учитывать эту хитрость математики, иначе результаты моделирования будут кривые. Вот одна из работ 2020 года, проясняющая трудности: «The Mathematical Foundations of Physical Systems Modeling Languages»⁴². Трудности там демонстрируются на вот таком простом примере, с которым не справляются нынешние компиляторы Modelica, и дело там не только в computer science (плохом языке моделирования и плохом его компиляторе), но и в математической-физической стороне вопроса:

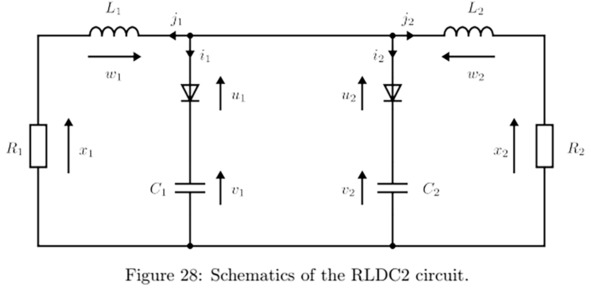
Схема выглядит очень просто, но её модель должна содержать по факту описание четырёх режимов работы – для ситуаций, когда диоды оказываются закрыты или открыты в разных сочетаниях. Поэтому существующие компиляторы на таких схемах спотыкаются – они часто интерпретируют их как «один режим работы», когда их там четыре.

После того, как разобрались с физикой и описывающей её математикой, подключается computer science, ибо нужно теперь создать язык с нужной для этой математики операционной семантикой и (оптимизирующий!) компилятор для него. Это оказывается в случае mDAE не так легко, ибо уже не хватает уровня продвинутости человечества в computer science. Исследования (computer science) и разработки (software engineering) для акаузального мультифизического моделирования идут по вот этим основным линиям, а основное развитие сейчас происходит в ModelingToolkit. jl⁴³ в проекте JuliaSim⁴⁴.

В какой-то мере этот тренд с использованием «языка» mDAE вместо ODE для физического моделирования похож на создание разных языков программирования для решения expression problem в самой computer science⁴⁵. Суть этой expression problem ровно в том же: разработка библиотек универсальных вычислительных элементов требует от языков программирования и реализующих их компиляторов возможности добавлять новые объекты для старых операций и новые операции для старых объектов, чтобы не нужно было переписывать весь код программы. Обратите внимание, что в предыдущем предложении мы по факту говорим, что языки программирования и языки моделирования – это одно и то же, функциональное моделирование делается на языке программирования. Это отдельная долгая история, ибо на самой заре программирования «языки высокого уровня» как раз и считались языками моделирования (например, Simula⁴⁶, первая версия которой появилась в 1962 году, это был первый объект-ориентированный язык). Это лишний раз подтверждает, что моделирование может и должно делаться не только на специализированных упрощённых языках моделирования, но и на самых обычных языках программирования общего назначения – но оно предъявляет специальные требования к этим языкам.

В mDAE против ODE мы расширяем expression problem с обсуждения только программных объектов и операций до обсуждения описания/моделирования физических сущностей: или ты делаешь язык, на котором разные функциональные объекты описываются разными наборами уравнений (декларативно), и просто добавляешь эти модели друг ко другу, или в языке у тебя такой возможности нет, и ты вынужден каждый раз переделывать программу при малейших изменениях моделируемой системы или малейших изменениях в идеях самого моделирования.

Если ты не решил эту «model expression problem», то тебе нельзя сделать стандартные библиотеки, оформляющие стандартные поведения функциональных объектов. Знания моделей становятся плохо переносимыми между моделями, модели плохо модифицируемыми – каждый раз при внесении изменений нужно переписывать и перекомпилировать всю модель.

Есть ещё и многомасштабность моделирования: объединение моделей разных системных уровней, разных масштабов времени, тут тоже свои математические и выразительные трудности в языках программирования⁴⁷, – и там тоже проблемы с ODE против DAE, плюс много чего собственного, и для этого тоже может потребоваться учёт в языках программирования/моделирования. Увы, языки программирования/моделирования не системны/многомасштабны «из коробки».

Для моделирования в реальном времени (цифровой двойник/digital twin, скорость моделирования имеет значение, проблемы алгоритмики как алгоритмов, дающих при заданной точности вычислений максимальную скорость счёта, тут всплывают в полной мере) тоже есть множество проблем, например, высокая скорость получается за счёт различных суррогатов⁴⁸ моделей (быстрых аппроксиматоров сложных функций, например, нейросуррогаты получаются на базе нейронных сетей). No free lunch theorem гласит, что нет универсально быстрых алгоритмов: алгоритм, хороший для одной задачи будет плох для другой, и наоборот. И в каждом «общем решении» всё равно будут возникать (сотнями, тысячами!) многочисленные «частные случаи», требующие отдельных способов решения. Обсуждение качественного имитационного/simulations моделирования обычно связывают с суперкомпьютерами, это не случайно. Для удешевления и ускорения моделирования нужно делать прорывы в алгоритмике, менять физику компьютера (например, переходить к оптическим или квантовым вычислениям).

Когда директор стадиона обсуждает цифрового двойника для своего стадиона, хорошо бы, чтобы он понимал SoTA в области моделирования. А то ему теоретики-математики без понимания сути computer science намоделируют так, что мало никому не покажется – моделирование тут похоже на безопасность, про него ведь можно легко сказать «моделирования много не бывает», и тогда оно может съесть все деньги и ничего не дать взамен, как и излишняя безопасность. Лекарство легко может стать болезнью.