Равиль Ильгизович Мухамедиев
Введение в машинное обучение

2.5. Контрольные вопросы

Что такое объект в задачах машинного обучения?

Как в общем виде записать функцию стоимости в задаче классификации?

Как в общем виде записать функцию стоимости в задаче регрессии?

Приведите выражение для функции гипотезы линейной регрессии одной переменной.

Как вычислить значения коэффициентов линейной регрессии? Укажите оба способа вычисления.

Приведите выражение функции стоимости логистической регрессии. Каково будет значение функции стоимости, если y = 0, h = 0, m = 2?

Каково назначение регуляризации?

Каковы недостатки логистической регрессии?

Какие алгоритмы применяются для минимизации значения функции стоимости логистической регрессии?

Чем отличается сигмоидальная функция от логистической?

Какие значения принимает логистическая функция?

2.6. Искусственные нейронные сети

2.6.1. Вводные замечания

Искусственные нейронные сети (Artificial Neural Networks – ANN – ИНС) – аппарат, который активно исследуется начиная с 40-х годов прошлого столетия. ИНС как часть теории коннективизма прошли значительный путь от эпохи завышенных ожиданий, через период разочарований (в 70-х годах) до широко применяемой технологии в настоящее время. Связь между биологическими нейронами и возможностями их моделирования с помощью логических вычислений установлена в работе Warren S. McCulloch, Walter Pitts [^[39]], в работе Розенблатта [^[40]] описана модель персептрона. Недостатки однослойного персептрона отражены в книге М. Минского и С. Пейперта [^[41], ^[42]]. В этой книге подробно рассмотрены ограничения однослойной нейронной сети и доказано, что она не способна решать некоторые классические логические задачи, в частности, обозначена знаменитая проблема неразрешимости функции XOR для однослойной нейронной сети. Преодолеть этот недостаток можно было путем использования многослойных нейронных сетей. Однако в конце 60-х годов было еще неясно, как обучать многослойные нейронные сети.

В 1974 году был предложен алгоритм, который впоследствии получил название «алгоритм обратного распространения» (backpropagation) [^[43], ^[44]], или «алгоритм обратного распространения ошибки», пригодный для автоматического подбора весов (обучения) многослойного персептрона или многослойной нейронной сети прямого распространения. Этот алгоритм стал базой для бурного развития нейросетевых методов вычислений.

Примечание. Первенство в разработке алгоритма окончательно не установлено. Считается, что он был впервые описан А. И. Галушкиным и независимо Полом Вербосом в 1974 году. Далее алгоритм развивался усилиями как отечественных ученых, так и зарубежных групп, которые, собственно, и ввели термин backpropagation в 1986 году. Метод несколько раз переоткрывался разными исследователями.

Значительный вклад в теорию коннективизма внесли советские и российские ученые [^[45], ^[46], ^[47], ^[48]], доказавшие возможность решения классических вычислительных задач в нейросетевом базисе, тем самым заложив фундаментальную основу построения нейрокомпьютеров.

Примечание. Коннективизм или коннекционизм – это подход к изучению человеческого познания, который использует математические модели, известные как коннекционистские сети или искусственные нейронные сети. Часто они бывают в виде тесно связанных между собой нейронных процессоров [^[49]].

Наиболее популярная архитектура ANN – сеть прямого распространения, в которой нелинейные элементы (нейроны) представлены последовательными слоями, а информация распространяется в одном направлении (Feed Forward Neural Networks) [^[50]]. В 1989 году в работах G. Gybenco [^[51]], K. Hornik [^[52]] и др. показано, что такая сеть способна аппроксимировать функции практически любого вида. Однако в тот период теоретическая возможность была существенно ограничена вычислительными мощностями. Преодолеть этот разрыв удалось в 90-х годах, когда были предложены сети новой архитектуры, получившие впоследствие название глубоких нейронных сетей. В результате в последние годы получены впечатляющие результаты в разработке и применении новых классов сетей и так называемого глубокого обучения [^[53]], которые состоят из множества слоев разного типа, обеспечивающих не просто классификацию, но, по существу, выявление скрытых свойств объектов, делающих такую классификацию высокоточной. Общее количество различных классов нейронных сетей превысило 27 [^[54]]. Введение в новые архитектуры сетей приведено в разделе «Глубокое обучение».

Применение аппарата ANN направлено на решение широкого круга вычислительно сложных задач, таких как оптимизация, управление, обработка сигналов, распознавание образов, предсказание, классификация.

2.6.2. Математическое описание искусственной нейронной сети

Рассмотрим ANN с прямым распространением сигнала. В такой сети отдельный нейрон представляет собой логистический элемент, состоящий из входных элементов, сумматора, активационного элемента и единственного выхода (рисунок 2.7).

Рисунок 2.7. Схема классического нейрона

Выход нейрона определяется формулами:

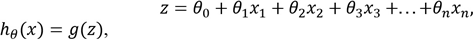
где g(z) – сигмоидальная функция.

Выражение функции гипотезы классического нейрона идентично выражению функции гипотезы логистической регрессии (Eq. 2.9).

Часто в качестве активационной функции применяется сигмоидальная функция, описанная в разделе «Логистическая регрессия».

В последнее время в литературе веса θ нейронной сети чаще обозначают символом w, подчеркивая тем самым преемственность естественных нейронных сетей и искусственных нейронных сетей, где широко используется понятие синаптического коэффициента или веса (weight). Кроме того, такое обозначение показывает разницу между множеством параметров или весов (W) и гиперпараметрами модели. Гиперпараметры определяют общие свойства модели, и к ним относят коэффициент обучения, алгоритм оптимизации, число эпох обучения, количество скрытых слоев сети, количество нейронов в слоях и т.п.

Для упрощения схемы сумматор и активационный элемент объединяют, тогда многослойная сеть может выглядеть так, как показано на рисунке 1.5. Сеть содержит четыре входных нейрона, четыре нейрона в скрытом слое и один выходной нейрон.

На рисунке входные нейроны обозначены символом х, нейроны скрытого слоя – символами a₁^[1], a₁^[1], a₂^[1], a₃^[1], a₀^[1] и выходного слоя – символом a₁^[2]. Если нейронная сеть имеет несколько слоев, то первый слой называют входным, а последний – выходным. Все слои между ними называются скрытыми. Для нейронной сети с L-слоями выход входного или нулевого слоя нейронов определяется выражением a^[0] = x.

На входе следующего или первого скрытого слоя имеем

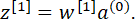
Выход первого слоя:

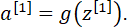
Для любого нейрона j, находящегося в скрытом слое i:

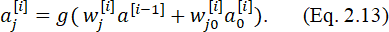
В этом выражении значение bias и его вес упомянуты отдельно как произведение ,

где w_j^[i] – вектор весов нейрона j.

Для выходного слоя:

Например, для сети на рисунке 2.8 выход каждого нейрона скрытого слоя можно рассчитать так же, как и для одиночного нейрона:

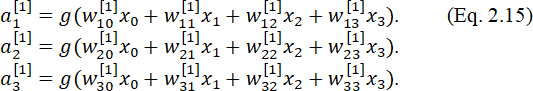
Выход нейронной сети определяется выражением:

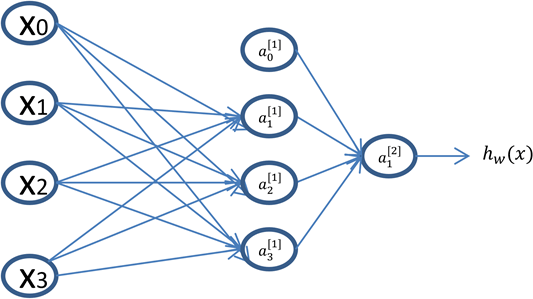
Рисунок 2.8. Схема многослойной сети с одним скрытым слоем

Для настройки весов w нейронной сети (обучения сети) используют функцию стоимости, напоминающую функцию стоимости для логистической регрессии (Eq. 2.12).

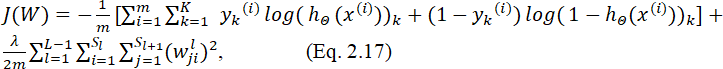
где L – количество слоев нейронной сети; s_l – количество нейронов в слое l; K – количество классов (равно количеству нейронов в выходном слое); W – матрица весов.

Достоинством нейронной сети является возможность классификации c несколькими классами. В случае классификации объектов одного класса, то есть тогда, когда мы должны отделить условно «положительные» объекты от всех остальных, количество нейронов в выходном слое может быть равным и 1 (рисунок 1.5). В этом случае принадлежность объекта к классу «положительных» определяется значением функции гипотезы, то есть если h_Θ(x⁽ⁱ⁾) > 0.5, то объект принадлежит к искомому классу. Однако чаще, в том числе с целью унификации, используется метод голосования («победитель забирает все»), когда сеть имеет в выходном слое 2 нейрона для двух классов объектов (рисунок 1.6), три для трех и т.д.

Рисунок 2.9. Схема многослойной сети с двумя выходами

Для обучения, то есть минимизации функции ошибки многослойной ИНС, используют алгоритм обратного распространения ошибки (Backpropagation of errors – BPE) [^[55]] и его модификации, направленные на ускорение процесса обучения.

2.6.3. Алгоритм обратного распространения ошибки

Суть алгоритма BPE заключается в следующем. Для тренировочного набора примеров

устанавливаем выход первого слоя нейронов:

Шаг 1. Выполняем этап прямого распространения сигнала по слоям сети, то есть вычисляем сигнал на выходе сети, выполняя расчет для каждого нейрона в каждом слое, как показано в выражениях 1.4, 1.5. Результаты в виде выходных значений нейронов сети a^[0],a^[1],…,a^[L] сохраняем в промежуточном хранилище (кэш).

Шаг 2. Используя полученный результат на выходе сети a^[L] = h_w⁽ⁱ⁾ (x), и необходимое для данного примера выходное значение y⁽ⁱ⁾, рассчитываем ошибку выходного слоя:

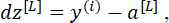
где L – номер выходного слоя нейронной сети.

Шаг 3. «Возвращаем» ошибку, распространяя ее обратно по сети с учетом значения производной:

где знак * – символ поэлементного умножения; g' – производная.

Производная сигмоидальной активационной функции:

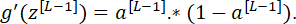
Для любого скрытого слоя сети:

В случае сигмоидальной активационной функции:

Рассчитанное значение градиентов ошибки dz^[1], dz^[2], … , dz^[L] также сохраняем в кэше.

Шаг 4. Модифицируем веса сети с учетом значения ошибки для всех слоев I ∈ L:

где i – номер слоя сети; ρ – параметр обучения (learning rate) (0 < ρ < 1); Θ⁽ⁱ⁾ – матрица весов слоя i; dz^[i] – рассчитанное значение ошибки i-го слоя (точнее говоря, градиент ошибки).

Получив измененные значения весов, повторяем шаги 1–4 до достижения некоторого минимального значения ошибки либо заданное количество раз.

Процесс обучения искусственной нейронной сети можно представить в виде следующей схемы (рисунок 2.10):

Рисунок 2.10. Итеративный процесс обучения искусственной нейронной сети

Рассмотрим пошаговый пример расчета прямого распространения сигнала, обратного распространения ошибки и коррекции весов.

Пошаговый пример расчета алгоритма обратного распространения ошибки

В этом примере (рисунок 2.11) веса нейронной сети будем обозначать символом w, смещения b. Номер слоя, как и ранее, указываем верхним индексом в квадратных скобках для того, чтобы не путать с индексом обучающего примера, номер нейрона в слое – нижним индексом. Выход нейрона по-прежнему обозначаем символом а.

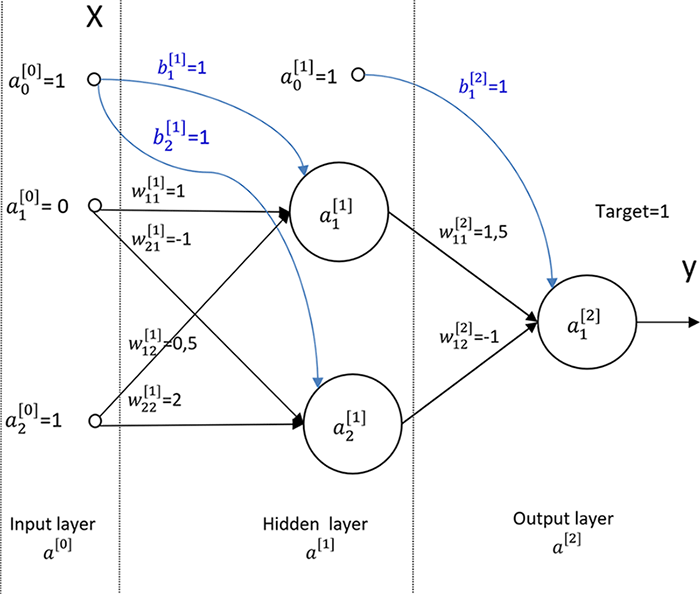
Рисунок 2.11. Пример нейронной сети с одним скрытым слоем

Входной слой с его входами x для единообразия последующих матричных операций обозначаем как нулевой слой – a^[0]. В нашем примере x1 = 0, x2 = 1, тогда a₁^[0] = x1 = 0 и a₂^[0] = x2 = 1. Смещение (bias) во всех слоях a₁^[l] = 1.

На вход сети, таким образом, подается вектор [1,0,1], а на выходе сети необходимо получить y=1.

Шаг 1. Прямое прохождение сигнала.

Рассмотрим прямое прохождение сигнала от входа к выходу:

Выход нейронной сети:

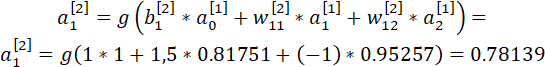
Шаг 2. Расчет ошибки выходного слоя.

Сеть должна давать значение y⁽¹⁾ = 1, однако получена величина 0.78139. Ошибка, c которой сеть «предсказывает» наш единственный пример, равна разнице между ожидаемым значением и полученным результатом.

Шаг 3. Обратное распространение ошибки.

Полученную ошибку нужно «распространить обратно» для того, чтобы скорректировать веса сети. Для этого рассчитаем градиенты ошибок нейронов скрытого слоя, используя выражение

Получим

Теперь у нас все готово для того, чтобы, используя градиенты ошибок, пересчитать веса нейронной сети.

Шаг 4. Коррекция весов нейронной сети.

Установим для нашего учебного примера большой коэффициент обучения (learning rate) ro = 0.5. Отметим, что в реальных случаях ro редко превышает 0.1. Здесь мы использовали относительно большое значение, чтобы увидеть значимые изменения весов уже на первой итерации.

Используем выражение (Eq. 2.18) для расчета измененных весов сети:

для скрытого слоя:

Используя скорректированные значения весов, повторим расчет прямого прохождения сигнала и получим значение ошибки выходного слоя:

Видно, что ошибка стала значительно меньше.

После третьей итерации dz₁^[2] = 0.14184

Примечание. Расчет двух итераций алгоритма BPE с применением Python-numpy приведен в MLF_Example_Of_BPE – https://www.dropbox.com/s/tw6zwht3d5pd4zf/MLF_Example_Of_BPE.html?dl=0

Пример, приведенный выше, является иллюстрацией прямого и обратного хода алгоритма так, что каждый обучающий пример и каждый синаптический коэффициент рассчитываются по отдельности. На практике этапы алгоритма для сети из L-слоев реализуются в матричном виде следующим образом:

…

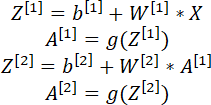
где W^[i] – матрица весов i-го слоя нейронной сети; X – матрица обучающих примеров размерностью n x m (n – число параметров, m – количество обучающих примеров).

Расчет алгоритма градиентного спуска для нейронной сети в матричном виде:

…

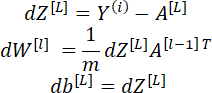
Примечание. Важно отметить, что алгоритм обратного распространения «требует», чтобы начальные значения весов были небольшими случайными величинами. То есть начальная инициализация требует нарушения «симметрии» для того, чтобы нейроны сети изменяли свои веса «индивидуально». Нулевые значения неприемлемы, поскольку градиент ошибки также будет нулевым и веса не будут корректироваться. Большие значения, сравнимые по величине со значениями, подаваемыми на вход сети, приведут к тому, что алгоритм не будет сходиться. Приведенный выше пример начальных значений весов и смещений является исключительно учебным.

Выражения, приведеные выше, говорят о том, что на вход сети подаются все обучающие примеры «одновременно» и значения градиентов ошибки рассчитываются сразу для всех примеров. Этот процесс составляет одну эпоху обучения. Batch Gradient Descent – это процесс обучения, когда все обучающие примеры используются одновременно. Нескольких десятков или сотен эпох обычно достаточно для достижения оптимальных значений весов матриц W^[i].

Однако, когда количество примеров очень велико, примеры разбиваются на группы, которые можно поместить в оперативную память компьютера, и эпоха обучения включает последовательную подачу этих групп. При этом возможны два подхода [^[56]]:

Stochastic Batch Gradient Descent – когда группа включает лишь один пример, выбираемый случайно из множества обучающих примеров.

Mini Batch Gradient Descent – когда группа включает некоторое количество примеров.

Примечание. Для ускорения обучения рекомендуется подбирать размер группы равный степени двойки – 8, 16, 32, …, 1024 – в идеале так, чтобы пакет примеров мог быть помещен в кэш-память процессора.

При применении современных пакетов машинного обучения программисту не приходится заботиться о выполнении алгоритма BPE. Он реализуется путем выбора того или иного оптимизационного алгоритма (solver). Часто применяются lbfs, adam. Например, загрузка многослойного персептрона (multilayer perceptron – MLP) и создание объекта классификатора осуществляются следующим образом:

from sklearn.neural_network import MLPClassifier

clf = MLPClassifier(hidden_layer_sizes = [10, 10], alpha = 5, random_state = 0, solver='lbfgs')

Пример применения MLPClassifier приведен в разделе 2.8 Пример простого классификатора.

2.6.5. Активационные функции

Нелинейная активационная функция играет фундаментальную роль в процессе обучения нейронной сети. Именно ее применение позволяет нейронной сети обучаться сложным закономерностям, содержащимся в исходных данных. Кроме уже упомянутой сигмоидальной функции часто используются и несколько других активационных функций (рисунок 2.12), описываемых уравнениями

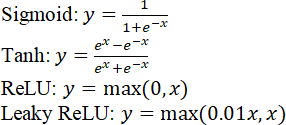
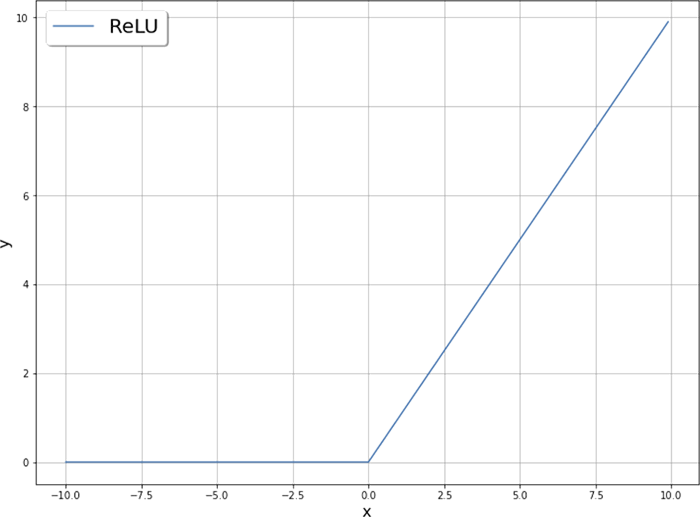
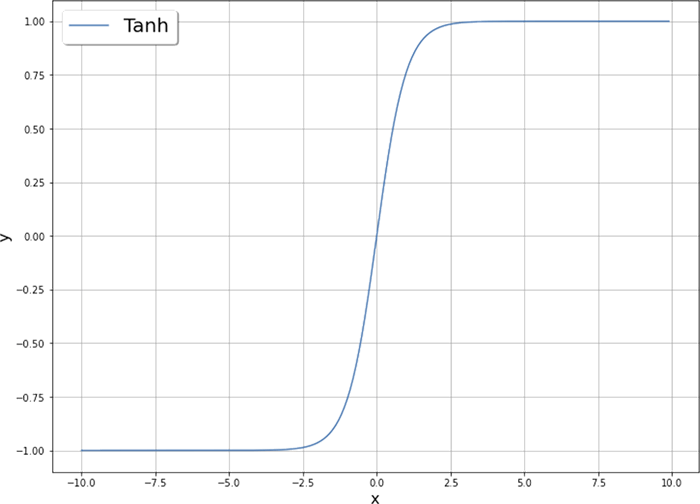
Рисунок 2.12. Активационные функции, применяемые в нейронных сетях

Резонный вопрос: «Почему исследователи используют несколько видов активационных функций?» Ответ, следующий: вычислительные затраты на расчеты результатов весьма велики, особенно в крупномасштабных сетях. Как известно, расчет выхода каждого слоя нейронной сети выполняется с использованием активационной функции. А в процессе выполнения алгоритма обратного распространения ошибки используется производная активационной функции. И в том, и в другом случае ReLU имеет большое преимущество с точки зрения вычислительных затрат. Следовательно, нейронная сеть будет обучаться значительно быстрее. С другой стороны, использование сигмоидальной функции для выходного слоя нейронной сети позволяет вычислять оценку вероятности принадлежности к классу, поскольку она принимает значения в диапазоне от 0 до 1.

2.7. Контрольные вопросы

Какие ученые оказали существенное влияние на развитие коннективизма?

Коннективизм или коннекционизм – в чем отличие этих двух терминов?

Приведите схему классического нейрона.

Приведите схему многослойной сети прямого распространения.

Как вычисляется выход многослойной нейронной сети прямого распространения?

Приведите функцию стоимости многослойной сети прямого распространения.

Сколько основных шагов в алгоритме обратного распространения? В чем их назначение?

Каково назначение кэша в процессе выполнения алгоритма обратного распространения ошибки?

Что такое эпоха обучения нейронной сети?

Укажите, какие виды процессов обучения нейронной сети применяются на практике.

В чем заключается сходство и отличие активационных функций, применяемых в нейронных сетях?

В чем заключается сходство активационных функций, применяемых в нейронных сетях?

В чем заключается преимущество активационной функции ReLU?

Какая активационная функция удобна для реализации бинарного классификатора?

Какими должны быть начальные значения весов и смещений в нейронной сети?

2.8. Пример простого классификатора

Рассмотрим интересную задачу классификации изображений, представленную в качестве примера применения TensorFlow [^[57]]. TensorFlow в нашем решении мы используем лишь для загрузки данных, а в качестве классификатора применим упомянутый выше MLPClassifier. Суть задачи заключается в том, что необходимо классифицировать предметы одежды по их монохромным изображениям в низком разрешении (28 х 28). Набор данных Fashion-MNIST содержит 60 000 изображений для обучения и 10 000 для тестирования, начиная от футболок и брюк и заканчивая сумками и туфлями. Всего 10 классов изображений. Классы, пронумерованные от 0 до 9, и их описание показаны на рисунке 2.13.

Рисунок 2.13. Образцы Fashion-MNIST

Fashion-MNIST разработан в дополнение к классическому набору данных MNIST, который часто используют как «Hello, World» для отладки методов машинного обучения в задачах компьютерного зрения. MNIST содержит изображения рукописных цифр (0, 1, 2 и т.д.) в формате, идентичном формату изображений одежды набора Fashion-MNIST. Для современных программ компьютерного зрения MNIST стал «слишком прост», поэтому применение более сложного набора данных полезно для отладки систем машинного обучения.

Загрузить набор данных можно, используя keras. Предварительно потребуется загрузить необходимые библиотеки:

# TensorFlow и tf.keras

import tensorflow as tf

from tensorflow import keras

# Вспомогательные библиотеки

import numpy as np

import matplotlib.pyplot as plt

Теперь можно загрузить набор данных и посмотреть одно из изображений:

fashion_mnist = keras.datasets.fashion_mnist

(X_train1, y_train),(X_test1,y_test)= fashion_mnist.load_data()

plt.figure()

plt.imshow(X_train1[10])

plt.colorbar()

plt.grid(False)

plt.show()

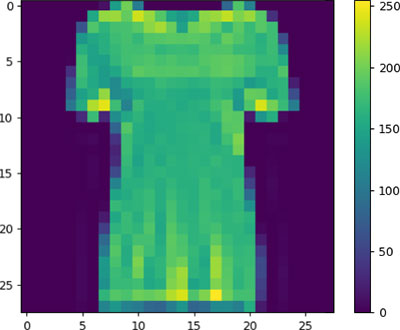
Как видно, диапазон изменения яркости пикселя – от 0 до 255. Если подать такие значения на вход нейронной сети, качественные результаты классификации существенно упадут. Поэтому все значения нужно нормировать так, чтобы на вход сети поступили значения в диапазоне от 0 до 1, просто разделив каждое значение на 255:

X_train1=X_train1/255.0

X_test1=X_test1/255.0

Следующее, что нам необходимо сделать в процессе предобработки, – это преобразовать двумерные массивы изображений 28 x 28 в одномерные векторы. Каждый такой вектор станет набором входных параметров размерностью 784:

X_train=np.reshape(X_train1,(X_train1.shape[0],X_train1.shape[1]*X_train1.shape[2]))

X_test=np.reshape(X_test1,(X_test1.shape[0],X_test1.shape[1]*X_test1.shape[2]))

В результате матрица X_train размерностью (60 000, 28, 28) будет преобразована в матрицу размером (60 000, 784), которую можно подать на вход нейронной сети для тренировки.

from sklearn.neural_network import MLPClassifier

clf = MLPClassifier(hidden_layer_sizes = [15, 15,],

      alpha = 0.01,random_state = 0,

      solver='adam').fit(X_train, y_train)

Обучение нейронной сети может занять несколько минут. Затем можно оценить качественные показатели классификатора командами:

predictions=clf.predict(X_test)

print('Accuracy of NN classifier on training set: {:.2f}'

    .format(clf.score(X_train, y_train)))

print('Accuracy of NN classifier on test set: {:.2f}'

    .format(clf.score(X_test, y_test)))

print(classification_report(y_test,predictions))

matrix = confusion_matrix(y_test, predictions)

print('Confusion matrix on test set\n',matrix)

Значение accuracy может быть примерно следующим:

Accuracy of NN classifier on training set: 0.89

Accuracy of NN classifier on test set: 0.86

Изменяя количество нейронов в слоях сети и параметр регуляризации alpha (например, hidden_layer_sizes = [75, 75], alpha = 0.015), можно несколько улучшить результат:

Accuracy of NN classifier on training set: 0.91

Accuracy of NN classifier on test set: 0.88

Примечание. Программу данного раздела MLF_MLP_Fashion_MNIST_001.ipynb можно получить по ссылке – https://www.dropbox.com/s/ryk05tyxwlhz0m6/MLF_MLP_Fashion_MNIST_001.html?dl=0