Равиль Ильгизович Мухамедиев
Введение в машинное обучение

1.4. Контрольные вопросы

1. Искусственный интеллект – это часть обширного направления, называемого «искусственные нейронные сети»?

2. Глубокое обучение как направление исследований и разработок – часть машинного обучения?

3. Чем отличаются алгоритмы «обучения с учителем» от кластеризации?

4. Что такое линейный классификатор и чем он отличается от нелинейного?

5. Процесс настройки модели машинного обучения – это _____?

6. Укажите типы машинного обучения, относящиеся к классу «обучение с учителем» (Supervised Learning).

7. Какие библиотеки машинного обучения используются в данном пособии?

8. Укажите типы машинного обучения, относящиеся к классу «обучение без учителя» (Unsupervised Learning).

9. Вы получили заданный набор обучающих данных. Что делать, если результаты работы алгоритма машинного обучения не удовлетворяют потребностям практики?

2. Классические алгоритмы машинного обучения

2.1. Формальное описание задач машинного обучения

Формальная постановка задачи машинного обучения (задача обучения по примерам или задача обучения с учителем) заключается в следующем [^[35]].

Пусть имеются два пространства: Ob (пространство допустимых объектов), Y (пространство ответов или меток) и (целевая) функция.

Определено отображение y: Ob → Y, которое задано лишь на конечном множестве объектов (обучающей выборке (прецедентах) (sample set)) размером m:

то есть известны метки объектов ob₁, ob₂,…, ob_m. Требуется построить алгоритм A («обучить»), который по объекту ob определяет значение y(ob) или «достаточно близкое» значение, если допускается неточное решение.

Другими словами, зная значения целевой функции на обучающей выборке, требуется найти удовлетворительное приближение к ней в виде А.

При конечном множестве Y = {1, 2,…, l} задачу называют задачей классификации (на l непересекающихся классов). В этом случае можно считать, что множество X разбито на классы C₁,…, C_l, где Ci = {ob Ob | y(ob) = i} при i{1, 2,…, l}:

Ob = ⋃¹_i=1 C_i.

При Y = {(α1,…,αl ) |α1,…,αl {0,1 говорят о задаче классификации на l пересекающихся классов. Здесь i-й класс – Ci = {ob Ob | y(ob) = (α1,…,αl), αi = 1}.

Для решения задачи, то есть поиска оптимального алгоритма A, вводится функция потерь или функция стоимости (cost function) J(A(ob), y(ob)), которая описывает, насколько «плох» ответ A(ob) по сравнению с верным ответом y(ob). В задаче классификации можно считать, что

а в задаче регрессии

J(A(ob), y(ob)) = | A(ob) – y(ob) |

или

J(A(ob), y(ob)) = (A(ob) – y(ob))2.

Возникает закономерный вопрос: что же такое объект? В задачах машинного обучения объект – это некоторое множество параметров (признаков). Если некоторую сущность можно описать конечным набором параметров, то она может рассматриваться как объект в машинном обучении, причем ее физическая природа не имеет значения. Параметры могут задаваться исследователем, исходя из его представлений о наилучшем описании объекта, так, как это делается в «классических» задачах машинного обучения, или, с другой стороны, формироваться путем выполнения некоторой процедуры так, как это делается в глубоком обучении.

Таким образом, каждый объект ob описывается конечным набором (входных) параметров или свойств (input values or features) x₁,x₂,….x_n, одинаковым для каждого ob_i ∈ Ob , а y называется целевой переменной (целевым параметром) (target value) в задаче регрессии или классом в задаче классификации.

Алгоритм А может описываться конечным набором параметров θ_i ∈ θ или, как часто говорится при описании нейронных сетей, весов (weights) w_i ∈ W.

Задача обучения по примерам рассматривается как задача оптимизации, которую решают путем настройки множества параметров θ алгоритма А так, чтобы минимизировать значение функции стоимости J(θ) по всем примерам m.

В задаче регрессии алгоритм A часто называется функцией гипотезы, а функция стоимости определяется как сумма квадратов разности «предсказываемого» алгоритмом (функцией гипотезы) значения и реального значения у по множеству примеров m. При этом подбирается такая функция гипотезы h_θ(x), которая при некотором наборе параметров θ_i ∈ θ обеспечивает минимальное значение J(θ).

где m – множество обучающих примеров или объектов; x⁽ⁱ⁾ – значение параметров или свойств для i-го объекта; y⁽ⁱ⁾ – фактическое значение объясняемой или целевой переменной для i-го примера; h_θ – функция гипотезы, которая может быть линейной (h_θ = θ₀ + θ₁x) или нелинейной (например, квадратичная функция гипотезы одной переменной – (h_θ = θ₀ + θ₁x + θ₂x²).

Например, если мы рассматриваем задачу прогнозирования стоимости автомобиля, исходя из года его производства, то год производства будет являться входной переменной или свойством (x), а стоимость – целевой переменной (y) (рисунок 2.1).

Рисунок 2.1. Зависимость стоимости автомобиля от года выпуска

В таком случае мы решаем задачу регрессии одной переменной. Случай регрессии многих переменных возникает тогда, когда мы будем учитывать кроме года выпуска объем двигателя, количество посадочных мест, марку и т.п. Перечисленные параметры образуют множество свойств или входных параметров, которые определяют единственную целевую переменную – стоимость.

Забегая вперед, можно сказать, что для подбора параметров θ_i необходимо, чтобы параметры x_j∈X (в многомерном случае), описывающие объекты, были выражены единицами одинаковой размерности и примерно одинаковой величины. Чаще всего путем нормализации стремятся представить все параметры в виде чисел в диапазоне 0≤x≤1 или –1≤x≤1. Вообще говоря, выбор функции нормализации зависит от класса задачи. Кроме того, в процессе предварительной обработки данных могут быть использованы методы, обеспечивающие исключение аномальных значений, исключение шумов (например, высокочастотных) путем сглаживания и т.п. Выбор этих методов также зависит от класса задачи. После того как параметры нормализованы и очищены от аномальных значений, а также исключены объекты, которые определены не полностью (то есть объекты, для которых часть свойств неизвестна), выполняется поиск функции гипотезы h_θ(x), которая минимизирует стоимость J(θ).

2.2. Линейная регрессия одной переменной

Задача линейной регрессии формулируется как поиск минимальной функции стоимости (см. формулу 2.1) при условии, что функция гипотезы является линейной h_θ = θ₀ + θ₁x. Очевидно, что подобная функция соответствует линии в двумерном пространстве (рисунок 3.1a). Для нахождения оптимальной функции h_θ(x) применяется алгоритм градиентного спуска (gradient descent), суть которого заключается в последовательном изменении параметров θ₀, θ₁ с использованием выражения:

где α – параметр обучения; а 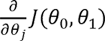является производной функции стоимости по θ_j. Знак := означает присваивание, в отличие от знака равенства (=), применяемого в алгебраических выражениях.

При этом шаги алгоритма выполняются так, что вначале происходит одновременное изменение обоих параметров на основании выражения 2.2 и только затем использование их для расчета новых значений функции стоимости. Другими словами, алгоритмическая последовательность одного из шагов цикла для случая двух параметров, выраженная на псевдокоде, будет следующей:

Отметим, что выражение функции гипотезы можно преобразовать следующим образом:

и записать в виде:

с учетом того, что x₀ = 1. Последнее выражение позволяет вычислять функцию гипотезы путем матричного умножения матрицы X, первая колонка которой всегда состоит из единиц, на вектор θ.

С учетом дифференцирования выражения 1.3 и 1.4 можно переписать в виде:

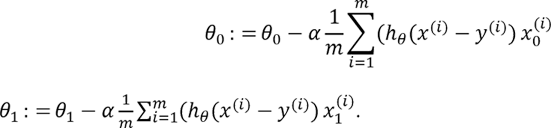
В зависимости от параметра обучения α алгоритм может достигать минимума (сходиться) или же при слишком большом α не сходиться.

Наиболее простой в реализации, но не оптимальный по времени выполнения пакетный алгоритм градиентного спуска (Batch Gradient Descent) использует все обучающие примеры на каждом шаге алгоритма. Вместо алгоритма градиентного спуска для нахождения параметров θ_j можно использовать матричное выражение:

где θ – вектор параметров; (X^TX)^-1 – обратная матрица X^TX; X^T – транспонированная матрица X.

Преимуществом матричных операций является то, что нет необходимости подбирать параметр α и выполнять несколько итераций алгоритма. Недостаток связан с необходимостью получения обратной матрицы, сложность вычисления которой пропорциональна O(n³), а также c невозможностью получения обратной матрицы в некоторых случаях.

Рассмотрим пример.

Решим гипотетическую задачу нахождения параметров линейной регрессии методом градиентного спуска. Во-первых, подключим необходимые библиотеки:

%matplotlib inline

import matplotlib.pyplot as plt

import numpy as np

import time

Отметим, что библиотека time позволит нам рассчитать время выполнения программы. Ее применение будет понятно из нижеследующего кода. Сформируем обучающее множество, состоящее из 30 примеров:

xr=np.matrix(np.linspace(0,10,30))

x=xr.T

#значения функции зададим в виде следующего выражения

y=np.power(x,2)+1

#Построим график (рисунок) командами

plt.figure(figsize=(9,9))

plt.plot(x,y,'.')

Рисунок 2.2. График функции y=x₂+1

В нашем случае мы задали фиксированное множество примеров (m = 30), однако в дальнейшем мы можем его изменить. Для тогo чтобы программа воспринимала любое множество примеров, определим его, используя метод size:

m=x.size

#сформируем первую колонку матрицы X, состоящую из единиц

on=np.ones([m,1])

#и сформируем матрицу X, объединив колонки

X=np.concatenate((on,x),axis=1)

Это матрица, в первой колонке которой стоят единицы, а во второй – значения x⁽¹⁾, x⁽²⁾,…, x^(m). Затем зададим абсолютно произвольно начальные значения коэффициентов регрессии:

theta=np.matrix('0.1;1.3')

#и рассчитаем значения функции гипотезы

h=np.dot(X,theta)

#дополним предыдущий график регрессионной прямой

plt.plot(x,h)

Получим график вида:

Рисунок 2.3. Начальное положение прямой регрессии

На графике видно, что прямая функция гипотезы далека от идеальной. Применим алгоритм градиентного спуска для нахождения оптимальных значений параметров регрессионной прямой (функции гипотезы):

t0=time.time()

alpha=0.05

iterations=500

for i in range(iterations):

theta=theta-alpha*(1/m)*np.sum(np.multiply((h-y),x))

h=np.dot(X,theta)

t1=time.time()

#Построим графики

plt.figure(figsize=(9,9))

plt.plot(x,y,'.')

plt.plot(x,h,label='regressionByIteration')

leg=plt.legend(loc='upper right',shadow=True,fontsize='x-small')

leg.get_frame().set_facecolor('#0055DD')

leg.get_frame().set_facecolor('#eeeeee')

leg.get_frame().set_alpha(0.5)

plt.show()

Получим следующий график регрессионной прямой:

Рисунок 2.4. Результат выполнения алгоритма градиентного спуска

#рассчитаем среднеквадратическую ошибку

mse=np.sum(np.power((h-y),2))/m

print('regressionByIteration mse= ', mse)

#и распечатаем длительность выполнения цикла градиентного спуска

print('regressionByIterations takes ',(t1-t0))

Получим примерно следующий вывод:

regressionByIterations mse = 63.270782365456206

regressionByIterations takes 0.027503490447998047

В качестве небольшого дополнения рассчитаем показатели точности регрессии с применением библиотеки метрик sklearn.

from sklearn.metrics import mean_squared_error, r2_score

y_predict = h

y_test=y

print("Mean squared error: {:.2f}".format(mean_squared_error(y_test,y_predict)))

print("r2_score: {:.2f}".format(r2_score(y_test, y_predict)))

Получим следующие результаты:

Mean squared error: 63.27

r2_score: 0.93

Подробнее о метриках точности классификации и регрессии см. в разделе «3. Оценка качества методов ML».

2.3. Полиномиальная регрессия

В отличие от линейной регрессии, полиномиальная регрессия оперирует нелинейной функцией гипотезы вида , что позволяет строить экстраполирующие кривые (гиперповерхности) сложной формы. Однако с увеличением числа параметров существенно возрастает вычислительная сложность алгоритма. Кроме этого, существует опасность «переобучения», когда форма кривой или гиперповерхности становится слишком сложной, практически полностью подстроившись под обучающее множество, но дает большую ошибку на тестовом множестве. Это свидетельствует о том, что алгоритм потерял способность к обобщению и предсказанию. В случае переобучения, когда классификатор теряет способность к обобщению, применяют регуляризацию, снижающую влияние величин высокого порядка:

Увеличение коэффициента λ приводит к повышению степени обобщения алгоритма. В пределе при очень большом значении λ функция гипотезы превращается в прямую или гиперплоскость. Практически это означает, что алгоритм будет вести себя слишком линейно, что также неоптимально. Задача исследователя – подобрать коэффициент регуляризации таким образом, чтобы алгоритм был не слишком линеен и в то же время обладал достаточной способностью к обобщению.

Вычисление параметров регрессии методом градиентного спуска выполняется так же, как и ранее, за исключением небольшого дополнения в виде регуляризационного коэффициента, так что для j-го параметра на каждом шаге цикла вычисляется значение:

Рассмотрим пример.

В качестве исходных данных синтезируем набор данных в соответствии с выражением:

Добавив некоторый случайный коэффициент с помощью np.array([np.random.rand(x.size)]).T/50, получим примерно следующее (рисунок 2.5):

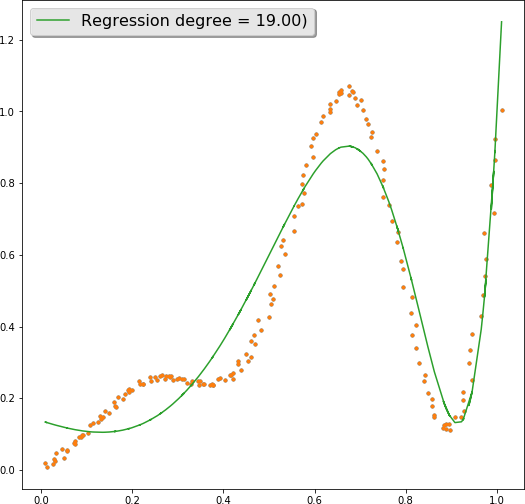
Рисунок 2.5. Исходные данные и результаты выполнения алгоритма полиномиальной регрессии

Введем переменную degree, означающую коэффициент регрессии. Например, при degree = 1 получим обычную линейную регрессию (r2_score = 0.27). Увеличивая степень регрессии, можем добится значительно лучших результатов. Например, при degree = 19 r2_score = 0.90. Использование коэффициента регуляризации lambda_reg позволяет «сглаживать» регрессионную кривую. Фрагмент программы, обеспечивающей расчет параметров полиномиальной регрессии, приведен ниже:

xr=np.array([np.linspace(0,1,180)])

x=xr.T

print(x.size)

y=f(x)

(x,y)=plusRandomValues(x,y) #добавление случайных величин

plt.figure(figsize=(9,9))

plt.plot(x,y,'.')

m=x.size

degree=19 #коэффициент регрессии

lambda_reg=0.00001

on=np.ones([m,1])

X=on

#расчет степеней свободной переменной в соответствии со степенью регрессии degree

for i in range(degree):

    xx=np.power(x, i+1)

    X=np.concatenate((X,xx),axis=1)

theta=np.array([np.random.rand(degree+1)])

h=np.dot(X,theta.T)

t0=time.time()

alpha=0.5

iterations=100000

for i in range(iterations):

    theta=theta-alpha*(1/m)*np.dot((h-y).T,X) -(lambda_reg/m)*theta

    h=np.dot(X,theta.T)

t1=time.time()

plt.plot(x,y,'.')

plt.plot(x,h, label='Regression degree = {:0.2f})'.format(degree))

leg=plt.legend(loc='upper left',shadow=True,fontsize=16)

leg.get_frame().set_facecolor('#0055DD')

leg.get_frame().set_facecolor('#')

leg.get_frame().set_alpha(0.9)

plt.show()

2.4. Классификаторы. Логистическая регрессия

Несмотря на присутствующее в названии данного метода слово «регрессия», цель данного алгоритма не восстановление значений или предсказание. Алгоритм применяется в случае, если необходимо решить задачу классификации. В случае логистической регрессии речь идет о задаче бинарной классификации, то есть отнесении объектов к классу «негативных» или «позитивных», вследствие чего набор обучающих примеров построен таким образом, что y ∈ {0,1}.

В этом случае от функции гипотезы требуется выполнение условия 0 ≤h_θ(x) ≤1, что достигается применением сигмоидальной (логистической) функции:

Где θ – вектор параметров.

Можно записать также

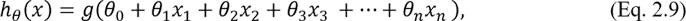
где n – число параметров (свойств или признаков) объектов; g(z) – сигмоидальная или логистическая функция.

В сокращенном виде h_θ(x) = g(θ^Tx).

Отметим, что сигмоидальная функция широко применяется и в нейронных сетях в качестве активационной функции нейронов, поскольку является непрерывно дифференцируемой и тем самым гарантирует сходимость алгоритмов обучения нейронной сети. Примерный вид сигмоиды показан в разделе «Активационные функции».

Функция h_θ(x) может рассматриваться как вероятность того, что объект является «позитивным» (h_θ(x)≥0.5) или «негативным» (h_θ(x)<0.5). В сложных случаях, требующих нелинейной границы разделения, например, в виде окружности (рисунок 2.6), необходимо добавить дополнительные параметры, например, квадратные степени исходных параметров:

или их произведения и т.п.

Рисунок 2.6. Объекты, для которых необходима нелинейная граница разделения

Подбор параметров θ после выбора функции гипотезы выполняется так, чтобы минимизировать функцию стоимости вида:

Из двух частей функции стоимости, объединенных знаком +, вычисляется фактически только одна, так как в задаче классификации y может принимать только два значения: 1 и 0.

То есть в случае, если y = 0, стоимость для i-го примера принимает вид:

Таким образом, при минимальном значении функции стоимости в обоих случаях достигается максимизация вероятности принадлежности объекта к положительному классу для «положительных» объектов и минимизация вероятности для «отрицательных» объектов. По-другому логистический классификатор называется классификатором максимизации энтропии (maximum-entropy classification – MaxEnt).

Как и в случае с линейной регрессией, минимизация функции стоимости достигается с помощью алгоритма градиентного спуска (gradient descent), но также применяются Conjugate gradient [^[36]], BFGS, L-BFGS или lbfgs [^[37]].

Логистический классификатор может быть применен и в отношении нескольких классов. В этом случае для каждого класса классификатор настраивается отдельно. Класс, к которому принадлежит новый объект, вычисляется расчетом значений всех функций гипотез и выбором из них максимального значения m_iaxh_θ⁽ⁱ⁾(x), где i – номер класса. Другими словами, объект принадлежит к тому классу, функция гипотезы которого максимальна.

Как и в случае с линейной регрессией, для увеличения обобщающей способности алгоритма применяют регуляризацию (последнее слагаемое в нижеследующей формуле), которая позволяет уменьшить влияние величин высокого порядка:

Интересно, что производная функции стоимости логистической регрессии ровно такая же, как и производная функции стоимости линейной регрессии (вывод см., например, в [^[38]]). Следовательно, алгоритм градиентного спуска будет работать так же, как и для линейной регрессии (формула 1.5), с тем отличием, что значение функции гипотезы будет вычисляться по формуле 2.8.

Пример. Построим линейный классификатор на основе логистической регрессии. Вначале сгенерируем набор данных и разделим его на тренировочное и тестовое множества:

from sklearn.datasets import make_moons, make_circles, make_classification

from sklearn.model_selection import train_test_split

dataset = make_circles(noise=0.2, factor=0.5, random_state=1)

X_D2, y_D2 = dataset

plt.figure(figsize=(9,9))

plt.scatter(X_D2[:,0],X_D2[:,1],c=y_D2,marker='o',

      s=50,cmap=ListedColormap(['#FF0000','#00FF00']))

X_train, X_test, y_train, y_test = train_test_split(X_D2, y_D2, test_size=.4, random_state=42)

В результате получим распределение данных, показанное на рисунке 1.3.

Вызовем необходимые библиотеки и методы:

import matplotlib.pyplot as plt

import numpy as np

from sklearn.metrics import confusion_matrix, classification_report

from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score

Последние две строки необходимы для оценки точности работы классификатора (см. раздел «Оценка качества методов ML»).

Разработаем логистическую функцию logisticFunction(X,theta) и функцию, обеспечивающую оценку объекта на основе предсказанного значения гипотезы, – logRegPredictMatrix(h,threshold). Как показано выше, функция гипотезы принимает значение от 0 до 1. Для того чтобы получить оценку принадлежности объекта к классу (1 – «положительный», 0 – «отрицательный»), необходимо для каждого значения гипотезы вычислить номер класса («предсказать») по правилу predicted = 0 If h <threshold и predicted = 1 If h >= threshold. Обычное значение порога threshold=0.5.

Функция, вычисляющая значения коэффициентов логистической регрессии первого порядка:

def logisticRegressionByNumpy(X,y):

   m=y.size

   X=np.concatenate((np.ones([m,1]),X), axis=1)

   theta=np.array(np.random.rand(X.shape[1]))

   h=logisticFunction(X,theta)

   alpha=0.05

   iterations=1500

   lambda_reg=0.01

   for i in range(iterations):

   theta=theta – alpha*(1/m) *np.dot(X.T,(h-y))-(lambda_reg/m)*theta

      h=logisticFunction(X,theta)

   return theta,h

Вызов функции и вывод показателей качества можно выполнить:

theta,h=logisticRegressionByNumpy(X_train,y_train)

predicted_train=logRegPredictMatrix(h,threshold=0.50)

matrix_train = confusion_matrix(y_train, predicted_train)#,labels)

print('Logistic regression')

print('Results on train set')

print('Accuracy on train set: {:.2f}'.format(accuracy_score(y_train, predicted_train)))

print('Conf. matrix on the train \n', matrix_train)

print('Classification report at train set\n',

    classification_report(y_train, predicted_train, target_names = ['not 1', '1']))

В результате получим на тренировочном множестве значение accuracy = 0.57, а на тестовом 0.4. Другими словами, точность предсказания нашей функции хуже, чем при случайном выборе классов! Подобный результат вполне предсказуем, поскольку мы попытались использовать прямую там, где требуется как минимум окружность.

Исправить положение можно, используя регрессию второго порядка в соответствии с выражением (2.10). В предыдущей функции достаточно изменить одного оператора:

X=np.concatenate((np.ones([m,1]),X,X**2), axis=1)

После этого мы получим значение accuracy на тренировочном и тестовом множествах, равное 0.9, что вполне приемлемо для нашей задачи.

Необходимость подбора значимых параметров и формирования новых параметров является одним из недостатков логистической регрессии.

Вторым недостатком данного метода является то, что он предназначен для решения задач бинарной классификации.

Третья проблема, вытекающая из структурных свойств графического представления логистической регрессии, заключается в том, что она не способна напрямую решать некоторые классические логические задачи.

Для преодоления этих недостатков используются искусственные нейронные сети. Однослойные нейронные сети способны решать задачу мультиклассовой классификации, а многослойные нейронные сети успешно преодолевают все три ограничения.

Примечание. Программный код примера MLF_logReg_Python_numpy_002.ipynb, описанного в этом разделе, можно получить по ссылке

https://www.dropbox.com/s/vlp91rtezr5cj5z/MLF_logReg_Python_numpy_002.ipynb?dl=0