
Надежда Лаврова
Все аспекты деятельности испытательной лаборатории. Практическое пособие
4.3. Способы и методы внутрилабораторного контроля качества измерений
Можно выделить следующие основные способы ВЛК качества измерений:
– контроль стабильности измерений с помощью контрольных карт;
– проверку приемлемости результатов измерений;
– точечную оценку метрологических характеристик измерений за тот или иной период.
Основным инструментом ВЛК является контроль стабильности измерений с помощью контрольных карт. Контроль стабильности основан на анализе результатов регулярных измерений какого-либо стабильного показателя, характеризующего результаты измерений, причем измерения рекомендуется выполнять в каждой серии. Лучше всего, когда таким показателем является собственно измеряемый показатель – в химическом анализе это концентрация определяемого вещества (веществ) в контрольном материале. Под контрольным материалом мы понимаем однородный и стабильный (хотя и не обязательно аттестованном) образец, близкий по свойствам к исследуемым образцам. Возможен также контроль стабильности при отсутствии контрольного материала (что хуже). При других измерениях для контроля стабильности используется любой объект с неизменными свойствами.
Помимо контроля по определяемому показателю в КХА могут использоваться и другие: аналитический сигнал образца сравнения, используемого при градуировке; величины, по которым контролируется качество отдельных стадий анализа (например, масса или объем отобранных на одной из стадий химического анализа аликвот) и т. д. Нужно лишь, чтобы эти характеристики были стабильными в подконтрольном состоянии и отражали бы качество измерений.
Проверка приемлемости результатов измерений может выполняться в случаях, когда для одного рутинного образца выполняется более одного измерения. В этом случае, для каждого рутинного образца можно найти размах (разницу между максимальным и минимальным результатами измерений) и сравнить ее с максимально допустимой. В случае превышения, для получения окончательно приводимого результата, в большинстве случаев выполняются дополнительные измерения и рассчитывается медиана всех результатов. С точки зрения контроля, основной процедурой является процедура оценки размаха, в ходе которой, фактически, контролируется дисперсия. Используются разные критерии, но в любом случае, значительное число проб, для которых размах превысил допустимый размер, свидетельствует о достоверном увеличении внутрисерийного разброса результатов.
Точечная оценка метрологических характеристик измерений за тот или иной период выполняется по результатам различных измерений, как выполненных для контрольных, так и для рутинных материалов (образцов).
В качестве внутрилабораторного контроля целесообразно использовать один из следующих методов с указанными критериями оценки (анализом ВЛК):
– проведение сличительных измерений (испытаний), разными специалистами, или приборами (Контроль прецизионности в условиях воспроизводимости). Критерий оценки- диапазоны измеренных значений с учётом неопределённости измерения должны перекрывать друг друга. Следует рассматривать как наиболее предпочтительную процедуру;
– дублирование проводимых измерений (испытаний) с использованием разных методов/СИ (производится по устному или письменному распоряжению руководства для подтверждения полученных ранее результатов). Критерий оценки- диапазоны измеренных значений с учётом неопределённости измерения должны перекрывать друг друга;
– повторные исследования сохраняемых объектов. Критерий оценки- диапазоны измеренных значений с учётом неопределённости измерения должны перекрывать друг друга. Пример – шифрованная проба для спектрометра, образец для проведения испытаний по определению свинцового эквивалента;
– проведение процедур, обеспечивающих контроль достоверности текущих измерений, в том числе с использованием стандартных образцов. Критерий оценки – измеренное значение не должно превышать диапазона допустимых значений, принятый для стандартных образцов (методики измерений, или погрешности прибора). Пример – контрольный источник для спектрометра;
– проверка проведения измерений в строгом соответствии с требованиями применяемой методики испытания, под надзором Руководителя испытательной лаборатории или более опытного сотрудника. Критерием оценки является должный уровень владения применяемой методикой испытания;
– измерение (испытание) проб объектов (с нулевым содержанием/ величиной). Критерий оценки – измеренное значение должно быть не больше нижнего предела диапазона измерений (испытаний);
– проведение «если это возможно в условиях испытательной лаборатории» отдельных пунктов по поверке прибора. Например, проверка воспроизводимости показаний прибора, проверка долговременной стабильности. Критерием оценки является соответствие выполняемых пунктов:
– контроль фоновых показаний. Измерения, подтверждающие, что погрешность нуля не превышает установленных пределов;
– участие в межлабораторных сравнительных испытаниях и программах проверки квалификации, межлабораторных экспериментов. Оценку в данном случае производит независимая организация.
В некоторых случаях есть возможность не ограничиваться данными процедурами. В качестве дополнительных мер по контролю качества могут быть использованы внутренние алгоритмы приборов, позволяющие производить самодиагностику. Критерий оценки должен быть прописан в инструкции по эксплуатации. Проверка прибора осуществляется специалистом, если результаты измерений в ежедневной практике вызывают сомнения.
Ведение ВЛК (расчет и уточнение параметров контрольных карт и их вычерчивание на бумаге, отслеживание появления тревожных и контрольных признаков, выполнение других необходимых расчетов) вручную всегда было неудобным делом, а, с появлением усложненных его вариантов, рекомендованных в ГОСТ Р ИСО 5725-6-2002 стало совсем малореальным.
Лаборатории, систематически выполняющие определение большого числа показателей, практически никогда не успевают все это делать, в лучшем случае задним числом вычерчивая контрольные карты к очередной аккредитации или инспекционному контролю.
Проблема нашла свое решение с появлением компьютерных программ, позволяющих полностью или частично автоматизировать внутрилабораторный контроль, проводя расчеты с помощью компьютера и отказавшись от ведения контрольных карт в бумажной форме.
Существует много компьютерных программ для ВЛК. Главным образом это специализированные программы, являющиеся неотъемлемой частью того или иного аналитического прибора. Конечно, они удобны, но очень дороги (так, стоимость программы для контроля качества к атомно-абсорбционным спектрофотометрам фирмы «Perkin-Elmer» достигает $5000) и узко специализированы. Кроме того, они не всегда соответствуют существующим нормативным документам.
Другим вариантом решения является использование программ для ВЛК общего назначения, данные в которые вводятся с клавиатуры компьютера (что не исключает, конечно, и их подключения непосредственно к приборам на заказ). В России получила распространение программа «QControl», работающая под Windows, рекомендованная к использованию Госстандартом России и распространяемая несколькими организациями (например, фирмой «Амперсенд» и ассоциацией «Аналитика»). Эта программа в настоящее время полностью соответствует ГОСТ Р ИСО 5725—2002.
4.4. Элементы системы внутрилабораторного контроля
Обеспечение качества при реализации ВЛК в испытательной лаборатории является важной и актуальной задачей для каждой лаборатории, заявляющей о своей компетентности.
Важнейшими элементами в системе ВЛК являются:
– оперативный контроль процедуры определений (основан на оценке погрешности результатов испытаний при осуществлении определенного вида процедуры контроля);
– контроль стабильности результатов определений (основан на контроле стабильности таких показателей, как среднеквадратическое отклонение внутрилабораторной прецизионности, среднеквадратическое отклонение повторяемости, значение характеристики погрешности).
Выделяют следующие формы контроля стабильности результатов испытаний:
1. Контроль за стабильностью результатов испытаний в конкретной лаборатории с применением контрольных карт путем поддержания на заданном уровне:
– характеристик погрешности результатов испытаний;
– показателей внутрилабораторной прецизионности, в том числе значений повторяемости результатов параллельных испытаний;
2. Систематическая проверка подконтрольности процедур осуществления измерений (испытаний, анализа);
3. Выборочный статистический контроль показателей внутрилабораторной прецизионности и погрешности результатов испытаний, выполненных в течение заданного промежутка времени. Этот вид контроля рекомендуется осуществлять по альтернативному признаку.
Анализ информации, полученной при контроле стабильности результатов, позволяет осуществить оценку внутрилабораторной прецизионности, погрешности результатов испытаний, проводить их сопоставление с установленными значениями, а также реализовывать контроль систематической погрешности данной лаборатории.
С целью обеспечения качества при реализации внутрилабораторного контроля ежегодно составляется график построения и проверки градуировочных характеристик, а также предусматривается проведение контроля методом добавок, разведения, использование образца для контроля, ведется контроль погрешности на основе применения контрольных проб с использованием контрольных карт.
Контроль за стабильностью результатов испытаний основан на оценке величины систематической и случайной погрешности. Систематическая погрешность всегда сдвигает результаты в одну и ту же сторону, случайная же погрешность меняется по значению и зависит от многих случайных изменений (например, внешних условий). Отследить случайную ошибку гораздо сложнее, чем систематическую, также, как и выявить причину ее возникновения. Случайные погрешности являются неустранимыми, и только тщательно налаженная стандартизация всех этапов анализа, строгое соблюдение условий исследования и учет многочисленных факторов, влияющих на анализ, позволяют свести случайную погрешность измерения к минимуму. К случайной погрешности, как правило, относится и промах (грубая погрешность измерений), характеризующийся тем, что погрешность результата отдельного измерения, входящего в ряд измерений, для данных условий резко отличается от остальных результатов этого ряда.
Грубые ошибки – это ошибки одиночного значения, когда результаты исследований выходят за пределы области определяемого компонента. Эти ошибки могут быть субъективными, которые зависят от квалификации специалиста, недостаточной тщательности его работы.
Рис. 4.4. Сочетание случайных и систематических погрешностей
Возникают ошибки обычно из-за недосмотра: ошибка при регистрации результата, неправильное дозирование пробы, перепутан реактив, неподходящий фильтр при фотометрии, ошибка в разведении, подсчете, небрежность в проведении метода исследования и т. д. Грубые ошибки могут быть и объективными, зависящими от чистоты лабораторной посуды, реактивов, состояния приборов и др. Грубая погрешность существенно превышает ожидаемую погрешность и, как правило, видна невооруженным глазом. Такие результаты отбрасываются, и производится повторный анализ пробы.
Сочетание случайных и систематических погрешностей показано на рис. 4.4.
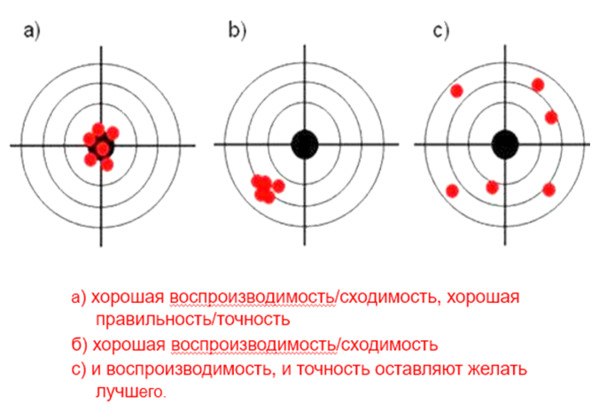
Воспроизводимость и правильность являются основными показателями качества результата лабораторного теста, потому что они характеризуют полную ожидаемую ошибку результата лабораторного измерения, другими словами насколько измеряемое содержание в пробе исследуемого параметра будет отличаться от его «истинного» значения. Воспроизводимость – качество измерений, отражающее близость друг к другу результатов измерений, выполняемых в различных условиях (т. е. степень совпадения результатов повторных измерений одной и той же пробы). Воспроизводимость измерений характеризует наличие случайных погрешностей. Случайная погрешность – это составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины.
Правильность – качество измерений, отражающее близость к нулю систематических погрешностей в результатах. Правильность измерений характеризует наличие систематических погрешностей. Систематическая погрешность – это составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Систематическая погрешность определяется близостью среднего результата повторных измерений контрольного материала (X̅.) к аттестованному значению измеряемой величины (АЗ). Систематическая погрешность может быть выражена в абсолютных и/или относительных величинах.
Относительная систематическая погрешность В (относительное смещение):
В = (X̅ – АЗ) 100% / АЗ (4.1)
В ГОСТ Р ИСО 5725—2002 вводится общий термин «прецизионность» для всех видов случайных погрешностей. Прецизионность – степень близости (или степень разброса) результатов для серии измерений, выполненных по данной методике на различных пробах одного и того же однородного образца. Прецизионность может рассматриваться на трех уровнях: сходимость, внутрилабораторная прецизионность и воспроизводимость.
Сходимость результатов измерений – отсутствие существенных различий между результатами измерений, выполняемых в одинаковых условиях (контроль сходимости и воспроизводимости результатов исследований может осуществляться с помощью контрольного материала с неисследованным содержанием).
Термины «повторяемость» и «сходимость» становятся синонимами («повторяемость (сходимость)») и относятся к измерениям, выполняемым в течение краткого промежутка времени, одним исполнителем, на одном и тем же оборудовании, с использованием одних и тех же реактивов и т. д. («в условиях повторяемости»). Мерой повторяемости (сходимости) является дисперсия повторяемости S2. Другими словами, это минимально возможная для методики измерений систематическая погрешность. Дисперсия дает характеристику разброса данных вокруг центра.
S2 = СУММА (Хi – X̅) 2 / (n – 1) (4.2)
где S2 – выборочная дисперсия;
n – количество измерений;
X – отдельные значения;
X̅— среднее арифметическое по выборке.
Дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности. Разница между отдельным значением и средней отражает меру отклонения. В квадрат возводится для того, чтобы все отклонения стали исключительно положительными числами и, чтобы избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Затем, имея квадраты отклонений, мы просто рассчитываем среднюю арифметическую. Однако в чистом виде, как, например, средняя арифметическая, или индекс, дисперсия не используется. Это скорее вспомогательный и промежуточный показатель, который необходим для других видов статистического анализа. У нее нет даже единицы измерения. Чтобы использовать дисперсию в более приземленных целей, из нее извлекают квадратный корень, получается среднеквадратичное отклонение (СКО или S), иногда его называют стандартное отклонение.
Рис. 4.5. Пример выборки с коэффициентом вариации 45%
Среднеквадратичное отклонение вычисляется по формуле:
S = √ (СУММА (Хi – X̅) 2 / (n – 1)) (4.3)
где √ – корень квадратнный из суммы;
Х i – результат i-го измерения из n выполненных;
n – количество измерений;
X̅ – среднее арифметическое значение.
Среднее арифметическое значение вычисляется по формуле:
X̅ = СУММА Х i / n (4.4)
где Х i – сумма результатов измерений с 1-го до n-ного;
n – количество измерений.
Математически, случайная погрешность может быть выражена не только величиной среднеквадратичного отклонения, но и коэффициентом вариации (CV). Среднее квадратичное отклонение дает абсолютную оценку меры разброса. Поэтому, чтобы понять, насколько разброс велик относительно самих значений (т.е. независимо от их масштаба), требуется относительный показатель – коэффициент вариации.
Коэффициент вариации – это стандартное отклонение, выраженное в процентах от среднего значения.
CV = S 100% / X̅ (4.5)
где X̅ – среднее арифметическое значение;
S – среднеквадратичное отклонение.

Рис. 4.6. Пример выборки с коэффициентом вариации 24%
Этот показатель вариации прекрасен тем, что и меру рассеяния учитывает, и единиц измерения не имеет, то есть совершенно не связан с масштабом анализируемых данных.
Исходя из этого факта, коэффициенты вариации можно сравнивать между собой и тем самым сопоставлять относительную меру рассеяния данных, независимо от их масштаба.
В статистике принято считать, что, если значение коэффициента вариации менее 30%, то совокупность данных является однородной, если более 30%, то – неоднородной. Что это означает?
Рассмотрим пример выборки с коэффициентом вариации 45% (рис. 4.5).
На графике видно, что диапазон разброса до плюс/минус 80, совокупность результатов анализа неоднородна.
Рассмотрим пример выборки с коэффициентом вариации 24% (рис.4.6).

При сравнении графиков видны отличия однородных данных от неоднородных. На втором графике – данные однородны со значением коэффициента вариации 24%, на первом – неоднородны со значением вариации 45%. Чем более однородны данные, тем ближе они находятся к среднему значению. Чем менее однородны, тем больше рассеяны и находятся дальше друг от друга и от своей средней. Если показатель вариации составляет примерно 30% и меньше, то статистическая совокупность считается однородной. Это означает, что большинство показателей находится недалеко от средней величины, и найденное значение хорошо характеризует центральную тенденцию совокупности. Если показатель вариации составляет существенно больше 30%, то выборка неоднородна, то есть, значительное количество показателей находится далеко от, и выборочная средняя плохо характеризует правильный результат.
Правильность измерений – отсутствие систематических погрешностей в результатах (для контроля правильности используется только материал с исследованным содержанием компонентов).
Повторяемость (сходимость) результатов испытаний. Характеристика результатов испытаний, определяемая близостью результатов испытаний одного и того же объекта по одной и той же методике в соответствии с требованиями одного и того же нормативного документа в одной и той же лаборатории одним и тем же оператором с использованием одного и того же экземпляра оборудования в течение короткого промежутка времени (ГОСТ Р 51672) (внутрилабораторный контроль).
Норматив (предел) повторяемости (сходимости) -предельно допускаемое абсолютное расхождение между двумя результатами испытаний, полученными в условиях повторяемости (сходимости) для доверительной вероятности 0,95.
В соответствии с ГОСТ Р ИСО 5725—1, воспроизводимость результатов испытаний определяется как характеристика результатов испытаний, определяемая близостью результатов испытаний одного и того же объекта по единым методикам в соответствии с требованиями одного и того же нормативного документа с применением различных экземпляров оборудования разными операторами в разное время. Такие условия обеспечиваются при проведении испытаний в разных лабораториях (межлабораторный контроль).
Термин «воспроизводимость» связан с межлабораторным разбросом результатов измерений. Таким образом, в применении к внутрилабораторному контролю термин «воспроизводимость» вообще использоваться не должен: для отдельно взятой лаборатории соответствующий эффект уже не является случайным; он вырождается в систематическую погрешность этой лаборатории. Однако, при обычной в лабораторной практике ситуации, когда разные группы проб исследуются на одном и том же оборудовании, одним и тем же лаборантом, но в разное время и с использованием разной калибровки, может возникнуть случайная погрешность, которая выявляется путем оценки вопроизводимости. При записи результатов рекомендуется указывать, какие именно факторы изменяются. Всего рассматриваются четыре фактора (время T, калибровка C, оператор O, оборудование E).
Норматив (предел) воспроизводимости – предельно допускаемое абсолютное расхождение между двумя результатами испытаний, полученными в условиях воспроизводимости для доверительной вероятности 0,95.
Запись результата измерений должна сопровождаться указанием его надежности P. Под надежностью или доверительной вероятностью понимают вероятность того, что истинное значение измеряемой величины заключено в интервале, указанном записью. Сам этот интервал называется доверительным интервалом. Например, измеряя длину некоторого отрезка, окончательный результат записать в виде:
L = (8,34 ± 0.02) мм, (P = 0.95)
Это означает, что 95 шансов из 100 шансов за то, что истинное значение длины отрезка заключается в интервале от 8,32 до 8,36 мм. Например, ГОСТы на методы испытаний требуют, чтобы запись результата анализа была сделана, как результата среднеарифметического показателя двух результатов измерений, расхождение между которыми не должно превышать 0,5% при Р=0,95%.
Применительно к нормальному закону распределения значения коэффициентов охвата были впервые рассчитаны английским математиком У. Госсетом, подписывавшим свои труды псевдонимом Стьюдент, и потому называются коэффициентами Стьюдента. Коэффициенты Стьюдента имеют специальное обозначение t. Таким образом, в предположении подчинения случайной величины x нормальному закону распределения формула для расчета ее доверительного интервала принимает вид x ± t (P, f) s (x). Коэффициенты Стьюдента зависят от двух параметров: доверительной вероятности P и числа степеней свободы f, соответствующего стандартному отклонению s (x). Причина зависимости t от P очевидна: чем выше доверительная вероятность, тем шире должен быть доверительный интервал с тем, чтобы можно было гарантировать попадание в него значения величины x. Поэтому с ростом P значения t возрастают. Зависимость t от f объясняется следующим образом. Поскольку s (x) – величина случайная, то в силу случайных причин ее значение может оказаться заниженным. В этом случае и доверительный интервал окажется более узким, и попадание в него значения величины x уже не может быть гарантировано с заданной доверительной вероятностью. Чтобы «подстраховаться» от подобных неприятностей, следует расширить доверительный интервал, увеличить значение t, причем тем больше, чем менее надежно известно значение s, т.е. чем меньше число его степеней свободы. Поэтому с уменьшением f величины t возрастают. Коэффициенты Стьюдента для различных значений P и f приведены в табл. 4.1.
При расчете доверительного интервала встает вопрос о выборе доверительной вероятности P. При слишком малых значениях P выводы становятся недостаточно надежными. Слишком большие (близкие к 1) значения брать тоже нецелесообразно, так как в этом случае доверительные интервалы оказываются слишком широкими, малоинформативными.
Таблица 4.1.
Коэффициенты Стьюдента
Для большинства химико-аналитических задач оптимальным значением P является 0,95.
Пример расчёта доверительного интервала приведён ниже.








