Людвиг Витгенштейн
Логико-философский трактат. Философские исследования
Суждение есть описание позиции.
Описание объекта описывает последний по его внешним свойствам, а суждение описывает реальность по ее внутренним свойствам.
Суждение создает мир при помощи логических строительных лесов, и из суждения, если оно истинно, можно заключить, насколько все логично. Из ложного суждения возможно делать выводы.
4.024. Понять суждение значит узнать, что имеет место быть, если суждение истинно.
(И потому возможно понять суждение, не зная, истинно ли оно.)
Суждение понятно всякому, кто понимает его составные части.
4.025. При переводе с одного языка на другой мы вовсе не переводим суждение на одном языке в суждение на другом, но переводим составные части суждений.
(А словарь переводит не только имена существительные, но и глаголы, прилагательные, наречия и т. д. и трактует все части речи сходным образом.)
4.026. Значения простых знаков (слов) следует объяснять, чтобы мы их поняли.
Но чтобы поняли нас, требуются суждения.
4.027. Суть суждения заключается в том, что оно должно передавать новый смысл.
4.03. Суждение должно использовать существующие выражения для передачи нового смысла.
Суждение передает ситуацию и потому должно быть непосредственно связано с ситуацией.
Эта связь представляет собой не что иное, как логическую картину.
Суждение сообщает что-либо лишь тогда, когда это что-либо присутствует на картине.
4.031. В суждении ситуация как таковая создается опытным путем.
Вместо фразы «Это суждение имеет такой-то и такой-то смысл» мы можем просто сказать: «Это суждение представляет такую-то ситуацию».
4.0311. Одно имя соответствует одному предмету (явлению), другое – другому, и они сочетаются друг с другом. В этом отношении группа – подобно живой картине – отображает позицию.
4.0312. Возможность суждений основана на том принципе, что объекты представляются знаками.
Моя основная идея такова: «логические константы» не являются отображениями; в логике фактов нет отображений.
4.032. Лишь если суждение логически артикулировано, оно может быть картиной ситуации.
(Даже суждение «Амбуло» является составным, поскольку различные окончания его основы создают различные смыслы, как и окончание с иной основой.)
4.04. В суждении должно быть столько же отдельных частей, сколько в ситуации, которую оно отображает.
Суждение и ситуация должны обладать одинаковым логическим (математическим) многообразием. (Ср. «Механику» Герца с ее динамическими моделями [8].)
4.041. Это математическое многообразие, конечно, само не может быть объектом описания. При описании невозможно выйти за его пределы.
4.0411. Если, к примеру, то, что выражается как «(x) × fx», записать, предпослав «fx» некий индекс – допустим, «Alg × fx», – запись будет некорректной, поскольку мы не знаем, что именно обобщается. Уточнение при помощи индекса «a» – допустим, «f(xa)» – тоже было бы некорректным: мы не знаем размерности знака общности.
Если ввести некий знак на аргументные места – допустим, так:
«(А, А) × F (А, А)», —
попытка не будет удачной, поскольку мы не в состоянии установить тождество переменных. И т. д.
Все эти формы записи некорректны, поскольку им недостает необходимого математического многообразия.
4.0412. По той же причине идеалистическая тяга к «пространственным очкам» для объяснения пространственных отношений некорректна, поскольку она не может объяснить многообразие этих отношений.
4.05. Реальность сравнивается с суждениями.
4.06. Суждение может быть истинным или ложным только в силу того, что оно является картиной реальности.
4.061. Нельзя упустить то обстоятельство, что суждение обладает смыслом, не зависящим от фактов; иначе легко заключить, что истинность и ложность есть отношения равного статуса между знаками и обозначаемым.
В таком случае можно сказать, к примеру: «p» истинно означает то, что «~p» означает ложно, и т. п.
4.062. Разве ложными суждениями невозможно добиться понимания, как добиваются его суждениями истинными? До тех пор, пока они мыслятся как ложные? Нет! Суждение истинно, если мы используем его для описания конкретной позиции, имеющей место быть: если под «p» мы разумеем «~p» и все обстоит именно так, тогда, в конкретном случае, «p» истинно, а не ложно.
4.0621. Важно, что знаки «p» и «~p» могут сообщать одно и то же. Это доказывает, что в реальности ничто не соответствует знаку «~».
Отрицания в суждении недостаточно для того, чтобы показать смысл выражения«(~~p = p)».
Суждения «p» и «~p» имеют противоположный смысл, однако им соответствует одна и та же реальность.
4.063. Аналогия, иллюстрирующая понятие истинности: представьте черное пятно на белой бумаге. Можно описать это пятно, указав для каждой точки бумаги, белая она или черная. Тогда черной точке будет соответствовать положительный факт, а белой (не-черной) – отрицательный факт. Если я обозначу точку на листе бумаги (значение истинности, по Фреге), она будет соответствовать предположению, которое подлежит оценке, и т. д.
Но чтобы иметь возможность сказать, что точка черная или белая, я должен знать, когда точку называют черной, а когда – белой; чтобы иметь возможность сказать, что «p» истинно или ложно, я должен определить, при каких обстоятельствах я называю «p» истинным, и тем самым я определяю смысл суждения. Сходство заканчивается вот где: мы можем указать точку на бумаге, даже не зная, что есть черное и белое, однако, если суждение не имеет смысла, ему ничто не соответствует, поскольку оно не обозначает объект (не имеет значения истинности), свойства которого могли бы называться «истинными» или «ложными». Глагол в суждении не истинный и не ложный, вопреки мнению Фреге; то, что истинно, должно содержать глагол.
4.064. Всякое суждение должно иметь смысл; последний нельзя придать утверждением. Смысл суждения – именно то, что оно утверждает. То же применимо к отрицанию и т. д.
4.0641. Могут сказать, что отрицание должно соотноситься с логическим местом, определяемым отрицательным суждением.
Отрицательное суждение определяет логическое место, отличное от места этого суждения.
Отрицательное суждение определяет логическое место при помощи логического места отрицательного суждения. Оно описывает первое, пребывая вне последнего.
Отрицательное суждение может отрицаться, что показывает, что отрицание является суждением, а не просто чем-то дополняющим суждение.
4.1. Суждение представляет существование или не-существование позиции.
4.11. Совокупность истинных суждений есть наука в ее полноте (свод естественных наук).
4.111. Философия не принадлежит к естественным наукам. (Слово «философия» должно обозначать нечто, чье место выше или ниже естественных наук, а не рядом с ними.)
4.112. Цель философии – логическое прояснение мыслей.
Философия – не учение, а деятельность.
Философская работа состоит прежде всего в объяснении.
Философия не сводится к «философским суждениям», но служит прояснению суждений.
Без философии наши мысли туманны и неотчетливы; ее задача – прояснить мысли и придать им четкие границы.
4.1121. Психология не более близка философии, чем любая естественная наука.
Теория познания есть философия психологии.
Разве мое изучение знаковых языков не соотносится с изучением мыслительных процессов, которые философы полагают существенным для философии логики? Вот только в большинстве случаев они углубляются в несущественные психологические исследования, и с моим методом тоже имеется подобный риск.
4.1122. Теория Дарвина имеет к философии не большее отношение, чем любая другая гипотеза из области естественных наук.
4.113. Философия ставит пределы спорной территории естественных наук.
4.114. Она должна ставить пределы мыслимому и, в процессе постановки пределов, также и тому, что не мыслимо.
Она должна ставить пределы тому, что не мыслимо, посредством преодоления мыслимого.
4.115. Она обозначает то, что не может быть сказано, ясно представляя то, что может быть сказано.
4.116. Все, что мыслимо, должно мыслиться ясно. Все, что может быть передано словами, должно передаваться ясно.
4.12. Суждения могут представлять реальность в ее полноте, но не могут представлять то общее, что они должны иметь с реальностью, чтобы обладать способностью ее представлять – логическую форму.
Чтобы представлять логическую форму, мы должны вынести суждения куда-то за пределы логики, то есть за пределы мира.
4.121. Суждения не могут отображать логическую форму, она отражается в них, как в зеркале.
Что находит свое отражение в языке, язык не может представлять.
Что выражает себя в языке, мы не можем выразить посредством языка.
Суждения показывают логическую форму реальности.
Они ее отражают.
4.1211. Так, суждение «fa» показывает, что объект «а» входит в его смысл; два предложения «fa» и «ga» показывают, что один и тот же объект упоминается в обоих.
Если два суждения противоречат друг другу, это отражается в их структуре; и то же верно, если одно из них следует из другого. И т. д.
4.1212. Что может быть показано, о том не следует говорить.
4.1213. Теперь мы также понимаем свое ощущение, что мы обладаем корректным логическим подходом, когда в нашем знаковом языке все соответствует правильно.
4.122. В известном смысле мы можем рассуждать о формальных свойствах объекта и позиций или, в случае фактов, о структурных свойствах; и в том же смысле о формальных и структурных отношениях. (Вместо «структурных свойств» я могу употребить сочетание «внутренние свойства», а вместо «структурных отношений» – «внутренние отношения».
Я ввожу эти формулировки, чтобы указать источник распространенного среди философов смешивания внутренних отношений и собственно отношений, то есть внешних.)
Невозможно, однако, утверждать посредством суждений, что подобные внутренние свойства и отношения присущи объектам: они проявляются, скорее, в суждениях, которые отображают соответствующие позиции и связаны с соответствующими объектами.
4.1221. Внутреннее свойство факта можно также назвать чертой факта (в том смысле, в каком мы говорим о чертах лица, к примеру).
4.123. Свойство является внутренним, если немыслимо, что объект не может им не обладать.
(Этот и тот оттенки синего находятся, eo ipso[2], во внутреннем отношении светлого и темного. Немыслимо, чтобы они не находились в подобном отношении.)
(Отсюда нестрогому употреблению слова «объект» соответствует нестрогое употребление слов «свойство» и «отношение».)
4.124. Существование внутреннего свойства возможной ситуации не выражается посредством суждения; скорее, оно выражает себя в суждении, отображающем ситуацию, посредством внутреннего свойства этого суждения.
Равно бессмысленно утверждать, что суждение обладает формальным свойством, и отрицать это.
4.1241. Невозможно отличить одну форму от прочих, утверждая, что одна имеет такое свойство, а другая – такое свойство; ибо отсюда следует, что мыслимо приписывать каждой форме каждое свойство.
4.125. Существование внутреннего отношения между возможными ситуациями выражается в языке посредством внутреннего отношения между суждениями, их отображающими.
4.1251. Тут кроется ответ на спорный вопрос, являются ли все отношения внутренними или внешними.
4.1252. Я называю последовательность, упорядоченную внутренним отношением, последовательностью форм.
Числовой ряд упорядочен не внешним, а внутренним отношением. То же верно для суждений
«aRb»,
«(Ǝ х): aRx × xRb»,
«(Ǝ x, y): aRx × xRy × yRb», и т. д.
(Если b находится в одном из таких отношений к a, я называю b следующим за a.)
4.126. Теперь мы можем говорить о формальных понятиях в том же смысле, в каком говорим о формальных свойствах.
(Я ввожу это название, чтобы указать на присущее традиционной логике смешивание формальных понятий и собственно понятий.)
Когда нечто оказывается в формальном понятии в качестве его объекта, это нельзя выразить через суждение. Вместо того оно показывается в знаке объекта. (Имя показывает, что оно обозначает объект, цифра показывает, что обозначает число, и т. п.) Формальные понятия на самом деле невозможно представить через функции, как собственно понятия.
По своим характеристикам формальные свойства не могут быть выражены функциями.
Выражение формального свойства есть черта конкретного символа.
И знак характеристики формального понятия есть отличительная черта всех символов, чье значение соответствует этому понятию.
Потому выражение формального понятия есть пропозициональная переменная, в которой постоянна лишь эта отличительная черта.
4.127. Пропозициональная переменная обозначает формальное понятие, а ее значение обозначает объект, подпадающий под понятие.
4.1271. Всякая переменная есть знак формального понятия. Поскольку каждая переменная отображает постоянную форму, которой обладают все ее значения, и это можно трактовать как формальное свойство этих значений.
4.1272. Так, переменное имя «x» есть знак, соответствующий псевдопонятию «объект».
Всякий раз, когда слово «объект» («предмет», «явление» и т. п.) используется корректно, оно выражается в понятийной записи переменным именем.
Например, в суждении «Есть 2 объекта, которые…», оно выражается как «(Ǝx, y)…».
Всякий раз, когда оно используется отлично, как собственно понятийное слово, результатом оказываются бессмысленные псевдосуждения.
Нельзя сказать, к примеру, «есть объекты», как говорят «есть книги». И точно так же нельзя сказать: «Есть 100 объектов» или «Есть א объектов». И бессмысленно рассуждать об общем количестве объектов.
То же относится к словам «сложный», «факт», «функция», «число» и т. д.
Все они обозначают формальные понятия и представляются в понятийной записи переменными, а не функциями и не классами (как полагали Фреге и Рассел).
«1 – число», «Есть только один нуль» и прочие подобные выражения бессмысленны. (Равно бессмысленно говорить «Есть только одна 1» или «2 + 2 в три часа равно 4».)
4.12721. Формальное понятие задано вместе с объектом, который под него подпадает. Поэтому невозможно ввести в качестве элементарных идей объекты, принадлежащие формальным понятиям, и само формальное понятие. И так же невозможно, например, ввести в качестве элементарной идеи понятие функции и конкретные функции, что делает Рассел; или понятие числа и конкретные числа.
4.1273. Если мы хотим выразить в понятийной записи общее суждение «b следует за a», нам требуется выражение общего в последовательности форм
aRb,
(Ǝ х): aRx × xRb,
(Ǝ x, y): aRx × xRy × yRb, …
Чтобы выразить общее последовательности форм, мы должны использовать переменную, поскольку понятие «общее последовательности форм» есть формальное понятие. (Именно это упустили Фреге и Рассел: способ, каким они хотели выражать общие суждения, наподобие приведенного выше, некорректен; он содержит порочный круг.)
Мы можем определить общее последовательности форм, задав первый член последовательности и общую форму операции, которая порождает следующий член из суждения, ему предшествующего.
4.1274. Спрашивать, существует ли формальное понятие, бессмысленно. Ибо никакое суждение не может быть ответом на подобный вопрос.
(Нельзя, например, спросить: «Существуют ли не поддающиеся анализу субъектно-предикатные суждения?»)
4.128. Логические формы не имеют исчисления.
Поэтому в логике нет привилегированных чисел, как нет и возможности философского монизма или дуализма и т. п.
4.2. Смысл суждения заключен в его соотнесенности или несоотнесенности с возможностью существования или не-существования позиций.
4.21. Простейшая разновидность суждения, элементарное суждение, утверждает существование позиции.
4.211. Признак элементарного суждения – ему не противоречит никакое другое элементарное суждение.
4.22. Элементарное суждение состоит из имен. Это сочетание, сцепление имен.
4.221. Очевидно, что анализ суждений должен приводить к элементарным суждениям, состоящим из имен, связанных непосредственно.
Отсюда вопрос, как воплощаются подобные связи в суждении.
4.2211. Даже если мир бесконечно сложен и каждый факт состоит из бесконечного множества позиций, а каждая позиция включает в себя бесконечное множество объектов, всегда будут объекты и позиции.
4.23. Лишь в составе элементарного суждения имя входит в суждение.
4.24. Имена являются простыми символами: я обозначаю их отдельными буквами («x», «y», «z»).
Я записываю элементарные суждения как функции имен, и они имеют форму «fx», «φ (x, y)» и т. д.
Или же я присваиваю им буквы «p», «q», «r».
4.241. Используя два знака с одним и тем же значением, я выражаю это постановкой между ними знака «=».
Так, «a = b» означает, что знак «b» может быть заменен знаком «a».
(Если я использую уравнение, чтобы ввести новый знак «b», предполагая, что он заменит уже имеющийся знак «a», тогда, подобно Расселу, я записываю уравнение-определение в форме «a = b Def». Определение есть правило действий со знаками.)
4.242. Выражения в форме «a = b» суть, таким образом, простые представления. Они ничего не говорят о значениях знаков «a» и «b».
4.243. Можем ли мы понять два имени, не зная, обозначают ли они одно и то же или различное? Можем ли мы понять суждение, в котором встречаются два имени, не зная, одинаковы их значения или различны?
Предположим, мне известны значения английского и немецкого слов, которые обозначают то же самое; я не могу не признать, что они означают одно и то же; в этом случае я должен суметь перевести одно слово в другое.
Выражения вида «a = a» и их производные не являются элементарными суждениями и ни в каком отношении не имеют смысла.
(Это станет очевидно позднее.)
4.25. Если элементарное суждение истинно, позиция существует; если элементарное суждение ложно, позиция не существует.
4.26. Если заданы все истинные элементарные суждения, мы получим полное описание мира. Мир полностью описывается заданием всех элементарных суждений и указанием, какие из них истинны, а какие ложны.
4.27. Для n числа позиций имеются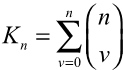 
возможностей существования и несуществования.
Из этих позиций любая комбинация может существовать, а прочие – не существовать.
4.28. Этим комбинациям соответствует равное число возможностей истинности и ложности для n элементарных суждений.
4.3. Возможность истинности элементарных суждений означает возможность существования или не-существования позиций.
4.31. Мы можем представить возможности истинности схемой следующего вида («И» значит «истинно», «Л» значит «ложно», столбцы знаков «И» и «Л» под строками элементарных суждений символизируют их возможности истинности наглядным образом).
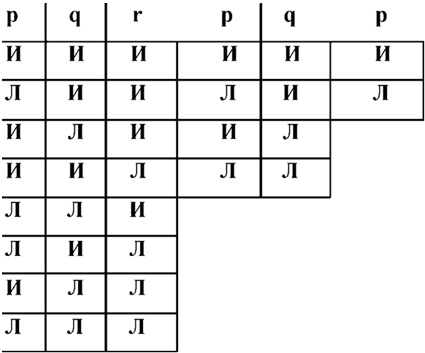
4.4. Суждение есть выражение соотнесенности или несоотнесенности с возможностями истинности элементарных суждений.
4.41. Возможности истинности элементарных суждений суть условия истинности или ложности суждений.
4.411. Сразу становится очевидным, что введение элементарных суждений создает основу для понимания всех прочих суждений. В самом деле понимание общих суждений ощутимо зависит от понимания элементарных суждений.
4.42. Для n числа элементарных суждений имеется
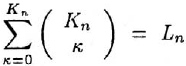
вариантов, какими суждение может соотноситься или не соотноситься с возможностями истинности.
4.43. Соответствие возможностям истинности можно выразить индексом «И» в приведенной выше схеме. Отсутствие этого индекса означает несоответствие.
4.431. Выражение соотнесенности или несоотнесенности с возможностями истинности элементарных суждений обозначает условия истинности суждения.
Суждение есть выражение условий его истинности. (И Фреге был абсолютно прав, используя их как отправную точку для объяснения знаков своей понятийной записи. А вот в объяснении понятия истинности Фреге допустил ошибку: если «истинное» и «ложное» – реальные объекты и аргументы в формуле ~p и т. д., тогда метод, каким Фреге определял смысл «~p», оставил бы их неопределенными.)
4.44. Знак, который получается из сопоставления индекса «И» с возможностями истинности, есть пропозициональный знак.
4.441. Очевидно, что совокупность знаков «И» и «Л» не имеет объекта (или совокупности объектов), сопоставленных ей, как ничто не сопоставлено вертикальным и горизонтальным линиям в таблице или скобкам. Нет никаких «логических объектов».
Разумеется, то же применимо ко всем знакам, выражающим то, что выражают знаки «И» и «Л» в таблице.
4.442. Например, следующее есть пропозициональный знак.
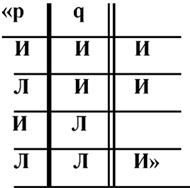
(Знак утверждения Фреге «⊢» логически не имеет значения; в работах Фреге (и Рассела) он просто указывает, что эти авторы считают суждения, отмеченные таким знаком, истинными. Поэтому «⊢» является составной частью суждения не более чем, допустим, номер суждения. Невозможно, чтобы суждение утверждало свою истинность.)
Если последовательность возможностей истинности в таблице фиксирована при помощи комбинаторного правила раз и навсегда, тогда последний столбец сам по себе будет выражением условия истинности. Если записать этот столбец в строку, пропозициональный знак приобретет вид
«(ИИ – И) (p, q)»,
или, более наглядно,
«(ИИЛИ) (p, q)».
(Число мест в левых скобках определяется числом членов выражения в правых скобках.)
4.45. Для n элементарных суждений имеется Ln возможных групп условий истинности.
Группы условий истинности, извлекаемые из возможностей истинности заданного числа элементарных суждений, можно организовать в последовательности.
4.46. Среди возможных групп условий истинности есть два предельных случая.
В одном случае суждение истинно для всех возможностей истинности элементарного суждения. И мы говорим, что условия истинности тавтологичны.
Во втором случае суждение ложно для всех возможностей истинности, и условия истинности противоречивы.
В первом случае мы называем суждение тавтологией, во втором – противоречием.
4.461. Суждения показывают, о чем они говорят; тавтологии и противоречия показывают, что они не говорят ни о чем. Тавтология не имеет условий истинности, поскольку она безусловно истинна; а противоречие не может быть истинным ни при каких условиях.
Тавтология и противоречие не имеют смысла.
(Подобно точке, из которой две стрелки расходятся в противоположных направлениях.)
(Например, я не знаю ничего относительно погоды, когда знаю, что дождь то ли идет, то ли не идет.)
4.4611. При этом тавтология и противоречие не бессмысленны. Они являются частью символики, как нуль является частью символики арифметики.
4.462. Тавтология и противоречие не могут быть картинами реальности. Они не отображают возможные ситуации. Потому что первая признает все возможные ситуации, а последняя не признает ни одну.
В тавтологии условия соотнесенности с миром – условия отображения – отменяют друг друга, и потому она не находится ни в каком отношении отображения к реальности.
4.463. Условия истинности суждения определяют область, которую суждение предоставляет фактам.
(Суждение, картина, модель выступают в отрицательном смысле, как твердое тело, которое препятствует свободе движения, а в положительном смысле – как пространство, окруженное твердой субстанцией, в котором есть место для тела.)
Тавтология предоставляет реальности всю бесконечность логического пространства; противоречие заполняет логическое пространство собой, не оставляя места реальности. Поэтому ни одно из них не способно как бы то ни было определить реальность.
4.464. Истинность тавтологии достоверна, суждения – возможна, противоречия – невозможна.
(Достоверно, возможно, невозможно – вот первое указание на шкалу, которая необходима для теории вероятности.)
4.465. Логическое произведение тавтологии и суждения говорит то же, что само суждение. Это произведение потому тождественно суждению. Ведь невозможно изменить то, что существенно для символа, не изменив смысл последнего.
4.466. Определенной логической комбинации знаков соответствует определенная логическая комбинация их значений. Лишь знакам, не включенным в комбинации, может соответствовать любая комбинация.
Иными словами, суждения, истинные для любой ситуации, не могут быть комбинациями знаков, поскольку в противном случае им соответствовали бы сугубо конкретные комбинации объектов.
(А то, что не является логической комбинацией, не имеет соотнесенности с объектами.)
Тавтология и противоречие суть предельные случаи – точнее, распад – знаковых комбинаций.
4.4661. Допустим, что знаки по-прежнему сочетаются друг с другом в тавтологии и противоречии – что они находятся в определенных отношениях друг к другу; эти отношения не имеют смысла, они несущественны для символа.
4.5. Теперь возможно вывести наиболее общую пропозициональную форму: то есть дать описание суждений любого знакового языка таким образом, что любой возможный смысл может быть выражен символом, удовлетворяющим описанию, и всякий символ, удовлетворяющий описанию, может выразить смысл при условии, что значения имен были подобраны соответственно.
Очевидно, что лишь существенное для наиболее общей пропозициональной формы может быть включено в ее описание – иначе это уже не будет наиболее общей формой.
Существование общей пропозициональной формы доказывается тем фактом, что нет суждения, формы которого нельзя было бы предугадать (то есть сконструировать). Общая форма суждения такова: что-либо имеет место.
4.51. Предположим, что мне задали все элементарные суждения; тогда я просто спрошу: какие суждения я могу составить из них? И у меня были бы все суждения, и так устанавливались бы их границы.
4.52. Суждения включают все, что следует из совокупности элементарных суждений (и, конечно, из того обстоятельства, что это совокупность их всех).
(Так, в известном смысле, можно сказать, что все суждения суть обобщения элементарных суждений.)
4.53. Общая пропозициональная форма – переменная.
5. Суждение – функция истинности элементарных суждений. (Элементарное суждение есть собственная функцияистинности.)
5.01. Элементарные суждения выступают аргументами истинности суждений.
5.02. Аргументы функций нередко смешивают с индексами имен. Поскольку и аргументы, и индексы позволяют узнавать значения знаков, их содержащих.
Например, когда Рассел пишет: «+ c», «c» представляет собой индекс, который указывает, что данный знак есть дополнительный знак количественного числа. Но использование этого знака является результатом произвольной договоренности, и вполне возможно выбрать простой знак вместо «+c»; но в выражении «~p» «p» является не индексом, а аргументом: смысл выражения «~p» нельзя понять до тех пор, пока нам неизвестен смысл «p». (В имени «Юлий Цезарь» индексом будет «Юлий». Индекс всегда часть описания объекта, к имени которого мы его прибавляем; в данном случае Цезарь из рода Юлиев.)
Если я не ошибаюсь, теория Фреге относительно значения суждений и функций основана на смешении аргументов и индексов. Фреге рассматривал логические суждения как имена, а их аргументы – как индексы этих имен.
5.1. Функции истинности могут организовываться в последовательности. Вот основа теории вероятности.
5.101. Функции истинности заданного числа элементарных суждений всегда можно отразить в схеме следующего вида:
(ИИИИ) (p, q) Тавтология (если p, то p, и если q, то q) (p ⊃ p × q ⊃ q)
(ЛИИИ) (p, q) Словами: Не p и не q вместе. [~ (p × q)]
(ИЛИИ) (p, q) Словами: Если q, то p. [q ⊃ p]
(ИИЛИ) (p, q) Словами: Если p, то q. [p ⊃ q]
(ИИИЛ) (p, q) Словами: p или q. [p ∨ q]
(ЛЛИИ) (p, q) Словами: Не q. [~q]
(ЛИЛИ) (p, q) Словами: Не p. [~p]
(ЛИИЛ) (p, q) Словами: p или q, но не вместе. [p × ~q: ∨: q × ~p]
(ИЛЛИ) (p, q) Словами: Если p, то q, и если q, то p. [p ≡ q]
(ИЛИЛ) (p, q) Словами: p.
(ИИЛЛ) (p, q) Словами: q.
(ЛЛЛИ) (p, q) Словами: Ни p, ни q. [~p × ~q или p | q]
(ЛЛИЛ) (p, q) Словами: p, но не q. [p × ~q]
(ЛИЛЛ) (p, q) Словами: q, но не p. [q × ~p]
(ИЛЛЛ) (p, q) Словами: q и p. [q × p]
(ЛЛЛЛ) (p, q) Противоречие (p и не p, и q и не q).[p × ~p. q × ~q]
Я назову основаниями истинности суждения те возможности истинности его истинностных аргументов, которые делают суждение истинным.
5.11. Если все основания истинности, общие какому-либо числу суждений, являются и основаниями истинного некоего конкретного суждения, мы говорим, что истинность этого суждения следует из истинности других.
5.12. В частности, истинность суждения «p» следует из истинности суждения «q», если все основания истинности последнего являются и основаниями истинности первого.
5.121. Основания истинности одного содержатся в основаниях истинности другого: p следует из q.
5.122. Если p следует из q, значение «p» содержится в значении «q».
5.123. Если бог создает мир, в котором истинны некие суждения, тем самым он создает и мир, в котором будут истинны все суждения, следующие из первых. При этом он не может создать мир, в котором суждение «p» будет истинно, не создав все его объекты.
5.124. Суждение подтверждает любое другое суждение, которое из него следует.
5.1241. «(p × q)» – суждение, которое подтверждает одновременно «p» и «q».
Два суждения противопоставляются друг другу, если нет осмысленного суждения, подтверждающего оба.
Всякое суждение, противоречащее другому, его отрицает.
5.13. Когда истинность одного суждения следует из истинности других, мы видим это по структуре суждения.
5.131. Если истинность одного суждения следует из истинности других, это находит выражение в отношениях, в которых пропозициональные формы находятся друг с другом; для нас нет необходимости устанавливать эти отношения, объединяя формы в одном суждении. Эти отношения являются внутренними, их существование непосредственно вытекает из существования суждений.
5.1311. Когда мы выводим q из (p ∨ q) и ~p, отношение между пропозициональными формами «p ∨ q» и «~p» скрыто способом обозначения. Но если вместо «p ∨ q» мы запишем, например, «p | q × | | × p | q», а вместо «~p» – «p | p» (p | q = ни p, ни q), тогда внутренняя связь станет очевидной.
(Возможность вывода fa из (x) × fx показывает, что символ «(x) × fx» содержит в себе всеобщность.)
5.132. Если p следует из q, я могу заключить от q к p, вывести p из q.
Природа взаимосвязи проявляется лишь в двух суждениях.
Они сами являются единственными возможными оправданиями вывода.
«Законы вывода», которые должны оправдывать вывод, как в работах Фреге и Рассела, лишены смысла и потому излишни.
5.133. Все выводы делаются априорно.
5.134. Элементарное суждение нельзя вывести из другого элементарного суждения.
5.135. Нет способа из существования одной ситуации сделать вывод о существовании другой, полностью отличной ситуации.
5.136. Не существует причинной связи, оправдывающей подобный вывод.
5.1361. События будущего нельзя вывести из событий настоящего. Суеверие есть вера в подобную причинную связь.
5.1362. Свобода воли состоит в невозможности знания действий, лежащих в будущем. Мы могли бы узнать их, только будь причинность внутренней необходимостью, как в случае логического вывода. Связь между познанием и тем, что известно, есть связь «логической необходимости».
