Жак Виллен
Физика повседневности. От мыльных пузырей до квантовых технологий

Глава 4

Маятник Фуко и сила Кориолиса

В начале XIX века все были уверены, что Земля шарообразна и вращается вокруг своей оси, но экспериментальных свидетельств этому не имелось. Первым неоспоримым доказательством этих фактов стал известный опыт Леона Фуко.

Вращение Земли вокруг своей оси объясняет многие явления, например из области метеорологии и океанографии. Чтобы понять природу этих явлений, нужно научиться их описывать теоретически. Для этого физики прибегают к использованию фиктивной силы, называемой именем Гаспара-Гюстава де Кориолиса.

В 1851 году парижский Пантеон стал местом проведения эксперимента, осуществленного физиком Леоном Фуко (1819–1868). К верхней части купола, на подвесе длиной 67 м, он прикрепил шар массой в 28 кг, создав таким образом маятник (илл. 1), аналогичный балансиру часов наших прабабушек и прадедушек. В отличие от маятника часов, который способен двигаться только в определенной вертикальной плоскости, маятник Фуко мог свободно колебаться в любых направлениях. Эксперимент предполагал отклонить маятник от равновесного положения (вертикального), а затем отпустить и позволить ему свободно колебаться. Поскольку трение крайне мало, маятник может очень долго колебаться без затухания. Что же наблюдали экспериментаторы? При первых колебаниях маятник, казалось, оставался в вертикальной плоскости, определенной осью маятника и начальным отклонением. Именно так, как читателя и учили в средней школе. Через несколько минут, однако, ученые заметили, что плоскость качания маятника начала постепенно поворачиваться! При этом поворачивалась она всегда в одном и том же направлении. Давайте поймем, в каком именно.

1. Маятник Фуко, установленный в зале Пантеона в Париже, где в 1851 году и был поставлен опыт Фуко. Отклоненный от равновесного положения, маятник колеблется в плоскости, которая постепенно поворачивается

2. Доказательство вращения Земли с помощью маятника Фуко.

a. Первоначальное положение маятника на Северном полюсе и наблюдателя на Земле.

b. Спустя час Земля относительно звезд повернулась вокруг себя на восток (в направлении фиолетовой стрелки), повернулась и стойка, но плоскость колебаний маятника осталась неподвижной. В то же время для наблюдателя на Земле стойка выглядит сохранившей свое первоначальное положение, а плоскость колебаний маятника кажется повернувшейся

Маятник Фуко на Северном полюсе

Почему же плоскость качания маятника поворачивается? Опыт Фуко легче понять, проведя его для начала на Северном (или Южном) полюсе. Представим себе маятник, равновесное положение которого совпадает с проходящей через полюс земной осью. Отклоним его от начального положения (илл. 2a). Для наблюдателя, неподвижного относительно Солнца и звезд (допустим, что относительное положение звезд не зависит от времени), маятник качается в фиксированной вертикальной плоскости (илл. 2b). Однако это совсем не так для наблюдателя, находящегося на Земле, так как последняя вращается вокруг своей оси, совпадающей в данном случае с вертикалью, на которой находится точка крепления маятника. Таким образом, наблюдатель поворачивается вместе с Землей относительно плоскости колебаний маятника на восток. Не чувствуя, что вращается вместе с планетой, такой наблюдатель считает, что это плоскость колебаний маятника поворачивается, и маятник для него отклоняется к западу (вспомните: для нас Солнце встает на востоке и движется по небосклону на запад. На самом же деле, как мы сегодня хорошо знаем, это земной шар вращается на восток, а Солнце остается почти неподвижным).

Из нашего рассуждения понятно, что на Южном полюсе маятник отклонится к востоку. На полюсе плоскость колебаний маятника выполняет полный оборот за 24 часа^[1]. В Париже же этот процесс занимает значительно больше времени. Разберемся почему.

Сила Кориолиса

Представлять наблюдателя, неподвижного по отношению к звездам, чтобы понять, что видит его коллега, вращающийся вместе с Землей, неудобно. Проще было бы рассуждать только с точки зрения земного наблюдателя, предполагая, что на шар воздействует некая сила, которая заставляет его отклоняться к западу… И мы действительно можем так поступить! Для этого нужно рассматривать движение маятника Фуко в системе координат, или системе отсчета, связанной с Землей. Чтобы учесть вращение Земли вокруг своей оси, следует принять, что на шар, помимо сил веса и реакции нити (подвеса), воздействует еще одна сила. Ее назвали силой Кориолиса в честь французского математика Гаспара-Гюстава де Кориолиса (илл. 3).

3. Гаспар-Гюстав де Кориолис (1792–1843). Одно из немногих известных его изображений выполнено французским художником Бельяром по портрету кисти Роллера. Имя Кориолиса увековечено гравюрой на первом этаже Эйфелевой башни, наряду с еще 71 ученым

Чтобы двигаться дальше, давайте пока оставим в стороне маятник Фуко, колебания которого усложняют необходимые для дальнейшего рассуждения, и вместо него рассмотрим пулю массой m, выпущенную из ружья. Чтобы еще больше облегчить задачу, предположим, что пуля движется по прямой линии, и мы при изучении ее траектории учитываем только влияние вращения Земли. Это предположение является всего лишь искусственным приемом для упрощения дальнейших рассуждений.

Представим, что стрелок находится на Северном полюсе, в точке N (илл. 4), и выпускает в направлении цели C, движущейся вместе с Землей, пулю P с начальной скоростью v. Земля вращается вокруг своей оси с угловой скоростью Ω, равной одному обороту в день. Таким образом, через некоторое время t она провернется на угол Ωt, и цель сдвинется вместе с ней. Тем не менее, с точки зрения стрелка, стоящего на Северном полюсе и глядящего на цель, все происходит так, будто бы последняя осталась на месте, а пуля отклонилась от заданной им траектории NC. Расстояние от P до линии NC в момент t составляет приблизительно произведение угла Ωt на пройденное пулей расстояние vt, то есть Ωvt². В этом рассмотрении мы считаем промежуток времени достаточно коротким, а угловую скорость Ω – измеренной в радианах в секунду.

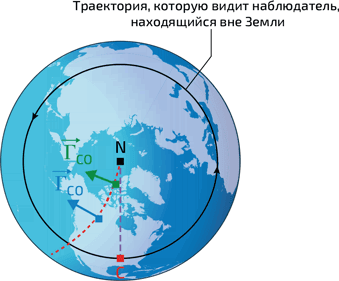
4. Отклонение пули под действием силы Кориолиса в системе отсчета, связанной с Землей. Пуля, выпущенная из ружья на Северном полюсе N в направлении цели C, отклоняется к западу от цели. Для наблюдателя вне Земли траектория пули – прямая линия (фиолетовая). Для наблюдателя, связанного с Землей, траектория представляется красной кривой (ее кривизна здесь сильно преувеличена): действующая на пулю сила Кориолиса придает ей ускорение Г^→_CO, показанное на рисунке в два разных момента

Таким образом, для достаточно малых промежутков времени пуля относительно Земли будет равномерно двигаться в направлении NC со скоростью v и в то же время равноускоренно двигаться вправо, в направлении, перпендикулярном отрезку NC (если бы стрельба производилась на Южном полюсе, то пуля отклонилась бы влево). При этом ускорение, называемое Кориолисовым, оказывается равным 2Ωv (вторая производная по времени от пройденного расстояния Ωvt²). В соответствии со вторым законом Ньютона (см. главу 4, врезку «Ньютоновская механика»), это означает, что на пулю воздействует сила величиной 2Ωvm, сонаправленная ускорению Кориолиса. Это и есть сила Кориолиса.

Ускорение Кориолиса всегда перпендикулярно мгновенной скорости (илл. 4). Напомним, что в рассматриваемой задаче, благодаря действию силы тяжести, имеется еще и вертикальное ускорение, которое мы (в отличие от артиллеристов!) здесь не учитывали.

Уточним, что сила Кориолиса – сила «фиктивная», или, как часто говорят, сила инерции, потому что она не вызвана физическим воздействием одного тела на другое. При описании движения тела во вращающейся системе координат сила Кориолиса должна учитываться всегда, когда скорость тела не направлена вдоль оси вращения.

Прикинем, действительно ли стрелок промахнется мимо цели, если он не учтет силу Кориолиса? Предположим, что цель расположена на расстоянии d = 100 м, а скорость пули составляет v = 1000 м/с. Время, необходимое пуле для достижения цели, t = d/v = 0,1 с. Скорость вращения Земли составляет Ω = 2π радиан/день, что составляет около 0,7∙10^–4 радиан/с. Тогда вызванное силой Кориолиса отклонение есть y = Ωvt² = 0,7 мм. Таким образом, стрелок в рассматриваемом случае не промахнется. Он даже не поймет, что его цель двигалась относительно траектории пули. Можно также вычислить ускорение Кориолиса, равное 2Ωv: оно составляет 0,14 м/с².

Ньютоновская механика

В начале XVII века итальянский ученый Галилео Галилей (1564–1642) сделал первый шаг в понимании законов движения и гравитации. Он показал, что находящийся в свободном падении объект равномерно ускоряется, а также сформулировал принцип инерции: «Тело, которое не подвергается никакому воздействию, сохраняет свое движение по прямой линии с постоянной скоростью, если оно уже находится в движении, или остается неподвижным, если изначально находилось в состоянии покоя». Это утверждение кажется очевидным. Тем не менее со времен Аристотеля считалось, что для движения тела необходимо наличие внешнего воздействия. Вскоре, после Галилея, немецкий астроном Иоганн Кеплер (1571–1630) сформулировал законы, объясняющие движение планет. Первый из этих законов гласит, что планеты в своем движении вокруг Солнца описывают эллипсы, причем Солнце находится в одном из фокусов соответствующего эллипса. Позже англичанин Исаак Ньютон (1643–1727) заложил основы классической механики, основываясь на нескольких простых предположениях.

 

В качестве первого он принял принцип инерции Галилея. Второе предположение, или второй закон Ньютона, который часто называют основным законом динамики, гласит, что ускорение a^→ = dv^→/dt, приобретаемое материальной точкой и умноженное на ее массу m, равно сумме воздействующих на эту точку внешних сил F^→:

Σ F^→ext = ma^→.

Этот закон дает нам основное уравнение движения и позволяет предсказать положение и скорость материальной точки в любой момент времени при условии, что мы знаем, где она находилась и какая у нее была скорость при t = 0.

Казалось бы, из второго закона Ньютона вытекает и первый, достаточно положить нулем сумму приложенных сил. Однако, принцип инерции имеет свой глубокий смысл, который придает ему статус закона. В современной формулировке он звучит так: «Существуют определенные системы отсчета, называемые галилеевыми, по отношению к которым движущийся объект сохраняет постоянную скорость, когда на него не действуют никакие силы, или сумма внешних сил равна нулю». Другими словами, первый закон Ньютона позволяет выбрать такие системы отсчета, в которых будут справедливы второй и третий законы.

Третий закон Ньютона, или принцип действия и противодействия, гласит: «При воздействии одного тела на другое первое испытывает ответное воздействие со стороны второго той же силы, но направленной противоположно».

И наконец, Ньютон сформулировал закон всемирного притяжения (или тяготения). Он научил будущие поколения, что два массивных тела притягиваются с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними (см. главу 5, «Ньютон – основатель современной физики»).

Законы механики Ньютона и сформулированный им закон всемирного тяготения с высокой точностью объяснили все проблемы механики, существовавшие в его время. Например, падение яблока на землю (см. илл. 2 в главе 5) и движение планет вокруг Солнца! Эти законы успешно применялись в астрономии для расчета траектории движения спутников вокруг планет и предсказали возвращение кометы Галлея в 1759 году. К сожалению, многие реальные проблемы часто настолько математически сложны, что возможно только их приблизительное решение. Это относится, например, к задаче о движении трех тел (скажем, Солнца, Земли и Луны) под воздействием взаимного гравитационного притяжения – ее точного решения просто не существует.

Титульный лист журнала Philosophiae Naturalis Principia Mathematica («Математические начала натуральной философии»), опубликованного в 1687 году, в котором Ньютон представил свои фундаментальные законы механики

В метеорологии, которая имеет дело с гораздо меньшими скоростями и намного большими расстояниями, для описания движения воздушных и водных масс сила Кориолиса должна учитываться обязательно. Действительно, вызванное силой Кориолиса отклонение y = Ωvt², введя пройденное расстояние x = vt, можно переписать как y = Ωх²/v. Если расстояние x составляет порядка ста километров, а скорость течения – около 20 км/ч, то отклонение y будет того же порядка, что и x. Например, отклонение из-за силы Кориолиса морского течения, скорость которого v = 6 м/с (около 22 км/ч), составляет порядка 10 км после пройденных 100 км в направлении начальной скорости! Далее в этой главе мы еще вернемся к этому вопросу.

Вдали от полюсов

До сих пор мы предполагали, что наши опыты осуществляются на полюсе. Что произойдет, если удалиться от него?

В нескольких строках уравнений в учебнике механики показано, что сила Кориолиса, действующая на снаряд массой m, движущийся со скоростью v^→ по отношению к Земле, – это вектор, перпендикулярный оси вращения Земли и скорости v^→. При этом его модуль равен

FCO = 2mΩvsinϕ,

где ϕ – угол между осью вращения и скоростью v^→. Направление вектора F^→CO определяется по правилу левой руки (см. главу 4, врезку «Смысл силы Кориолиса и векторное произведение»).

У силы Кориолиса имеется горизонтальная составляющая, которая заставляет поворачиваться плоскость колебаний маятника Фуко и обычно отклоняет движущиеся объекты вправо в Северном полушарии и влево – в Южном. Но у силы Кориолиса есть и вертикальная составляющая, параллельная вектору силы веса предмета. Этой составляющей чаще всего можно пренебречь, потому что для обычных скоростей она, по сравнению с весом тела, мала. Для пули, двигающейся со скоростью 1000 м/с, вертикальная составляющая ускорения Кориолиса составляет максимум 0,14 м/с², что почти в 70 раз меньше ускорения свободного падения g. При полете куда более медленного теннисного мяча вертикальная составляющая ускорения Кориолиса оказывается меньше g уже в тысячи раз!

Смысл силы Кориолиса и векторное произведение

Сила Кориолиса, действующая на объект массой m, может быть удобно выражена в виде векторного произведения его скорости v^→ и вектора угловой скорости Ω^→:

F^→CO = 2mv^→ × Ω^→.

Напомним, что Ω^→ – вектор, характеризующий вращающееся тело (в нашем случае – Земля). Этот вектор параллелен оси вращения, а его модуль равен угловой скорости Ω.

Что означает понятие векторного произведения? Векторное произведение двух векторов v^→ и Ω^→, направленных под углом α, представляет собой третий вектор, ортогональный первым двум, с модулем Ωvsinα. При этом его направление определяется по правилу левой руки (см. илл.).

Векторное произведение используется при описании многих физических явлений, включая электромагнетизм.

Правило левой руки используют, чтобы определять направление векторного произведения F^→ = v^→ × Ω^→. Левая рука помещается перпендикулярно вектору Ω^→ так, чтобы он был направлен в ладонь, в то время как указательный палец должен совпадать с направлением вектора v^→. Отставленный большой палец тогда укажет направление вектора F^→.

a. Случай, где v^→ перпендикулярен оси вращения.

b. Общий случай.

Теперь, когда мы обогатили наши знания, вернемся к маятнику Фуко и к периоду поворота его плоскости колебаний. По формуле FCO = 2mΩvsinϕ можно вычислить горизонтальную составляющую силы Кориолиса, которая составит F^'CO = 2mΩvsinα, где α – широта места проведения эксперимента. Эта составляющая максимальна на Северном полюсе, где sin α = 1; там подтверждается и уже известный нам результат: плоскость колебаний маятника осуществляет свой полный оборот за 24 часа. На экваторе α = 0, и плоскость колебаний маятника Фуко не поворачивается вообще. В других точках Земли период оборота плоскости колебаний таков, каким бы он был на полюсах, если бы период вращения Земли вокруг оси был умножен на sin α, другими словами, если бы продолжительность суток была умножена на 1/sinα. Это означает, что период оборота маятника Фуко, выраженный в часах в зависимости от широты места проведения эксперимента, равен 24/sinα. На 45-й параллели, которая проходит примерно через Женеву, Монреаль и Краснодар, и маятник Фуко поворачивается в раз медленнее, чем на полюсе: вместо 24 часов он совершает полный оборот за

Фуко, Галилей и Аристотель

Среди всех маятников Фуко, существующих в мире, один заслуживает специального упоминания: маятник, находившийся с 1931 по 1986 год в Исаакиевском соборе в Ленинграде. Этот собор был превращен в музей атеизма. Какова же связь между маятником Фуко и религией?

Присутствие маятника Фуко в антирелигиозном учреждении намекало на осуждение Галилея инквизицией в 1633 году (см. илл.). Галилей утверждал, что на самом деле Земля движется вокруг Солнца и поворачивается вокруг своей оси за один день. Кардиналы же уверяли, что, согласно Библии, Иисус некогда остановил вращение Солнца вокруг Земли, но не вращение Земли вокруг своей оси. Также они вынесли следующий приговор: «Вследствие рассмотрения твоей вины и сознания твоего в ней присуждаем и объявляем тебя, Галилей, за все вышеизложенное и исповеданное тобою под сильным подозрением у сего Св. судилища в ереси, как одержимого ложною и противною Священному и Божественному Писанию мыслью, будто Солнце есть центр земной орбиты и не движется от востока к западу, Земля же подвижна и не есть центр Вселенной».

После этого обвинения Галилей должен был отречься от своей теории. Впрочем, провозглашая, что Земля обращается вокруг своей оси, он на самом деле не имел доказательств. Он только обобщил наблюдения Коперника и Кеплера, которые заметили, что астрономические движения описываются проще, если предположить, что Земля вращается! Проведенный в 1851 году опыт Фуко дал прямое доказательство вращения Земли вокруг своей оси и поставил точку в споре, который начался 24 веками раньше, когда Аристотель описал совершенную и вечную Вселенную, в центре которой находится Земля.

На самом же деле Фуко не был первым, кто экспериментально доказал вращение Земли. В 1833 году немецкий ученый Фердинанд Райх бросая камни в шахту глубиной 158 м, констатировал их отклонение после падения от вертикали на 28 мм, что соответствовало последующим результатам применения теории Кориолиса. А в 1661 году, спустя некоторое время после смерти Галилея, знаменитый флорентийский ученый Винченцо Вивиани провел опыт, аналогичный опыту Фуко. Но он его никак не объяснил – либо потому что объяснения не имел, либо из-за страха перед инквизицией.

Галилей на суде инквизиции

Где увидеть маятник Фуко?

Маятник Фуко – настолько занимательный экспонат, что читатель наверняка захочет увидеть его своими глазами (илл. 1). В Париже маятник Фуко был возвращен в Пантеон в 1995 году и доступен для обзора всем желающим, если только не находится в ремонте; еще один можно увидеть в Музее искусств и ремесел^[2].

Почему бы не изготовить собственный маятник Фуко? Это не лучшая идея, так как здесь кроется множество затруднений. Прежде всего, маятник должен быть длинным, чтобы колебания были медленными, что позволит снизить роль трения. Маятник в Ленинграде был самый большой в истории – длина проволоки 98 м! Следовательно, надо иметь очень высокую точку подвеса и суметь надежно прикрепить к ней маятник. Резко отпущенный маятник может начать извиваться, что увеличивает трение. Еще серьезнее другое препятствие: вместо того чтобы оставаться в плоскости, которая медленно поворачивается, маятник может начать описывать вытянутый конус. Научные сотрудники Университета Гренобля, установившие для студентов маятник Фуко в 2013 году, на собственном опыте оценили степень всех этих трудностей.

5. Мотоциклист склоняется внутрь виража чтобы сбалансировать центробежную силу. Чем круче вираж, тем больше угловая скорость вращения ω и, следовательно, значительнее центробежная сила

Еще одна фиктивная сила: центробежная

Еще одной «фиктивной» силой инерции является центробежная сила, проявления которой нам знакомы куда лучше, чем примеры воздействия силы Кориолиса. Она появляется в системе отсчета, вращающейся по отношению к неподвижным звездам, и стремится отбрасывать неподвижные в этой системе отсчета телá от центра вращения. В повседневной жизни эта сила позволяет нам, к примеру, отжимать белье в стиральной машине: вода выбрасывается наружу через дырки барабана. Мы ощущаем ее воздействие также при езде на мотоцикле (илл. 5) или в автобусе, когда он совершает крутой поворот и нас отбрасывает к внешней стороне виража, на соседа.

Чему эта центробежная сила равна? Для нахождения соответствующей формулы давайте рассмотрим ребенка, катающегося на ярмарочной карусели радиусом R, которая крутится с угловой скоростью ω. Ребенок роняет плюшевого медведя, и, если пренебречь силой тяжести, он улетает по касательной со скоростью v = Rω по отношению к земле (из определения угловой скорости). При этом медведь относительно ребенка движется с ускорением, равным v²/R = ω²R. Это ускорение возникает потому, что мы рассматриваем движение медведя во вращающейся системе отсчета. Согласно основному закону динамики (см. главу 4, врезку «Ньютоновская механика»), раз в этой системе у медведя массой m имеется ускорение ω²R, то на него действует сила F^→, равная по модулю mω²R и направленная от центра карусели по радиусу. Это и есть центробежная сила!

Как на ребенка и плюшевого медведя на карусели, на всех нас постоянно действует центробежная сила, вызванная вращением Земли. К счастью, она приблизительно в 300 раз меньше нашего веса, поэтому ее мы почти не замечаем. Из-за воздействия центробежной силы диаметр Земли на экваторе на 43 км больше, чем расстояние от одного полюса до другого, но эта разница составляет примерно 0,3 % и особых последствий не влечет.

С другой стороны, центробежная сила, вызванная вращением Земли, на движение связанных с ней объектов (например на ветер, который является движением воздуха по отношению к почве) не влияет. Действительно, центробежная сила действует и на воздух, и на почву одинаково и зависит только от расстояния до центра вращения. Напротив, сила Кориолиса ничтожна для объекта, связанного с почвой в наземной системе отсчета, однако воздействует на движущийся воздух. В итоге, как мы сейчас увидим, она играет важную роль в метеорологии.