Жак Виллен
Физика повседневности. От мыльных пузырей до квантовых технологий

Полная версия

Цвет неба в хорошую погоду

В то время как предсказать цвет моря непросто, цвет неба в хорошую погоду легко объясняется физическими принципами, выявленными английским физиком лордом Рэйли (Рэлеем) (1842–1919). В отсутствие облаков цвет неба определяется результатом взаимодействия солнечного излучения с компонентами атмосферы Земли, а именно с неоднородностями (флуктуациями) плотности молекул азота и кислорода.

Как эти молекулы ведут себя, попав в поле солнечного излучения? Рассмотрим монохроматический свет, обладающий заданной длиной волны λ. Он представляет собой колеблющиеся в плоскостях, перпендикулярных направлению распространения света, с частотой υ магнитное и электрическое поля. Под действием колеблющегося электрического поля электроны в молекулах также колеблются с частотой υ. В результате и сама молекула становится маленьким излучателем, испуская свет той же частоты, что и падающая волна. Это похоже на то, как излучает электромагнитные радиоволны теле- или радиоантенна. В случае молекул и солнечного света длина его волны оказывается много большей размера молекул, и такое рассеяние называется «рассеянием Рэлея». Расчеты показывают, что интенсивность рассеянного света оказывается пропорциональной четвертой степени частоты υ⁴ (или 1/λ⁴). Это утверждение называется законом Рэлея – Джинса (илл. 2).

2. Рассеяние света молекулами и закон Рэлея. Под воздействием падающего монохроматического света (a) молекулы переизлучают свет той же длины волны во всех направлениях. Синему цвету соответствует длина волны около 450 нм, а красному – около 650 нм. (b) Согласно закону Рэлея, четвертая степень отношения 650/450 равна 4,3, то есть интенсивность рассеяния синего примерно в 4 раза выше, чем красного

Как все это связано с цветом неба? Согласно закону Рэлея, рассеяние электромагнитных волн оказывается значительно интенсивнее для высоких частот по сравнению с низкими. Это означает, что молекулы атмосферы сильнее рассеивают синий цвет, чем красный, зеленый или желтый. Таким образом, наших глаз преимущественно достигают именно световые лучи синего цвета. Вот почему небо синее! Следуя этому рассуждению, можно было бы предположить, что небо должно быть фиолетовым, так как фиолетовое излучение обладает более высокой частотой, чем синее. В действительности в спектре солнечного излучения доля фиолетового меньше, чем синего. Кроме того, и максимальная чувствительность человеческого глаза находится в области зеленого (555 нм). В результате фиолетовая часть спектра солнечного излучения оказывается подавленной в восприятии человеческого глаза, и небо видится синим (см. главу 3, «Цветовое зрение»).

3. a. Днем чистое небо кажется синим, так как молекулы атмосферы сильно рассеивают синюю компоненту солнечного излучения.

b. На закате доходящий до нас солнечный свет преодолевает гораздо более толстый слой атмосферы, и небо пламенеет

Небо на закате… и после

На закате небо над горизонтом принимает красивый розовый оттенок (илл. 3). Этот цвет также обусловлен рассеянием солнечного света в атмосфере. Поскольку свет распространяется во всех направлениях, то до нас доходит лишь его часть, а остальное возвращается в пространство. Часть солнечной энергии, возвращающаяся за пределы земной атмосферы, невелика, однако для некоторых явлений она может оказаться существенной (илл. 4). В видимом излучении разница между энергией, получаемой поверхностью земли и верхними слоями атмосферы, обусловлена прежде всего рассеянием. Так, мы видим, что в дневное время энергия, получаемая на земле, меньше падающей на верхние слои атмосферы примерно на 25 % в синем и на 10 % – в красном диапазонах. На закате эти пропорции изменяются, поскольку свету приходится преодолевать гораздо большую толщу атмосферы (илл. 5). Таким образом, синий свет почти целиком рассеивается, и наблюдатель на земле видит в основном красный.

Как только солнце исчезает за горизонтом, постепенно наступает ночь. Цвет неба в ночное время – совсем иной вопрос (см. главу 3, «Тайны безлунной ночи»).

Цвет облаков

Как можно увидеть на картине Рылова (см. илл. 1 в главе 3), облака бывают белые, серые или черноватые, в зависимости от их толщины и места, откуда их наблюдают. В любом случае они непрозрачны: солнце не видно сквозь облака, а солнечный свет оказывается более или менее интенсивным в зависимости от их толщины. Он доходит до нас, рассеянный каплями воды, из которых состоит облако. Такое рассеяние намного более интенсивно, чем рассеяние на флуктуациях плотности молекул кислорода и азота, которое мы описали выше. Почему?

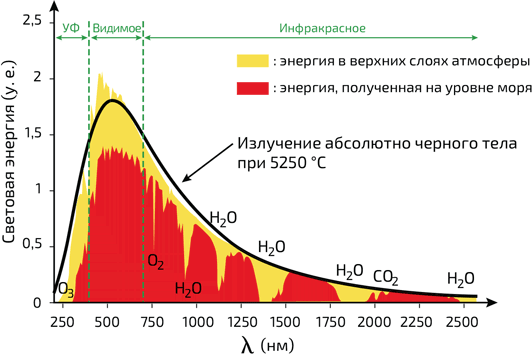
4. Световая энергия, получаемая верхними слоями атмосферы (желтый) и на уровне моря (красный) в дневное время с учетом рассеяния и поглощения. Отметки «H₂O» и «O₂» обозначают диапазон поглощения воды и кислорода соответственно. Энергия, отложенная по оси ординат, выражается в ваттах на кв. м поверхности, в то время как длины волн на оси абсцисс измеряются в нанометрах

Причина в том, что большие объекты рассеивают свет намного сильнее, чем маленькие. Например, если капля воды содержит миллион молекул (и имеет диаметр около 0,04 мкм), она рассеивает свет почти в миллион миллионов раз интенсивнее, чем миллион отдельных молекул! Получается, что если в капле миллиард молекул, то она рассеивает свет в миллиард миллиардов раз больше, чем такое же число изолированных молекул? Нет! Диаметр этой капли составляет порядка 0,4 мкм – величина существенная по сравнению с длиной волны видимого света. Закон «голубого неба» Рэлея в этом случае неприменим, поскольку переизлучение света каждой из молекул воды, находящейся в капле, случайно по фазе. Последнее обстоятельство приводит к ослабляющей интерференции этих вторичных волн – явлению, о котором мы поговорим чуть позже. Расчет интенсивности рассеяния электромагнитного излучения на сфере произвольного радиуса R был впервые выполнен немецким физиком Густавом Ми в 1908 году. Точный результат представляется бесконечной суммой слагаемых. Для небольшой капли (R << λ) в этой сумме можно сохранить лишь первое слагаемое, которое и соответствует рассеянию Рэлея. Чем больше капля, тем больше количество слагаемых, которые следует учитывать. При R >> λ расчет упрощается: в этом случае применяется геометрическая оптика. Согласно очевидным геометрическим соображениям, количество энергии света, падающей на сферу, пропорционально ее сечению, то есть R². Таким образом, на большую каплю падает больше энергии, чем на меньшую; в меру квадрата своего радиуса она больше света и переизлучает. Кроме того, оказывается, что общая интенсивность света, рассеиваемого большой каплей, не зависит от длины падающей волны. Именно это и объясняет тот факт, что при падении на систему капель белого света и рассеянный свет также оказывается белым. Итак, облака белые, потому что белым является освещающий их солнечный свет!

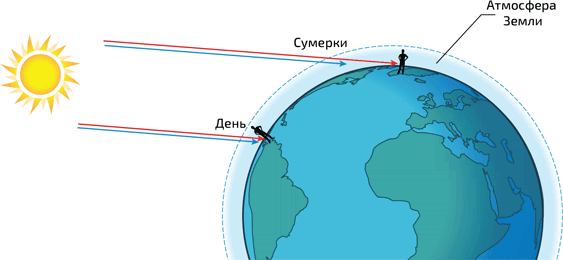
5. Испускаемое Солнцем излучение с большими длинами волн в красной части спектра рассеивается меньше, чем излучение с короткими длинами волн в синей части. Поэтому в сумерках падающий под малым углом синий луч сильно рассеивается в атмосфере и доходит до Земли приглушенным, в отличие от красного. Днем же все цвета солнечного излучения достигают земной поверхности. (Пропорции не соблюдены.)

Тайны безлунной ночи

Без Луны ночное небо черное, с разрозненными звездами. Это кажется нормальным. Но в небе колоссальное количество звезд, может быть, даже бесконечное. Бесконечное число звезд должно производить бесконечное сияние. Что, если черное небо – признак конца Вселенной? Именно это предположил немецкий ученый Иоганн Кеплер в начале XVII века. В XIX веке другой немец, Генрих Ольберс, заметил, что ближайшие звезды, вероятно, скрывают более далекие, поэтому, даже если Вселенная бесконечна, ее светимость будет не бесконечной… но все же очень большой! На сегодняшний день объяснение этого парадокса заключается в том, что Вселенная имеет конечный возраст. Она появилась в результате Большого взрыва, характеризующегося высокой плотностью и температурой и произошедшего 13,8 миллиардов лет назад. После этого Вселенная начала расширяться. В результате длина световых волн, излучаемых далекими галактиками, смещается к красному концу спектра. Кроме того, при наблюдении за отдаленными объектами из-за конечности скорости света мы «обгоняем время»: галактики предстают перед нами в том состоянии, в котором они были, когда миллиарды лет назад испускали свет, который до нас доходит сейчас. Начиная с определенного расстояния мы возвращаемся к эпохе, очень близкой к Большому взрыву, когда первые галактики еще не родились и Вселенная была темной: мы достигаем «космологического горизонта» – границ наблюдаемой Вселенной. Таким образом, мы не можем наблюдать всю Вселенную, будь она конечной или бесконечной, и ночное небо кажется черным.

На самом деле оно не совсем черное, а наполнено электромагнитным излучением гораздо большей длины волны, чем видимый свет (порядка миллиметра вместо микрометра). Это низкочастотное излучение, невидимое для глаз, улавливается достаточно чувствительным радиотелескопом (см. илл.). Его непреднамеренное открытие в 1964 году принесло американцам Арно Пензиасу и Роберту Уилсону Нобелевскую премию по физике в 1978 году. Речь идет о «микроволновом реликтовом излучении», которое излучается не звездами. Из-за расширения Вселенной его длина волны со временем увеличивается.

 

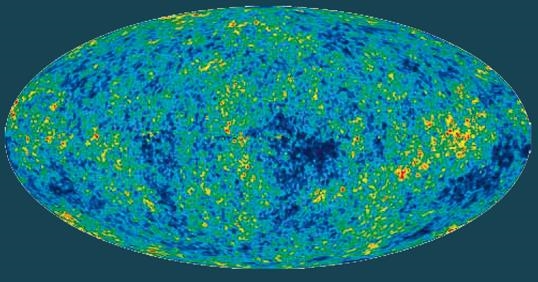
Первая «карта» Вселенной, или микроволновое реликтовое излучение, около 14 миллиардов лет назад. Карта отображает колебания температуры в разных точках Вселенной через 380 000 лет после ее рождения, которые соответствуют местам зарождения будущих галактик. С момента экспериментального подтверждения существования реликтового излучения в 1964 году оно изучается с помощью приборов, установленных на спутниках или в люльках под аэростатами. Приведенная здесь первая детальная карта построена по данным со спутника Wilkinson Microwave Anisotropy Probe

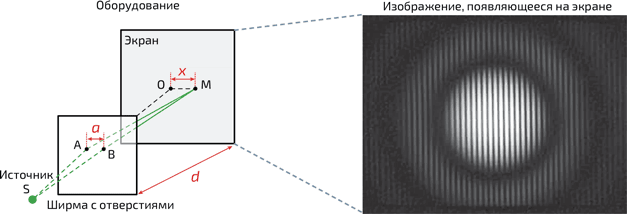
6. Опыт Юнга с интерференцией на отверстиях. Источник монохроматического света направлен на отверстия: на экране наблюдается чередование светлых и темных полос. Лучи, исходящие из A и B, интерферируют. С одним отверстием можно наблюдать размытое пятно, окруженное кольцом из-за явления дифракции

Интерференция и когерентность

Явление интерференции света было доказано в начале XIX века историческим опытом английского физика Томаса Юнга. Ученые той эпохи спорили о природе света: его интерпретировали или как волновое явление, что, казалось, подтвердил опыт Юнга, или как поток частиц. В четвертой части этой книги (см. главу 22) мы увидим, что все они были правы.

Устройство Юнга (илл. 6) содержит точечный источник монохроматического света S, расположенный перед непрозрачной пластиной, в которой на расстоянии нескольких миллиметров друг от друга проделаны два отверстия чрезвычайно малого диаметра (порядка 0,1 мм). Свет, проходящий через отверстия, достигает экрана. И мы видим на нем – удивительно! – не сплошное пятно света, а пятно, демонстрирующее чередование темных и светлых полос. Как так получается?

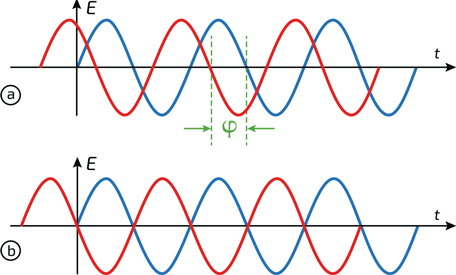
7. a. Две волны с произвольным фазовым сдвигом φ.

b. Две волны в противофазе интерферируют, мешая друг другу: максимальная амплитуда одной соответствует минимальной амплитуде другой

8. Основная (более яркая, справа) и вторичная радуги. Их цвета расположены в противоположном порядке

Интенсивность света, наблюдаемая в точке M экрана, является результатом наложения волн, исходящих из отверстий A и B. Это явление алгебраического суммирования волн, приходящих из разных точек, называется интерференцией. Оно может привести и к нулевой или низкой общей интенсивности (это означает деструктивную интерференцию), и к более высокой интенсивности (так называемая конструктивная интерференция). Конструктивный или деструктивный характер интерференции зависит от смещения волн относительно друг друга, или фазового сдвига, в момент их попадания на экран (илл. 7).

На оси SO волны, исходящие из A и B, находятся в фазе: наблюдается светлая полоса. По мере отклонения от этой оси, в зависимости от точки на экране, волны преодолевают различные расстояния (оптические пути) от отверстий. Их фазы расходятся, и в результате наблюдается периодический ряд светлых и темных полос. Существует деструктивная интерференция (темная полоса), когда разница в длине оптического пути равна половине длины волны, или нечетному числу длин полуволн. Есть и конструктивная интерференция (светлая полоса), когда разница в длине оптического пути кратна длине волны.

Для видимого света длина волны λ – порядка микрометра, что примерно в десять раз меньше диаметра волоса. Однако расстояние между полосами на экране значительно возрастает, если этот экран находится на достаточном расстоянии d от отверстий. Размер OM = x полос может быть найден из условия AM – BM = nλ, где n – целое число. Если a = AB – расстояние между отверстиями, то расстояние между полосами равно λd/a. Приняв λ = 0,5 мкм, d = 3 м и a = 0,5 см, находим, что расстояние между полосами составляет 0,3 мм. Таким образом, становится понятно, почему нам удается увидеть интерференционные полосы невооруженным глазом, хотя это и не всегда просто. При практических работах по интерференции сегодняшние студенты часто сталкиваются с трудностями. Поэтому нам остается лишь восхищаться Юнгом, который сумел поставить этот опыт два века назад.

9. Путь световых лучей в основной и вторичной радугах. Средний угол отклонения – 42° и 51° соответственно. Впоследствии лучи света, составляющие основную радугу, образуют конус вращения, осью которого является прямая «Солнце – наблюдатель», а угол между ней и образующими составляет 42°

А что будет, если вместо освещения двух отверстий одним и тем же источником света использовать два точечных источника монохроматического света? Оказывается, что в этом случае эксперимент потерпит неудачу! Интерференция возможна только для когерентных источников, фазовый сдвиг которых постоянен во времени. Два же случайных источника, если не принять каких-либо особых мер, не удовлетворяют этому условию.

Трудность наблюдения за интерференцией света может навести на мысль, что это довольно экзотическое явление. Вовсе нет! Хорошим примером интерференции служат радужные переливы на мыльных пузырях (см. главу 6, «Мыльные пузыри»). В этом случае интерференция происходит между светом, отраженным от передней и задней границ мыльной пленки. Поскольку наблюдения обычно производятся при белом свете, то волны, находящиеся в противофазе, гасят друг друга, и полученный свет выглядит разноцветным. Видимый цвет пленки зависит от ее толщины и от положения наблюдателя относительно пузыря. Подобные интерференционные переливы цвета можно увидеть на крыльях бабочек, в оперении колибри, а также на наружном покрове некоторых насекомых.

Цвета радуги

Радуга возникает из-за взаимодействия солнечного света с каплями воды, взвешенными в атмосфере (илл. 8). Эти капли размером порядка 0,1 мм значительно больше, чем длина световой волны. В результате путь световых лучей в каждую каплю может быть описан геометрической оптикой, то есть преломлением на входе и на выходе. Между этими преломлениями внутри капли может произойти одно или несколько отражений. Основная радуга, часто единственная видимая, соответствует одному промежуточному отражению, а иногда появляющаяся вторичная радуга создана лучами, которые претерпели два отражения в каплях воды (илл. 9). Для данной длины волны отклонение светового луча каплей воды зависит от того, в какой точке он в нее попадает, и определяется законами преломления. Однако угол между входящим и выходящим из капли лучами не может принимать любое значение. В случае основной радуги он лежит в диапазоне от 0° примерно до 42°, в чем читатель может убедиться, если не боится вычислений. Отклонения, превышающие 42°, допустимы, но максимальная интенсивность достигается в непосредственной близости от 42°. Для вторичной радуги этот угол составляет около 51°. Поворачиваясь к солнцу спиной, мы наблюдаем две яркие дуги. Между ними появляется темный участок: действительно, никакой луч не появится между двумя критическими углами после одного или двух отражений в каплях воды, и потому эта область выглядит темнее, чем остальная часть неба.

Снелл, Декарт и Ферма

Давайте вспомним закон, названный во Франции законом Снелла – Декарта или просто законом Декарта, а в других странах – законом Снеллиуса (см. главу 2, «Отражение и преломление световых волн»). Декарт, по-видимому, первым опубликовал его в трактате «Диоптрика» в 1637 году, но закон уже был открыт голландским математиком Виллебрордом Снеллом, или Снеллиусом (1580–1626), а до него – персидским ученым Ибн Салемом в конце X века.

Снелл, вероятно, основывался на экспериментальных работах, в то время как Декарт утверждал, что открыл этот закон, приравняв луч света к траектории пули. Это не слишком понятное доказательство было раскритиковано Пьером де Ферма в работе, опубликованной в 1662 году под названием «Сумма о преломлениях» (Synthèse pour les réfractions). Принцип Ферма, изложенный в этом тексте, гласит, что свет проходит по пути, который позволяет ему скорейшим образом перейти от точки А к точке В (см. илл.). Предоставим читателю вывести закон Снеллиуса из принципа Ферма, что не составит труда при наличии некоторого знания тригонометрии и дифференциального исчисления. Просто найдите точку C, которая минимизирует время, затраченное светом, чтобы пройти по пути ABC, – это время равно (AC/c) + (BC/v), где c – скорость света в воздухе и v = c/n – его скорость в воде.

Если доказательство Декарта любопытно скорее с исторической стороны, то принцип Ферма сохраняет определенный интерес и для современной физики. Кроме того, именно Декарт первым объяснил появление двух радуг и рассчитал соответствующие углы отклонения.

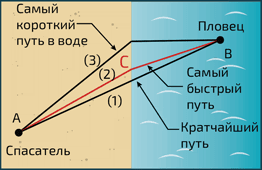
Аналогия с проблемой спасателя

Спасатель (А), которому нужно как можно скорее спасти пловца (B), бежит по пляжу быстрее, чем плывет в море. Самый краткий путь, прямой (1), не будет самым быстрым: спасатель потеряет много времени в море. Если же он максимально сократит время плавания (3), то значительно увеличит путь по пляжу. В итоге самый быстрый путь (2), проходящий через C, – тот, который отвечает закону Снеллиуса

Так объясняется появление световых дуг, но не их цветов… На самом деле точное значение угла отражения зависит от цвета, так как показатель преломления воды n увеличивается, когда длина волны уменьшается. Итак, для фиксированного угла падения i угол преломления увеличивается с длиной волны, то есть двигается от синего к красному. Это значит, что отклонение на входе и выходе капли сильнее для синего, чем для красного. Таким образом, с внешней стороны дуги появляется красный цвет. Все наоборот во вторичной радуге, цвета которой расположены в обратном порядке: красный внутри. Эти вытекающие из геометрии и законов преломления странности – примеры сюрпризов, что порой несут нам научные расчеты.

А птицы?

Рассматривая картину Рылова, мы еще не обсудили птиц, которые составляют неотъемлемую часть обаяния морских берегов. Давайте исправим это упущение такой задачей: как часто птице заданной массы нужно взмахивать крыльями, чтобы лететь? Возможно, читателю трудно будет увидеть связь между этими величинами, и он решит, что авторы играют с ним как кошка с мышкой.

Пусть m – масса птицы, S – общая площадь крыльев, v – средняя скорость крыла, t – продолжительность удара крыла и ρ – плотность воздуха. Во время взмаха крылом птица перемещает воздушную массу, равную M = ρSvt, и сообщает ей скорость v, что соответствует среднему ускорению v/t, поэтому сила F = Mv/t = ρSv² должна сбалансировать вес mg птицы, где g – ускорение свободного падения. Так,

Скорость v крыла пропорциональна количеству взмахов крыльев в секунду υ и длине крыла, которая также пропорциональна 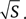Предполагая (довольно произвольно), что коэффициент пропорциональности равен 2π, находим:

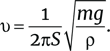
Для серой цапли (илл. 10) масса m составляет порядка 1 кг. Размах ее крыльев – около 2 м, и можно предположить, что площадь S ≈ 0,2 м². При приблизительных значениях ρ = 1 кг/м³ и g = 10 м/с² скорость крыла будет составлять порядка 3 взмахов в секунду, что вполне соответствует реальности между 2 и 3 взмахами в секунду в машущем полете.

10. Площадь крыла серой цапли примерно равна одной десятой квадратного метра

Пойдем дальше и предположим, что все птицы имеют тело той же формы и плотности. Площадь крыльев S в таком случае пропорциональна m^2/3, и из предыдущей формулы следует, что количество взмахов крыльев в секунду обратно пропорционально m^1/6. Действительно, υ уменьшается при увеличении массы птицы: воробей (масса которого составляет порядка 20–30 г) совершает 13 взмахов в секунду, голубь (масса около 500 г) – до 8–9 взмахов, а сарыч (масса примерно килограмм) – до 3.

А насекомые? На картине Рылова их не видно, так как они слишком малы. У насекомых частота взмахов крыла значительно выше, чем у птиц, что соответствует нашей формуле. Предельный случай – комары, которые совершают примерно 400 взмахов в секунду. Ударяя воздух с такой частотой, насекомое производит слышимый человеком звук, чем предупреждает о своих атаках! Зная, что масса комара составляет 2 мг, и предполагая, что крылья имеют площадь поверхности S порядка 10 мм², можно заключить, что фактическая частота примерно в 10 раз выше, чем значение, получаемое по нашей формуле. В этом нет ничего удивительного, формула действительно очень приблизительна, и скорее следует удивляться тому, что она дает разумные значения частот взмахов крыльями для крупных птиц и насекомых.

Мог ли художник Рылов, когда писал свою картину, предполагать, что затронет так много законов физики?