
Иэн Стюарт
Математика космоса: Как современная наука расшифровывает Вселенную
1. Притяжение на расстоянии
Макавити, Макавити, таинственный Макавити!
Законы наши соблюдать его вы не заставите.
Презрел он тяготения всемирного закон.
Томас Стернс Элиот «Учебник Старого Опоссума по котоведению» (Перевод С. Я. Маршака)
Почему предметы падают вниз?
Некоторые не падают. Среди них, очевидно, и Макавити. А также Солнце, Луна и почти все, что есть «там, на небесах». Хотя иногда с неба падают камни, и динозавры, к своему несчастью, убедились в этом. Здесь, на Земле, если уж вы хотите немного попридираться, летают насекомые, птицы и летучие мыши, но они не могут держаться в воздухе вечно. А все остальное неизменно падает – если, конечно, что-то не удерживает его вверху. Но те штуки, которые в небесах, ничто там не удерживает – и все же они не падают.
Кажется, что там, на небесах, все совершенно иначе, чем здесь, на земле.
Потребовалось озарение гения, чтобы понять, что земные объекты падают на Землю под действием той же самой причины, которая удерживает небесные объекты наверху. Ньютон, как широко известно, сравнил падающее яблоко с Луной и понял, что Луна остается наверху, потому что она, в отличие от яблока, движется еще и вбок[8]. На самом деле Луна непрерывно падает, но поверхность Земли уходит от нее с той же скоростью. Так что Луна может падать вечно, но при этом раз за разом огибать Землю, так никогда на нее и не упав.
Настоящая разница заключается не в том, что яблоки падают, а Луны – нет. Разница в том, что яблоки не движутся вбок достаточно быстро, чтобы пролететь мимо Земли.
Ньютон был математиком (а также физиком, химиком и мистиком), так что он немного посчитал, чтобы подтвердить свою радикальную мысль. Вычислил силы, которые должны действовать на яблоко и на Луну, чтобы те двигались по своим разным маршрутам. С учетом различия в массах этих объектов силы оказались одинаковыми. Это убедило Ньютона в том, что Земля, должно быть, притягивает к себе и яблоко, и Луну. Было естественно предположить, что притяжение того же типа действует в любой паре объектов: хоть земных, хоть небесных. Ньютон выразил эти силы притяжения математическим уравнением, сформулировав закон природы.
Одно из замечательных следствий из этого закона состоит в том, что не только Земля притягивает яблоко: яблоко тоже притягивает Землю. И Луну, и все остальные объекты во Вселенной. Но действие яблока на Землю слишком мало, чтобы его можно было измерить, в отличие от действия Земли на яблоко.
Это открытие стало гигантским успехом, глубоким и отчетливым связующим звеном между математикой и миром природы. У него есть и еще одно важное следствие, которое легко пропустить среди математических терминов и деталей: невзирая на внешнее несходство, «там, на небесах» в некоторых жизненно важных отношениях все обстоит точно так же, как «здесь, на земле». Законы там и там действуют одинаковые. Различается только контекст их приложения.
Мы называем загадочную Ньютонову силу гравитацией или тяготением. Мы умеем рассчитывать ее действие с величайшей точностью. И мы по-прежнему не понимаем ее.
* * *
Долгое время нам казалось, что мы ее понимаем. Около 350 года до нашей эры греческий философ Аристотель дал простое объяснение тому, что все предметы падают вниз: они просто стремятся к своему естественному местоположению.
Чтобы избежать в рассуждениях замкнутого круга, он объяснил также, что значит «естественный». Аристотель полагал, что все на свете состоит из четырех базовых элементов: земли, воды, воздуха и огня. Естественное местоположение земли и воды находится в центре Вселенной, который, разумеется, совпадает с центром Земли. Это доказывается тем, что Земля не движется: мы живем на ней и, конечно, заметили бы, если бы она двигалась. Поскольку земля тяжелее воды (она ведь тонет, верно?), самые нижние уровни заняты землей и представляют собой шар. Далее идет сферическая оболочка из воды, затем – тоже сферическая оболочка из воздуха (воздух легче воды: пузырьки воздуха всплывают). Выше воздуха, но ниже небесной сферы, несущей на себе Луну, располагается царство огня. Все остальные тела имеют тенденцию подниматься или падать в зависимости от соотношения в них этих четырех элементов.
Эта теория привела Аристотеля к утверждению о том, что скорость падающего тела пропорциональна его весу (перья падают медленнее, чем камни) и обратно пропорциональна плотности окружающей среды (камни быстрее падают в воздухе, чем в воде). Достигнув своего естественного местоположения, тело остается там и двигается лишь при приложении некоторой силы.
Как теория эта точка зрения не так уж плоха. В частности, она вполне соответствует повседневному опыту. Сейчас, когда я пишу эту книгу, на моем столе лежит первое издание романа «Трипланетие» (Triplanetary), который цитируется в эпиграфе ко второй главе. Если я не буду его трогать, то книга останется на месте и будет спокойно лежать. Если я приложу силу – скажем, толкну эту книгу, – то она сдвинется на несколько сантиметров, замедляясь по ходу движения, и остановится.
Аристотель прав.
Так все и выглядело на протяжении почти двух тысяч лет. Аристотелева физика, несмотря на множество возражений, в целом принималась практически всеми интеллектуалами до конца XVI столетия. Исключением был арабский ученый аль-Хасан ибн аль-Хайсам (Альхазен), который в XI веке выступал против воззрений Аристотеля из геометрических соображений. Но даже сегодня Аристотелева физика точнее отвечает нашим интуитивным представлениям, чем пришедшие ей на смену идеи Галилея и Ньютона.
С современной точки зрения в теории Аристотеля есть несколько крупных пробелов. Один из них – вес. Почему перо легче камня? Еще один пробел – трение. Предположим, я положил бы мой экземпляр «Трипланетия» на лед катка и дал ему такой же толчок. Что произошло бы? Книга уехала бы дальше – и еще дальше, если бы я приладил к ней коньки. Трение заставляет тело двигаться медленнее в вязкой – клейкой – среде. Трение в повседневной жизни встречается на каждом шагу, и именно поэтому Аристотелева физика лучше отвечает нашим интуитивным представлениям, чем Галилеева и Ньютонова физика. В процессе эволюции наш мозг выработал внутреннюю модель движения, в которую уже встроено трение.
Сегодня мы знаем, что тело падает на Землю потому, что притягивается земным тяготением. Но что такое тяготение? Ньютон считал тяготение силой, но не объяснял, откуда эта сила берется и как возникает. Она просто есть. Она действует на расстоянии без всяких посредников. Как это происходит, он тоже не объясняет; она просто действует. Эйнштейн заменил силу кривизной пространства-времени, сделав «действие на расстоянии» излишним, и записал в виде уравнений, как на эту кривизну влияет распределение вещества в пространстве, но и он не объяснил, почему кривизна ведет себя таким образом.
Человек научился рассчитывать некоторые аспекты космоса, к примеру вычислять времена затмений, за тысячи лет до того, как кто-либо понял, что гравитация существует. Но после того как роль гравитации была раскрыта, наши возможности в области космических вычислений многократно выросли. Третьей книге своих «Начал», в которой описывались законы движения и гравитации, Ньютон дал подзаголовок «О системе мира». Это было всего лишь небольшое преувеличение. Сила тяготения и то, как тела реагируют на силы, лежит в основе большинства космических вычислений. Поэтому, прежде чем мы перейдем к новейшим открытиям и поговорим, к примеру, о начале Вселенной или о том, как планеты, обладающие кольцами, порождают новые луны, нам полезно будет разобраться в некоторых базовых представлениях, связанных с гравитацией.
* * *
До изобретения уличного освещения Луна и звезды были так же хорошо знакомы большинству людей, как и близлежащие реки, деревья и горы. Когда заходило Солнце, появлялись звезды. Луна двигалась в собственном ритме и по собственному расписанию, иногда она появлялась в небесах среди бела дня и выглядела как бледный призрак, но по ночам светила намного ярче. Тем не менее закономерности в ее движении тоже присутствовали. Всякий, кто наблюдал бы Луну хотя бы между делом на протяжении нескольких месяцев, скоро заметил бы, что она следует регулярному ритму и каждые 29 дней меняет форму с тонкого полумесяца до полного диска и обратно. Кроме того, она заметно сдвигается от ночи к ночи, проходя по небу одним и тем же повторяющимся из раза в раз замкнутым маршрутом.
У звезд также есть собственный ритм. Один раз в сутки они обходят вокруг некоторой фиксированной точки в небесах, как будто они нарисованы на внутренней стороне медленно вращающейся чаши. В книге «Бытие» говорится о небесной тверди; в переводе с еврейского «твердь» означает «чаша».
Если наблюдать небо на протяжении нескольких месяцев, становится очевидным также, что пять звезд, включая некоторые из самых ярких на небе, не вращаются подобно большинству «фиксированных», или неподвижных, звезд. Они не закреплены на чаше, а медленно ползут по ней. Греки связывали эти блуждающие световые точки с Гермесом (посланцем богов), Афродитой (богиней любви), Аресом (богом войны), Зевсом (царем всех богов) и Кроносом (богом земледелия). Соответствующие римские божества дали им их нынешние названия: Меркурий, Венера, Марс, Юпитер и Сатурн. Греки назвали эти блуждающие звезды planetes, то есть «странники», отсюда произошло современное слово «планеты». Сегодня мы знаем еще три планеты: это сама Земля, Уран и Нептун. Пути планет на небе выглядели странно и казались непредсказуемыми. Некоторые из них двигались относительно быстро, другие медленнее. Некоторые даже возвращались по своим следам и за несколько месяцев описывали на небе замкнутую петлю.
В большинстве своем люди просто принимали окружающую их действительность такой, какая она есть, точно так же, как принимали существование рек, деревьев и гор и считали небесные огоньки небесными огоньками. Но некоторые задавали вопросы: что представляют собой эти огоньки? Откуда они на небе? Как и почему они движутся? Почему одни огоньки движутся по правилам, а другие их нарушают?
Шумеры и вавилоняне собрали основные наблюдательные данные. Они записывали их на глиняных табличках так называемой клинописью – особыми знаками, напоминающими по форме клин. Среди найденных археологами вавилонских табличек имеются звездные каталоги, где записано положение звезд на небе; они датируются приблизительно 1200 годом до нашей эры, но, вероятно, являются копиями еще более ранних шумерских табличек. Греческие философы и геометры, продолжавшие дело шумеров и вавилонян, лучше своих предшественников сознавали необходимость логики, доказательств и теории. Они во всем искали закономерности; последователи пифагорейского культа довели этот принцип до крайности: они верили, что Вселенной правят числа. Сегодня большинство ученых согласились бы с ними, но не в деталях.
Наибольшее влияние на астрономическое мышление позднейших поколений оказал Клавдий Птолемей – греческий геометр, астроном и географ. Его самая ранняя работа известна как «Альмагест» – по арабскому сокращению оригинального названия, которое сперва звучало как «Математическое собрание», затем превратилось в «Великое собрание», а затем в просто в al-majisti – «величайшее». В «Альмагесте» была представлена законченная теория планетарного движения, основанная на наиболее совершенных, по мнению греков, геометрических фигурах – окружностях и сферах.
На самом деле планеты движутся не по окружностям. Это заявление не удивило бы вавилонян, потому что движение по окружностям не соответствовало их таблицам. Греки пошли дальше и задались вопросом: а что же им соответствует? Ответ Птолемея был таков: сочетания окружностей, поддерживаемых сферами. Внутренняя сфера – «деферент» – строится вокруг Земли, которая и является ее центром. Ось второй сферы – «эпицикла» – закреплена слегка внутри первой. Каждая пара сфер самостоятельна и не связана с остальными. Идея сама по себе не новая. Двумя столетиями ранее Аристотель, опираясь на еще более ранние идеи того же рода, предложил сложную систему из 55 концентрических сфер, в которой ось каждой сферы закреплена на ближайшей к ней внутренней сфере. В модификации Птолемея сфер было меньше, да и система работала точнее, но по-прежнему оставалась довольно сложной. И обе системы заставляли думать о том, существуют ли все эти сферы в реальности, или являются просто удобной выдумкой, или на самом деле происходит что-то совершенно иное.
* * *
Следующую тысячу лет, а то и больше, Европа все свое внимание посвящала вопросам теологическим и философским, а представления о мире природы черпала в основном из трудов Аристотеля, созданных примерно за 350 лет до Рождества Христова. Вселенная считалась геоцентрической, и все в ней вращалось вокруг неподвижной Земли. Факел исследований в астрономии и математике переместился в арабский мир, в Индию и Китай. Однако с зарей итальянского Возрождения этот факел вновь был передан в Европу. После этого ведущие роли в развитии астрономического знания сыграли три гиганта науки: Галилей, Кеплер и Ньютон, а группа поддержки у них была поистине громадной.
Галилей знаменит тем, что усовершенствовал телескоп и обнаружил с его помощью, что на Солнце есть пятна, у Юпитера есть (по крайней мере) четыре луны, Венера проходит такие же фазы, как Луна, а Сатурн выглядит как-то странно – позже странности его внешнего вида получили объяснения в виде системы колец. Полученные данные заставили его отвергнуть геоцентрическую теорию и принять соперничающую с ней гелиоцентрическую теорию Николая Коперника, в которой планеты и Земля вращаются вокруг Солнца; из-за этого у Галилея возникли проблемы с римско-католической церковью. Но он также сделал на первый взгляд более скромное, но в конечном итоге более важное открытие: открыл математическую закономерность в движении таких объектов, как пушечные ядра. Здесь, на Земле, свободно движущееся тело либо ускоряется (при падении), либо замедляется (при подъеме) на величину, одинаковую за фиксированный, небольшой отрезок времени. Короче говоря, ускорение тела постоянно. Поскольку точных часов в его распоряжении не было, Галилей наблюдал эти эффекты, катая шары по слегка наклонным желобам.
Еще одна ключевая фигура того времени – Кеплер. Его учитель и начальник Тихо Браге в свое время провел очень точные измерения положения Марса. После смерти Тихо Кеплер унаследовал не только его положение придворного астронома при императоре Священной Римской империи Рудольфе II, но и продолжил наблюдения и занялся вычислением точной формы орбиты Марса. После 50 неудачных попыток он рассчитал, что орбита имеет форму эллипса, то есть овала, напоминающего слегка сплюснутую окружность. При этом Солнце находится в особой точке этого эллипса – в его фокусе.
Древнегреческие геометры знали эллипсы и определяли их как сечение конуса плоскостью. В зависимости от наклона плоскости относительно оси конуса «конические сечения» включают в себя окружности, эллипсы, параболы и гиперболы.
Когда планета движется по эллипсу, расстояние от нее до Солнца меняется. Приближаясь к Солнцу, планета ускоряется; удаляясь от Солнца, замедляется. Немного удивительно, что все эти эффекты в сумме умудряются создать орбиту в точности одинаковую по форме с обеих сторон. Кеплер этого не ожидал, и его долгое время преследовала мысль, что эллипс в ответе, должно быть, получился по ошибке.
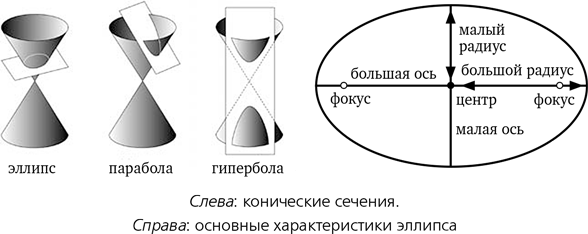
Форма и размер эллипса определяются двумя длинами: длиной большой оси, представляющей собой самый длинный отрезок прямой, соединяющий две точки на эллипсе, и длиной малой оси, которая перпендикулярна большой. Окружность – это разновидность эллипса, для которой две указанные длины равны; в этом случае они обе равны диаметру окружности. В астрономии радиус считается более удобной мерой. Так, радиус круговой орбиты равен расстоянию от планеты до Солнца и соответствующие величины для эллипса называют большим радиусом и малым радиусом. К этим же величинам относятся более громоздкие термины «большая полуось» и «малая полуось», поскольку они представляют собой половинки большой и малой оси. Менее интуитивно понятна, но очень важна еще одна характеристика эллипса: его эксцентриситет – это количественное отражение формы эллипса, того, насколько он длинный и тонкий. Эксцентриситет окружности равен нулю, а для фиксированной длины большой полуоси он стремится к единице, по мере того как длина малой полуоси стремится к нулю[9].
Размер и форму эллиптической орбиты можно охарактеризовать двумя числами. Как правило, выбирают большую полуось и эксцентриситет. Малую полуось можно вычислить исходя из этих двух параметров. Большая полуось орбиты Земли составляет 149,6 миллиона километров, ее эксцентриситет равен 0,0167; при этом малая полуось равняется 149,58 миллиона километров, так что орбита очень близка к круговой, на что указывает и малый эксцентриситет. Плоскость земной орбиты имеет особое название – эклиптика.
Пространственное положение любой другой эллиптической орбиты вокруг Солнца можно охарактеризовать тремя дополнительными числами; все три – угловые величины. Одна из этих величин представляет собой наклон орбитальной плоскости к плоскости эклиптики. Вторая величина, по существу, дает направление большой оси орбиты в этой плоскости. Третья дает направление прямой, по которой пересекаются эти две плоскости. Наконец, нам нужно знать, где именно на орбите в данный момент располагается планета, для чего потребуется еще один угол. Таким образом, для того, чтобы определить орбиту планеты и ее положение на этой орбите, нам требуется два числа и четыре угла – шесть орбитальных элементов. Главной целью ранней астрономии было вычислить орбитальные элементы каждой планеты и каждого астероида, которые удалось обнаружить. Имея эти числа, можно предсказывать будущее положение объекта, по крайней мере до тех пор, пока совместное воздействие других тел не приведет к существенному возмущению орбиты.
Со временем Кеплер смог сформулировать набор из трех элегантных математических закономерностей, которые в настоящее время называются законами планетарного движения. Первый из них гласит, что орбита любой планеты представляет собой эллипс, в одном из фокусов которого находится Солнце. Второй – что отрезок прямой, соединяющий Солнце с планетой, за равные промежутки времени заметает равные площади. А третий говорит нам, что квадрат периода обращения пропорционален кубу расстояния.
* * *
Ньютон переформулировал наблюдения Галилея о свободно движущихся телах в виде трех законов движения. Первый из них утверждает, что тело, если на него не действует никакая сила, продолжает двигаться по прямой с постоянной скоростью. Второй гласит, что ускорение любого тела равняется действующей на него силе, отнесенной к массе тела. Третий говорит о том, что всякое действие порождает равное по величине и противоположное по направлению противодействие. В 1687 году Ньютон переформулировал и планетарные законы Кеплера, предложив общее правило, согласно которому движутся небесные тела, – закон всемирного тяготения, математическую формулу для силы, с которой произвольное тело притягивает любое другое тело.
В действительности он вывел свою формулу силы из законов Кеплера, сделав одно допущение: Солнце притягивает к себе планеты с силой, всегда направленной к его центру. Исходя из этого допущения, Ньютон доказал, что сила эта обратно пропорциональна квадрату расстояния. Таким замысловатым образом математики выражают ту мысль, что, к примеру, умножение массы любого из тел на три утраивает также и действующую силу, а вот умножение на три расстояния между объектами снижает силу притяжения между ними до 1/9 первоначального значения. Ньютон доказал также обратное утверждение: из «закона обратных квадратов» следуют три закона Кеплера.
Слава открывателя закона всемирного тяготения справедливо досталась Ньютону, но идея, по существу, была неоригинальна. Кеплер вывел нечто подобное по аналогии со светом, но он полагал, что гравитация толкает планеты в их движении по орбитам. Исмаэль Буйо (подписывавшийся также латинизированным именем Буллиальд) был с ним не согласен; он утверждал, что сила притяжения должна быть обратно пропорциональна квадрату расстояния. Роберт Гук в лекции, прочитанной в Королевском обществе в 1666 году, сказал, что все тела движутся прямолинейно, если на них не действует сила, все тела тяготеют друг к другу и что сила гравитационного притяжения убывает с расстоянием по формуле, которую «я, признаю, еще не установил». В 1679 году Гук пришел к выводу о том, что сила тяготения изменяется с расстоянием по обратно-квадратичному закону, и написал об этом Ньютону. Так что Гук, конечно, был уязвлен, когда обнаружил в точности то же самое в Ньютоновых «Началах», несмотря на то что Ньютон в книге выразил ему благодарность наряду с Галлеем и Кристофером Реном.
Гук, правда, признал, что только Ньютон сумел определить, что замкнутые орбиты имеют форму эллипса. Ньютон знал, что обратно-квадратичная зависимость допускает также параболические и гиперболические орбиты, но эти кривые не являются замкнутыми, так что движение по ним не повторяется периодически. Орбиты такого рода также находят применение в астрономии, в основном там, где речь идет о кометах.
Закон Ньютона превосходил законы Кеплера благодаря одной дополнительной черте, которая была предсказанием, а не теоремой. Ньютон понял, что, поскольку Земля притягивает Луну, разумно предположить, что и Луна, в свою очередь, притягивает Землю. Земля и Луна, как два сельских танцора, держась за руки, кружатся в бесконечном танце. Каждый танцор чувствует, с какой силой партнер тянет его за руки. Каждый танцор удерживается на месте посредством этой силы: если разжать руки, танцоры, кружась, унесутся по залу в разные стороны. Однако Земля намного массивнее Луны, так что процесс напоминает танец толстяка с маленьким ребенком. При этом кажется, что толстяк кружится на месте, а ребенок носится вокруг него кругами. Но посмотрите внимательно, и вы увидите, что толстяк тоже описывает круги: его ноги движутся по небольшому кругу, а центр, вокруг которого он вращается, расположен немного ближе к ребенку, чем должно было бы быть, если бы он вращался один.
Такие рассуждения привели Ньютона к предположению о том, что каждое тело во Вселенной притягивает к себе все остальные тела. Законы Кеплера приложимы только к двум телам – Солнцу и планете. Закон Ньютона применим к любой системе тел в принципе, поскольку он дает как величину, так и направление всех возникающих в системе сил. При подстановке в законы движения комбинация всех этих сил определяет ускорение каждого тела и, следовательно, его скорость и положение в любой момент времени. Провозглашение универсального закона гравитации стало эпохальным событием в истории науки – событием, которое позволило прояснить скрытый математический механизм, обеспечивающий существование Вселенной.
* * *
Ньютоновы законы движения и гравитации положили начало долговременному союзу между астрономией и математикой – союзу, которому мы обязаны значительной частью того, что знаем сегодня о космосе. Но даже если вы поняли, что представляют собой эти законы, то это не значит, что вы сможете напрямую применить их к решению конкретных задач. Сила тяготения, к примеру, нелинейна – этот технический термин означает, в сущности, что вы не можете решать уравнения движения при помощи красивых формул. И при помощи некрасивых, кстати говоря, тоже.
Математики постньютоновской эпохи обходили это препятствие двумя способами: либо разбирали совершенно искусственные (хотя и очень интересные) задачи, такие, например, как взаимодействие трех одинаковых масс, расположенных в вершинах равностороннего треугольника, либо искали приближенные решения более реалистичных задач. Второй подход более практичен, но следует отметить, что немало полезных идей удалось извлечь именно из первого подхода, несмотря на всю его искусственность.
На протяжении долгого времени научным наследникам Ньютона приходилось производить все вычисления вручную – и во многих случаях это была поистине героическая задача. Яркий пример такого рода – Шарль-Эжен Делоне, который в 1846 году начал вычислять приближенную формулу движения Луны. На это у него ушло более двадцати лет, а результаты пришлось публиковать в двух томах. В каждом из этих томов более 900 страниц, и весь второй том занимает собственно формула. В конце XX века результат Делоне удалось проверить с применением компьютерной алгебры (программных систем, способных манипулировать не только числами, но и формулами). Было выявлено всего две небольшие ошибки, одна из которых является следствием другой; суммарный эффект от обеих ошибок пренебрежимо мал.
Законы движения и гравитации – это законы особого рода, законы, выражаемые так называемыми дифференциальными уравнениями. Такие уравнения задают скорость, с которой те или иные величины изменяются с течением времени. Скорость – это быстрота изменения положения тела; ускорение – это быстрота изменения скорости. Знание скорости, с которой в настоящее время изменяется та или иная величина, позволяет вам спроецировать эту величину в будущее. Если машина едет со скоростью 10 метров в секунду, то через секунду она сдвинется на 10 метров. Однако для того, чтобы считать таким способом, нужно, чтобы скорость была постоянной. Если же машина ускоряется, то за секунду она отъедет от вас более чем на 10 метров. Чтобы обойти эту проблему, в дифференциальных уравнениях указывается мгновенная быстрота изменения. По существу, они работают с очень короткими промежутками времени, так что быстроту изменения на этом промежутке можно считать постоянной. На самом деле математикам потребовалось несколько столетий, чтобы довести эту идею до полной логической строгости, поскольку никакой конечный интервал времени нельзя считать мгновенным, если он не равен нулю, а за нулевой интервал времени ничто не меняется.
Компьютеры произвели в этом деле настоящую методологическую революцию. Вместо расчета приближенных формул движения, а затем подстановки чисел в эти формулы теперь можно с самого начала работать с числами. Предположим, вы хотите предсказать, где некоторая система тел – скажем, спутники Юпитера – будет находиться через сто лет. Начните с первоначальных позиций и параметров движения Юпитера, его спутников и всех остальных тел, которые могут иметь значение, – в данном случае это Солнце и Сатурн. Затем, постепенно, один крошечный временной шаг за другим, вычисляйте, как изменяются числа, описывающие все задействованные тела. Повторяйте это действие до тех пор, пока не дойдете до временной отметки сто лет. Стоп. Человек, проводящий вычисления при помощи карандаша и бумаги, не смог бы воспользоваться этим методом для расчета сколько-нибудь реалистичной задачи. На это потребовалось бы несколько жизней. Однако при наличии быстрого компьютера метод становится вполне реализуемым, а современные компьютеры очень и очень быстры.
Откровенно говоря, все не настолько просто. Притом что ошибка на каждом шаге (вызванная тем, что мы считаем быстроту изменений постоянной, хотя на самом деле она успевает немного измениться) очень мала, шагов вам придется сделать ужасно много. При многократных операциях с маленькой ошибкой на каждом шагу результирующая ошибка не обязательно получится маленькой, но тщательно продуманные методы позволяют удержать ошибки под контролем. Именно на это нацелена целая область математики, известная как численный анализ. Удобно называть такие методы «моделированием», что отражает принципиальную роль в них компьютера. Важно понимать, что невозможно решить задачу, просто «засунув ее в компьютер». Кто-то должен запрограммировать машину, задать ей математические правила, которые обеспечат близость вычислительных результатов к реальности.
Правила, о которых идет речь, настолько точны, что астрономы могут предсказывать затмения Солнца и Луны с точностью до секунды, а положение планеты с точностью до нескольких километров на сотни лет вперед. Подобные «предсказательные» расчеты можно проводить и назад во времени, чтобы можно было точно определить, когда и где произошли известные нам по историческим хроникам затмения. Эти данные используются, к примеру, для датирования наблюдений, сделанных тысячи лет назад китайскими астрономами.
* * *
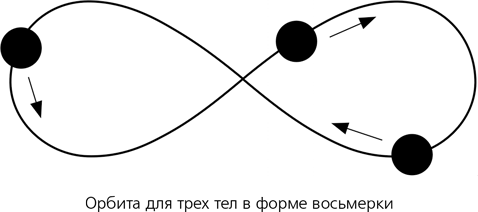
Даже сегодня математики и физики продолжают открывать новые неожиданные следствия из закона всемирного тяготения Ньютона. В 1993 году Крис Мур при помощи численных методов показал, что три тела с идентичными массами могут вечно гоняться друг за другом по одной и той же орбите в форме восьмерки, а в 2000-м Карлес Симо также численно показал, что эта орбита стабильна с точностью, возможно, до медленного дрейфа. В 2001 году Ален Ченсинер и Ричард Монтгомери привели строгое доказательство существования такой орбиты на основе принципа наименьшего действия – фундаментальной теоремы классической механики. Симо открыл множество подобных «хореографий», в которых несколько тел одинаковой массы преследуют друг друга, двигаясь все время по одному и тому же (сложному) пути.
Орбита в форме восьмерки для трех тел, судя по всему, сохраняет стабильность и при слегка различных массах тел, что открывает небольшую вероятность того, что где-то во Вселенной три реальные звезды могут вести себя таким замечательным образом. Согласно оценкам Дугласа Хегги, по одной такой тройной системе может приходиться на каждую галактику, а уж вероятность существования во Вселенной хотя бы одной такой системы довольно значительна.
Все эти орбиты существуют на плоскости, но есть уже и новый трехмерный вариант. В 2015 году Юджин Окс догадался, что необычные орбиты электронов в «ридберговских квазимолекулах», возможно, тоже существуют по законам Ньютоновой гравитации. Он показал, что в системах двойных звезд могут существовать планеты, двигающиеся от одной звезды к другой и обратно по спиральной орбите, обвивающей соединяющую эти звезды линию. В середине витки спирали лежат свободнее, к звездам на концах – плотнее. Представьте себе, что вы протягиваете между звездами пружинку игрушку-слинки, растянутую посередине и свернутую в петли на концах. Для звезд с разными массами пружинка должна сужаться от одного конца к другому, как конус. Подобные орбиты могут быть стабильными, даже если звезды движутся не по окружностям.



