Youri Veniaminovich Kraskov
The Wonders of Arithmetic from Pierre Simon de Fermat

3.2.3. Basic Properties of Numbers

The consequence to the axioms of actions are the following basic properties of numbers due to the need for practical calculations:

1. Filling: a+1>a

2. The neutrality of the unit: a×1=a:1=a

3. Commutativity: a+b=b+a; ab=ba

4. Associativity: (a+b)+c=a+(b+c); (ab)c=a(bc)

5. Distributivity: (a+b)c=ac+bc

6. Conjugation: a=c → a±b=b±c; ab=bc; a:b=c:b; ab=cb; log_ba=log_bc

These properties have long been known as the basics of primary school and so far, they have been perceived as elementary and obvious. The lack of a proper understanding of the origin of these properties from the essence the notion of number has led to the destruction of science as a holistic system of knowledge, which must now be rebuilt beginning from the basics and preserving herewith everything valuable that remains from real science.

The presented above axiomatics proceeds from the definition the essence the notion of number and therefore represents a single whole. However, this is not enough to protect science from another misfortune i.e. so that in the process of development it does not drown in the ocean of its own researches or does not get entangled in the complex interweaving of a great plurality of different ideas.

In this sense, it must be very clearly understood that axioms are not statements accepted without proof. Unlike theorems, they are only statements and limitations synthesized from the experience of computing, without of which they simply cannot be dispensed. Another meaning is in the basic theorems, which are close to axioms, but provable. One of them is the Basic or Fundamental theorem of arithmetic. This is such an important theorem that its proof must be as reliable as possible, otherwise the consequences may be unpredictable.

Pic. 33. Initial Numbers Pyramids

3.3. The Basic Theorem of Arithmetic

3.3.1. Mistakes of the Greats and the Fermat's Letter-Testament

The earliest known version of the theorem is given in the Euclid's "Elements" Book IX, Proposition 14.

If a number be the least that is measured by prime numbers, it will not be measured by any other prime number except those originally measuring it.

The explain is following: “Let the number A be the least measured by the prime numbers B, C, D. I say that A will not be measured by any other prime number except B, C, D”. The proof of this theorem looks convincing only at first glance and this visibility of solidity is strengthened by a chain of references: IX-14 → VII-30 → VII-20 → VII-4 → VII-2.

However, an elementary and even very gross mistake was made here. Its essence is as follows:

Let A=BCD where the numbers B, C, D are primes. If we now assume the existence of a prime E different from B, C, D and such that A=EI then we conclude that in this case A=BCD is not divisible by E.

This last statement is not true because the theorem has not yet been proven and it doesn’t exclude for example, BCD=EFGH where E, F, G, H are primes other than B, C, D. Then

A:E=BCD:E=EFGH:E=FGH

i.e. in this case it becomes possible that the number A can be divided by the number E and then the proof of the theorem is based on an argument that has not yet been proven, therefore, the final conclusion is wrong. The same error can take place also in other theorems using decomposition of integers into prime factors. Apparently, due to the archaic vocabulary Euclid's “Elements” even such a great scientist as Euler did not pay due attention to this theorem, otherwise, he would hardly have begun to use “complex numbers” in practice that are not subordinate to it.

The same story happened with Gauss who also did not notice this theorem in the Euclid's "Elements", but nevertheless, formulated it when a need arose. The formulation and proof of Gauss are follows:

“Each compose number can be decomposed into prime factors in a one only way.

If we assume that a composite number A equal to a^αb^βc^γ …, where a, b, c, … denote different primes, can be decomposed into prime factors in another way, then it is first of all clear that in this second system of factors, there cannot be other primes except a, b, c, …, because the number A composed of these latter cannot be divisible by any other prime number” [11, 25].

This is an almost exact repeating of erroneous argument in the Euclid's proof. But if this theorem is not proven, then the whole foundation of science built on natural numbers collapses and all the consequences of the definitions and axioms lose their significance. And what to do now? If such giants of science as Euclid and Gauss could not cope with the proof of this theorem, then what we sinners can to do. But yet there is a way out and it is indicated in one amazing document called "Fermat's Letter-Testament".

This letter was sent by Fermat in August 1659 to his longtime friend and former colleague in the Parliament of Toulouse the royal librarian Pierre de Carcavy from whom he was received by the famous French scientist Christian Huygens who was the first to head the French Academy of Sciences created in 1666. Here we give only some excerpts from this Fermat's letter, which are of particular interest to us [9, 36].

“Summary of discoveries in the science about numbers. …

1. Since the usual methods set in the Books are not sufficient to prove very difficult sentences, I finally found a completely special way to solve them. I called this method of proof infinite or indefinite descent. At first, I used it only to prove negative sentences such as: … that there exists no a right triangle in numbers whose area is a square”. See Appendix II for details.

The science about numbers is called here arithmetic and the further content of the letter leaves no doubt about it. Namely with arithmetic not only mathematical, but also all other sciences begin. In arithmetic itself the descent method is one of the fundamental one. The following are examples of problems whose solution without this method is not only very difficult, but sometimes even hardly to be possible. Here we will name only a few of these examples.

"2. For a long time, I could not apply my method to affirmative sentences because rounds and circuitous ways to achieve the aim are much more difficult than those that served me for negative sentences. Therefore, when I needed to prove that every prime number that is by unit more than multiple of four, consists of <sum of> two squares, I was in a greatest difficulty. But finally, my thoughts repeated many times shed light that I did not have and the affirmative sentence became possible to interpret with my method using some new principles that needed to be attached to them. This progress in my reasoning for the case of affirmative sentences is as follows: if some prime number that on 1 exceeds the multiplied of 4, does not consist of two squares, then there is another a prime number of the same nature, smaller than this and then a third, also smaller etc. going down until you come to the number 5, which is the smallest from all numbers of this nature. It therefore, cannot consist of two squares, what however, takes place. From this by proof from the contrary we can conclude that all primes of this nature should consist of two squares”.

This Fermat’s theorem was first proven by Euler in 1760 [6, 38], (see Appendix III), and in the framework of the very complex Gauss' "Deductive Arithmetic" this theorem is proving in one sentence [23]. However, no one succeeded in repeating the proof of Fermat himself.

“… 3. There are infinitely many questions of this kind, but there are others that require new principles for applying the descent method to them … This is the next question that Bachet as he confesses in his commentary on Diophantus, could not prove. On this occasion, Descartes made the same statement in his letters acknowledging that he considers it so difficult that he sees no way to solve it. Each number is a square or consists of two, three or four squares".

Else earlier, 22 years ago, in October 1636 in a letter to Mersenne Fermat reported on the same problem as about his discovery, but in general form i.e. for any polygonal numbers (for example, triangles, squares, pentagons etc.). Subsequently, he even called this theorem golden one. Consequently, the method of descent was discovered by him at the very beginning of his research on arithmetic. By the time of writing the letter-testament, Fermat already knew from Carcavy that the question of foundation the French Academy of Sciences was practically resolved and he needed only to wait for the building to be completed, so it come true his life's dream to become a professional scientist in the rank of academician. Huygens was commissioned to collect materials for the first academic publications. Fermat proposed for them the method of descent discovered by him and the solution of specific arithmetic tasks on its basis.

However, only few people knew that these tasks were very difficult and Fermat understood that if he would publish their solutions, they would not make any impression at all. He already had such an experience and now he has prepared a real surprise. For those who don't appreciate the value of his solution, he would offer to solve another task. This is the Basic theorem of arithmetic, which is of particular importance for all science since without it the whole theory loses its strength. Fermat found a mistake in the proof of Euclid and came to the conclusion that to prove this theorem without applying the descent method is extremely difficult if at all possible. However, now we can also reveal this secret with the help of our opportunities to look into Fermat’s cache with “heretical writings” and return his lost proof to science in the form of the reconstruction presented below.

3.3.2. The Proof of Fermat

So, to prove the Basic theorem of arithmetic we suppose that there exist equal natural numbers A, B consisting of different prime factors:

A=B (1)

where A=pp₁p₂ …p_n; B=хx₁x₂ …x_m ; n≥1; m≥1

Due to the equality of the numbers A, B each of them is divided into any of the prime numbers p_i or x_i. Each of the numbers A, B can consist of any set of prime factors including the same ones, but at the same time there is no one p_i equal to x_i among them, otherwise they would be in (1) reduced. Now (1) can be represented as:

pQ=xY (2)

where p, x are the minimal primes among p_i, x_i; Q=A/p; Y=B/x .

Since the factors p and x are different, we agree that p>x; x=p–δ₁ then

pQ=(p – δ₁)(Q+δ₂) (3)

where δ₁=p–x; δ₂=Y–Q

From (3) it follows that Qδ₁=(p – δ₁)δ₂ or

Qδ₁=xδ₂ (4)

Equation (4) is a direct consequence of assumption (1). The right side of this equation explicitly contains the prime factor x. However, on the left side of equation (4) the number δ₁ cannot contain the factor x because δ₁ = p – x is not divisible by x due to p is a prime. The number Q also does not contain the factor x because by our assumption it consists of factors p_i among which there is not a single equal to x. Thus, there is a factor x on the right in equation (4), but not on the left. Nevertheless, there is no reason to argue that this is impossible because we initially assume the existence of equal numbers with different prime factors.

Then it remains only to admit that if there exist natural numbers A = B composed of different prime factors, then it is necessary that in this case there exist another natural number A₁=Qδ₁ and B₁=xδ₂; also equal to each other and made up of different prime factors. Given that δ₁=(p–x)<p, and δ₂=(Y–Q)<Y and also, after comparing equation (4) with equation (2), we can state:

A₁ = B₁, where A₁<A; B₁<B (5)

Now we get a situation similar to the one with numbers A, B only with smaller numbers A₁, B₁. Analyzing now (5) in the manner described above we will be forced to admit that there must exist numbers

A₂=B₂, where A₂<A₁; B₂<B1 (6)

Following this path, we will inevitably come to the case when the existence of numbers A_k=B_k, where A_k<A_k-1; B_k<B_k-1 as a direct consequence of assumption (1) will become impossible. Therefore, our initial assumption (1) is also impossible and thus the theorem is proven.⁴¹

Looking at this very simple and even elementary proof by the descent method naturally a puzzling question arise, how could it happen that for many centuries science not only had not received this proof, but was completely ignorant that it had not any one in general? On the other hand, even being mistaken in this matter i.e. assuming that this theorem was proven by Euclid, how could science ignore it by using the "complex numbers" and thereby dooming itself to destruction from within? And finally, how can one explain that this very simple in essence theorem, on which the all science holds, is not taught at all in a secondary school?

As for the descent method, this proof is one of the simplest examples of its application, which is quite rare due to the wide universality of this method. More often, the application of the descent method requires a great strain of thought to bring a logical chain of reasoning under it. From this point of view, some other special examples of solving problems by this method can be instructive.

3.4. The Descent Method

3.4.1. A Little Bit of " Sharpness of Mind" for a Very Difficult Task

We will now consider another example of the problem from Fermat's letter-testament, which is formulated there as follows:

There is only one integer square, which increased by two, gives a cube, this square is 25.

When at the suggestion of Fermat, the best English mathematician of the time John Wallis tried to solve it, he was very vexed and forced to acknowledge he could not do it. For more than two centuries it was believed that Leonard Euler received the solution to this problem, but his proof is based on the use of "complex numbers", while we know these are not numbers at all because they do not obey the Basic theorem of arithmetic. And only at the end of the twentieth century André Weil using the Fermat's triangles method still managed to get a proof [17].

It was a big progress because a purely arithmetic method was used here, however, as applied to this problem, it was clearly dragged the ears. Could Fermat solve this problem easier? We will also extract the answer to this question from the cache, what will allow us to reveal this secret of science in the form of the following reconstruction. So, we have the equation p³=q²+2 with the obvious solution p=3, q=5. To prove Fermat's assertion, we suppose that there is another solution P>p=3, Q>q=5, which satisfies the equation

P³=Q²+2 (1)

Since it is obvious that Q>P then let Q=P+δ (2)

Substituting (2) in (1) we obtain: P²(P–1)–2δP–δ²=2 (3)

Here we need just a little bit of “sharpness of mind” to notice that δ>P otherwise equation (3) is impossible. Indeed, if we make a try δ=P then on the left (3) there will be P²(P–4)>2 what is not suitable, therefore there must exist a number δ₁=δ–P. Then substituting δ=P+δ₁ in (3) we obtain

P₂(P–4)–4δ₁P–δ₁²=2 (4)

Now we will certainly notice that δ₁>P otherwise, by the same logic as above, on the left (4) we get P²(P–9)>2 what again does not suitable, then there must exist a number δ₂=δ₁–P and after substituting δ₁=P+δ₂ in (4), we obtain P²(P–9)–6δ₂P–δ₂²=2 (5)

Here one can no longer doubt that this will continue without end. Indeed, by trying δ_i=P each time we get P²(P−K_i)>2. Whatever the number of K_i this equation is impossible because if K_i<P and P>3 then P²(P−K_i)>2 and if K_i≥P then this option is excluded because then P²(P−K_i)≤0

To continue so infinitely is clearly pointless, therefore our initial assumption of the existence of another solutions P>3, Q>5 is false and this Fermat's theorem is proven.

In the book of Singh, which we often mention, this task is given as an example of the “puzzles” that Fermat was “inventing”. But now it turns out that the universal descent method and a simple technique with trying, make this task one of the very effective examples for learning at school.

Along with this proof, students can easily prove yet another theorem from Fermat’s letter-testament, which could be solved only by such a world-famous scientist as Leonard Euler:

There are only two squares that increased by 4, give cubes, these squares will be 4 and 121.

In other words, the equation p³=q²+4 has only two integer solutions.

3.4.2. The Fermat’s Golden Theorem

We remind that in the Fermat's letter-testament only a special case of this theorem for squares is stated. But also, this simplified version of the task was beyond the power not only of representatives of the highest aristocracy Bachet and Descartes, but even the royal-imperial mathematician Euler.

However, another royal mathematician Lagrange, thanks to the identity found by Euler, still managed to cope with the squares and his proof of only one particular case of FGT is still replicated in almost all textbooks. However, there is no reasonable explanation that the general proof of the FGT for all polygonal numbers obtained by Cauchy in 1815 was simply ignored by the scientific community.

We begin our study with the formulation of the FGT from Fermat's letter to Mersenne in 1636. It is presented there as follows:

Every <natural> number is equal

one, two or three triangles,

one, 2, 3 or 4 squares,

one, 2, 3, 4 or 5 pentagons,

one, 2, 3, 4, 5 or 6 hexagons,

one, 2, 3, 4, 5, 6 or 7 heptagons,

and so on to infinity [36].

Since polygonal numbers are clearly not respected by today's science, we will give here all the necessary explanations. The formula for calculating any polygonal number is represented as

m_i = i+(k−2)(i−1)i/2

where m is a polygonal number, i is a serial number, k is the quantity of angles.

Thus, m₁=1; m₂=k; and for all other i the meaning of mi varies widely as shown in the following table:

Table 1. Polygonal numbers

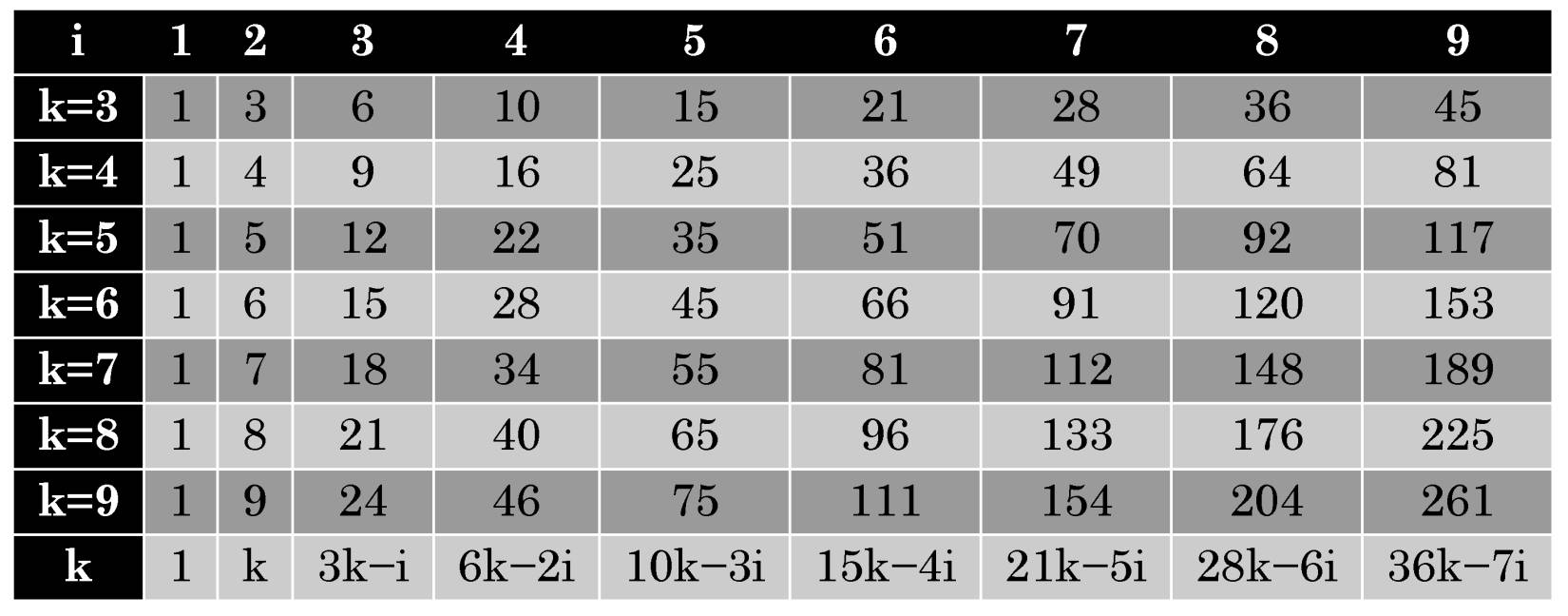
To calculate m_i it is enough to obtain only triangular numbers by the formula, which is very easily since the difference between them grows by unit with each step. And all other m_i can be calculated by adding the previous triangular number in the columns. For example, in column i=2, numbers increase by one, in column i=3 – by three, in column i=4 – by six etc. i.e. just on the value of the triangular number from the previous column.

To make sure that any natural number is represented by the sum of no more than k k-angle numbers is quite easily. For example, the triangular number 10 consists of one summand. Further 11=10+1, 12=6+6, 13=10+3 of two, 14=10+3+1 of three, 15 again of one summand. And so, it will happen regularly with all natural numbers. Surprisingly that the number of necessary summands is limited precisely by the number k. So, what is this miraculous power that invariably gives such a result?

As an example, we take a natural number 41. If as the summand triangular number will be closest to it 36, then it will not in any way to fit into three polygonal numbers since it consists minimum of 4 ones i.e. 41=36+3+1+1. However, if instead of 36 we take other triangular numbers for example, 41=28+10+3, or 41=21+10+10 then again in some unknown miraculous way everything will so as it stated in the FGT.

At first glance it seems simply unbelievable that it can somehow be explained? But we still pay attention to the existence of specific natural numbers, which are consisting at least of k k-angle numbers and denoted by us as S-numbers. Such numbers are easily to find for example, for triangles – 5, 8, 14, for squares – 7, 15, 23, for pentagons – 9, 16, 31 etc. And this our simple observation allows us directly to move to aim i.e. without using ingenious tricks or powerful "sharpness of mind".

Now to prove the FGT, suppose the opposite i.e. that there exists a certain minimal positive integer N consisting minimum of k + 1 k-angle numbers. Then it’s clear that this our supposed number should be between some k-angle numbers m_i and m_i+1 and can be represented as

N=m_i+δ₁ where δ₁=N−m_i (1)

It is quite obvious that δ₁ must be an S-number since otherwise this would contradict our assumption about the number N. Then we proceed the same way as in our example with the number 41 i.e. represent the supposed number as

N = m_i-1+δ₂ where δ₂=N−m_i-1

Now δ₂ should also be an S-number. And here so we will go down to the very end i.e. before

δ_i-1=N−m₂ =N−k and δ_i=N−m₁=N–1 (2)

Thus, in a sequence of numbers from δ₁ to δ_i, all of them must be S-numbers i.e. each of them will consist of a sum minimum of k k-angle numbers, while our supposed number N will consist minimum of k+1 k-angle numbers. From (1) and (2) it follows:

N− m_i =S_i (3)

Thus, if we subtract any smaller polygonal number m_i from our supposed number N then according to our assumption, the result should be only an S-number. Of course, this condition looks simply unbelievable and it seems that we are already at target, but then how can one prove that this is impossible? …

If we gave an answer to this question here, then this famous Fermat's theorem would immediately turn into the most common school problem and interest to it would be lost. To prevent this from happening, we will stay on the fact that the proof is presented here only by 99% and the remaining 1% will be offered to those who will be interested in order to appreciate the true magnificence of this scientific achievement of Fermat, especially in comparison with the Cauchy’s GFT proof.⁴²

Pic. 34. Title Page the Cauchy's Proof

of the Fermat's Golden Theorem

Pic. 35. One of 43 Pages the Cauchy's Proof

of the Fermat's Golden Theorem