Яков Перельман
Для юных математиков. Веселые задачи

Полная версия

РЕШЕНИЯ ЗАДАЧ №№ 1-10

Решение задачи № 1

Ниже указан самый короткий способ обмена. Цифры показывают, с какого пня на какой надо прыгать (напр., «1–5» значит: белка прыгает с пня 1-го на 5-й). Всех прыжков понадобится 16, а именно:

1-5; 3–7, 7–1; 8–4, 4–3, 3–7; 6–2, 2–8, 8–4, 4–3; 5–6, 6–2, 2–8; 1–5, 5–6; 7–1.

Решение задачи № 2

Для удобства мы заменим чайную посуду цифрами. Тогда задача представится в таком виде:

Надо обменять места 2 и 5. Вот порядок, в каком следует двигать предметы на свободный квадрат:

2, 5, 4, 2, 1, 3, 2, 4, 5, 1, 4, 2, 3, 4, 1, 5, 2.

Задача решается в 17 ходов – более короткого решения нет.

Решение задачи № 3

В этой таблице показаны в последовательном порядке все переезды, необходимые для того, чтобы вывести заведующего гаражом из затруднения. Цифры обозначают номера автомобилей, а буквы – соответствующие помещения. Всех переездов понадобится 43. Вот они:

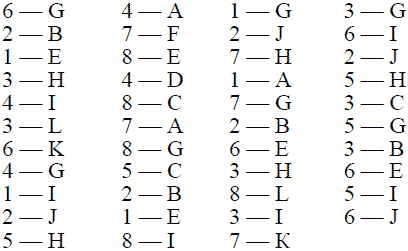
«6 – G» означает: автомобиль № 6 становится в отделение G, и т. п.

Решение задачи № 4

Три непересекающиеся пути показаны на этом чертеже:

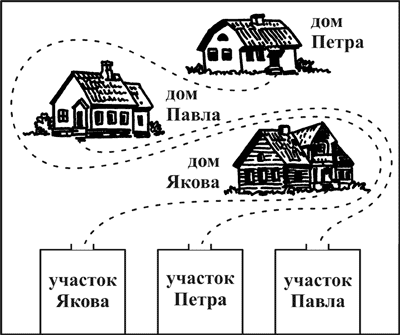
Рис. 11.

Петру и Павлу приходится идти довольно извилистыми путями, – но зато братья избегают нежелательных встреч между собой.

Решение задачи № 5

Стрелки на рисунке показывают, какие мухи переменили место и с каких клеток oни пересели.

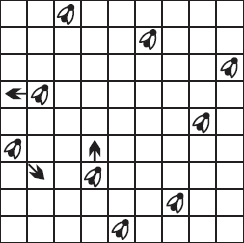
Рис. 12.

Решение задачи № 6

Забор можно построить двояко. Вот чертежи, показывающие направление ограды.

Забор, построенный по второму плану, короче и, следовательно, дешевле.

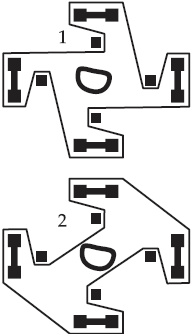
Рис. 13.

Решение задачи № 7

Вот единственное расположение, при котором два дома безопасны от нападения извне.

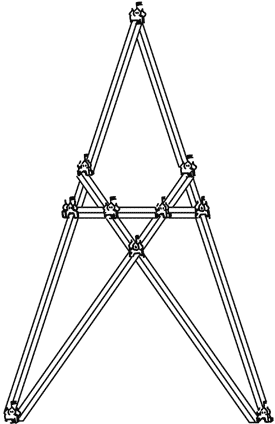
Рис. 14.

Вы видите, что 10 до мов расположены здесь, как требовалось в задаче: по 4 на каждой из пяти прямых стен.

Решение задачи № 8

Деревья, оставшиеся несрубленными, были расположены так (рис. 15):

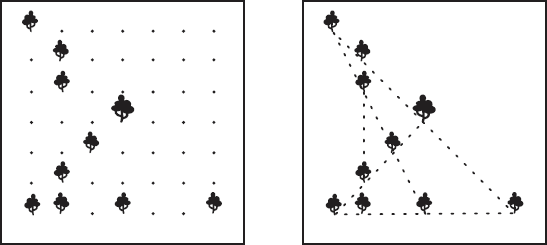
Рис. 15.

Как видите, они образуют 5 прямых рядов, и в каждом ряду 4 дерева.

Решение задачи № 9

Кошка должна съесть первой ту мышь, которая находится на нашем рисунке у копчика ее хвоста.

Попробуйте, начав с этой мыши счет по кругу, зачеркивать каждую 13-ю мышь, – вы убедитесь, что белая мышь будет зачеркнута последней.

Решение задачи № 10

Рис. 16.

На чертеже показано, как надо сложить из 18 спичек два четырехугольника, чтобы один был втрое больше другого по площади. Вторым четырехугольником является параллелограмм с высотою, равною 1 ¹/₂ спичкам.

Площадь параллелограмма равна его основанию, умноженному на его высоту. В основании нашего параллелограмма лежат 4 спички, высота же равна 1 ¹/₂спичкам; следовательно, площадь равна 4 x 1¹/₂, т. е. 6таким квадратикам, каких в меньшем четырехугольнике 2. Итак, нижний четырехугольник имеет площадь втрое большую, нежели верхний.

Глава II
Десять легких задач

ЗАДАЧА № 11

Бочки

В магазин доставили 6бочек керосину. На этом рисунке обозначено, сколько ведер было в каждой бочке. В первый же день нашлось два покупателя; один купил целиком две бочки, другой – три, причем первый купил вдвое менее керосина, чем второй. Не пришлось даже раскупоривать бочек.

Рис. 17.

И тогда на складе из 6 бочек осталась всего одна. Какая?

ЗАДАЧА № 12

До половины

В бочке налита вода, по-видимому, до половины. Но вы хотите узнать точно, половина ли в ней налита, или больше половины, или же меньше половины. У вас нет ни палки, ни вообще инструмента для обмера бочки. Втулки бочка не имеет. Каким образом могли бы вы убедиться, налита ли вода ровно до половины?

ЗАДАЧА № 13

Невозможное равенство

Кстати, о полупустой бочке. Полупустая бочка – это ведь то же, что и полуполная. Но если половины равны, то должны быть равны и целые. Полупустая бочка равна полуполной, – значит, пустая бочка должна равняться полной. Выходит, что пустой равен полному!

Почему получился такой несообразный вывод?

ЗАДАЧА № 14

Число волос

Как вы думаете: существует ли на свете два человека с одинаковым числом волос?

Вы ответите, пожалуй, что два совершенно лысых человека имеют волос поровну, потому что и у того и у другого ноль волос.

Это, если хотите, правильно.

Но я спрашиваю не о безволосых людях, а о таких, у которых имеются на голове густые волосы. Найдется ли в мире два человека, у которых число волос на голове было бы в точности одинаково?

А может быть, двое таких людей отыщутся в Ленинграде или Москве?

ЗАДАЧА № 15

Цена переплета

Книга в переплете стоит 2 руб. 50 коп. Книга на 2 рубля дороже переплета. Сколько стоит переплет?

ЗАДАЧА № 16

Цена книги

Иванов приобретает все нужные ему книги у знакомого ему книгопродавца со скидкою в 20 процентом. С 1-го января цены всех книг повышены на 20 процентов. Иванов решил, что он будет теперь платить за книги столько, сколько остальные покупатели платили до 1-го января. Прав ли он?

ЗАДАЧА № 17

Головы и ноги

На лугу паслись лошади под надзором кучеров. Если бы вы пожелали сосчитать, сколько всех ног на лугу, то насчитали бы 82 ноги. А если бы пересчитали головы, то оказалось бы, что всех голов – лошадиных и человеческих – 26.

Сколько было лошадей и сколько кучеров?

Надо заметить, что ни безногих лошадей, ни калек-кучеров на лугу не было.

ЗАДАЧА № 18

На счётах

Вы, без сомнения, умеете считать на конторских счётах и понимаете, что отложить на них 25 рублей – задача очень легкая.

Но задача станет замысловатее, если вам поставят условие: сделать это так, чтобы отодвинуть не 7 косточек, как обыкновенно, а 25 косточек.

Попробуйте, в самом деле, показать на конторских счётах сумму в 25 рублей, отложив ровно 25 косточек.

Конечно, на практике так никогда не делается, но задача все же разрешима, и ответ довольно любопытен.

ЗАДАЧА № 19

Редкая монета

Собирателю редкостей сообщили, что в Риме при раскопках найдена монета с надписью по-латыни:

55-й год до Р. X.

– Монета, конечно, поддельная, – ответил собиратель.

Как мог он знать это, не видя ни самой монеты, ни даже ее изображения?

ЗАДАЧА № 20

Спаржа

Женщина обыкновенно покупает у зеленщика спаржу большими пучками, каждый 40 сантиметров в окружности. Покупая, она мерит их, чтобы убедиться, что ее не обманывают. Но однажды у торговца не оказалось 40-сантиметрового пучка и он предложил покупательнице за те же деньги два тонких пучка, каждый по 20 сантиметров в обхвате.

Женщина обмерила два пучка и, убедившись, что обхват каждого действительно равен 20 сантиметрам, заплатила зеленщику столько же, сколько платила раньше за один толстый пучок.

Прогадала ли она или выгадала на этой покупке?

РЕШЕНИЯ ЗАДАЧ №№ 11-20

Решение задачи № 11

Первый покупатель купил 15-ведерную и 18-ведерную бочку. Второй – 16-ведерную, 19-ведерную и 31-ведерную. В самом деле:

15+18 = 33

16+19+31 = 66,

т. е. второй покупатель приобрел вдвое больше керосину, чем первый.

Осталась непроданной 20-ведерная бочка.

Это единственный возможный ответ. Другие сочетания не дают требуемого соотношения.

Решение задачи № 12

Рис. 18.

Самый простой способ – наклонить бочку так, чтобы вода дошла до края. Если при этом немного обнаружится дно бочки, – значит, вода стояла ниже половины. Если дно очутится ниже уровня воды, – значит, вода была налита больше, чем до половины. И наконец, если верхний край дна будет как раз на уровне воды, – значит, вода налита ровно до половины.

Решение задачи № 13

Полупустая бочка есть не половина пустой бочки, а такая бочка, одна половина которой пуста, другая – полна. Мы же рассуждали так, как будто слово «полупустая» значит: «половина пустой бочки», а «полуполная» – половина полной. Не удивительно, что при таком неправильном понимании мы пришли к неправильному выводу.

Решение задачи № 14

Прежде чем решить задачу, задайте себе вопрос:

Чего больше – людей на свете или волос на голове одного человека?

Разумеется, людей на свете неизмеримо больше, чем волос на голове. У нас волос на голове всего 150–200 тысяч, людей же на свете 1800 миллионов.

А если так, то необходимо должны существовать люди с одинаковым числом волос! И не только во всем мире, по даже в каждом многолюдном городе, насчитывающем больше 200 тысяч жителей. В Москве 1 ¹/₂ миллиона жителей, и, значит, десятки москвичей должны иметь число волос одинаковое. Ведь не может же быть 1 ¹/₂ миллиона различных целых чисел, из которых ни одно не больше 200.000.

Решение задачи № 15

Обыкновенно, не подумав, отвечают:

– Переплет стоит 50 копеек.

Но тогда ведь книга стоила бы 2 рубля, т. е. всего на 1 руб. 50 коп. дороже переплета!

Верный ответ: цена переплета – 25 коп., цена книги – 2 руб. 25 коп.

Решение задачи № 16

Иванов – как ни странно, – будет и теперь платить все же меньше, чем остальные покупатели платили до 1 января. Он будет получать 20 % скидки с цены, увеличенной на 20 %; другими словами, он будет получать скидку 20 % с 120 %, т. е. платить не 100 %, а всего лишь 96 % прежней цены книги. Трехрублевую книгу он приобретет не за 3 рубля, а за 2 руб. 88 коп.

Решение задачи № 17

Если бы все 26 голов на лугу были человеческие, мы насчитали бы не 82 ноги, а только 52, т. е. на 30 ног меньше. От замены одного человека лошадью число всех ног увеличилось бы на 2. Значит, чтобы насчитать 82 ноги, надо произвести подобную замену 15 раз – тогда и найдутся недостающие 30 ног.

Итак, из 26 голов 15 принадлежало лошадям, а остальные 11 – людям.

Решение задачи № 18

Двадцать пять рублей можно отложить на счётах 25-ю косточками следующим образом (рис. 19):

Рис. 19.

В самом деле: здесь отложено 20 руб.+4 руб.+90 коп.+10 коп. = 25 руб.

Число же косточек – 2+4+9+10 = 25.

Решение задачи № 19

Чеканя монету до Р X., римляне разве могли знать, что через 53 года родится Христос?

Решение задачи № 20

Покупательница прогадала. Пучок с двойным обхватом заключает в себе не вдвое, а вчетверо более спаржи, нежели тонкий пучок (рис. 20).

Рис. 20.

Женщина должна была либо заплатить вдвое меньше, либо же потребовать не два, а четыре тонких пучка.

Глава III
Десять задач потруднее

ЗАДАЧА № 21

Сколько прямоугольников?

Сколько прямоугольников можете вы насчитать в этой фигуре?

Не спешите с ответом. Обратите внимание на то, что спрашивается не о числе квадратов, а о числе прямоугольников вообще – больших и малых, – какие можно насчитать в этой фигуре.

Рис. 21.

ЗАДАЧА № 22

Реомюр и Цельсий

Вы знаете, конечно, разницу между термометрами Реомюра и Цельсия. Скажите же: всегда ли градусы на термометре Реомюра больше, чем градусы на термометре Цельсия?

Рис. 22.

ЗАДАЧА № 23

Столяр и плотники

Шесть плотников и столяр нанялись на работу. Каждый плотник заработал по 20 руб., столяр же – на 3 руб. больше, чем заработал, в среднем, каждый из семерых.

Сколько же заработал столяр?

ЗАДАЧА № 24

Девять цифр

Напишите по порядку девять цифр:

1 2 3 4 5 6 7 8 9.

Вы можете, не меняя их порядка, вставить между цифрами знаки плюс и минус таким образом, чтобы в сумме получилось ровно 100.

Нетрудно, например, вставив + и – шесть раз, получить 100 таким путем:

12+3–4+5+67+8+9 = 100.

Если хотите вставить + или – всего только 4 раза, вы тоже можете получить 100.

123+4–5+67–89 = 100.

Попробуйте, однако, получить 100, пользуясь знаками + и – всего только три раза!

Это гораздо труднее. И все же – вполне возможно, надо только терпеливо искать.

ЗАДАЧА № 25

Книжный червь

В моем книжном шкафу стоят на полке сочинения Пушкина в 8-ми томах, том к тому.

Приехав с дачи, я с досадой убедился, что летом книжный червь усердно сверлил моего Пушкина и успел прогрызть ход от первой страницы первого тома до последней страницы третьего тома.

Сколько всего страниц прогрыз червь, если в первом томе 700 страниц, во втором – 640, а в третьем – 670?

ЗАДАЧА № 26

Сложение и умножение

Вы, без сомнения, не раз уже обращали внимание на любопытную особенность равенств:

2+2 = 4

2x2 = 4.

Это единственный пример, когда сумма и произведение двух целых чисел (и при том равных) одинаковы. Вам, однако, быть может, неизвестно, что существуют дробные числа (правда, не равные), обладающие тем же свойством:

3+1 ¹/₂ = 4 ¹/₂

3x1 ¹/₂ = 4 ¹/₂,

Попытайтесь подыскать еще примеры таких же чисел. Чтобы вы не думали, что поиски напрасны, скажу вам, что таких чисел весьма-весьма много.

ЗАДАЧА № 27

Стрельба на пароходе

Хороший стрелок стоит у одного борта парохода, а у противоположного помещена мишень. Пароход движется так, как изображено длинной стрелкой на приложенном здесь чертеже.

Рис. 23.

Стрелок прицелился совершенно точно.

Попадет ли он и цель?

ЗАДАЧА № 28

Под водой

На обыкновенных весах лежат: на одной чашке – булыжник, весящий ровно 2 килограмма, на другой – железная гиря в 2 килограмма. Я осторожно опустил эти весы под воду. Остались ли чашки в равновесии?

ЗАДАЧА № 29

Как это сделано

Вы видите здесь деревянный куб, сделанный из двух кусков дерева: верхняя половина куба имеет выступы, входящие в выемки нижней части. Но обратите внимание на форму и расположение выступов и объясните: как ухитрился столяр соединить оба куска?

Рис. 24.

ЗАДАЧА № 30

Cкорость поезда

Вы сидите в вагоне железной дороги и желаете узнать, с какою скоростью он мчится. Можете ли вы это определить по стуку колес?