
Роман Юрьевич Акентьев
СПИН-финансы
Заплати себе первому
«Путь к богатству, если бы вам захотелось обрести его, так же прост, как, как путь к ближайшему рынку. Главными в деле обретения богатства являются два качества: трудолюбие и бережливость: это значит не тратить попусту ни времени, ни денег, а напротив, использовать их наилучшим образом». Бенджамин Франклин, «Автобиография».
Поэтому, как бы это дико не звучало, так важно сначала заплатить себе самому первому. А потом платить другим из того, что осталось.
Самый распространенный вопрос, а что делать, если денег и так не хватает, а тут надо себе первому платить? Кажется, что это не возможно. Возможно! Просто надо начать думать иначе (подробнее на этом остановимся в одной из следующих глав). В качестве рабочей гипотезы, предлагаю вам принять следующее утверждение:
Если человек живет на 100 %, то сможет жить и на 90 %, при этом существенно не изменяя свой образ жизни.
Просто поверьте, что это так. Потому что это действительно так.
Каждый раз, когда вам поступают деньги от работодателя, вам надо незамедлительно часть денег положить на свой сберегательный счет. Какой конкретно процент от заработанного дохода откладывать: 5 %, 10 %, 20 %, 30 %, 50 %? Зависит от вашей текущей финансовой ситуации, от уровня ваших доходов и расходов, ваших финансовых целей и сроков их достижения, а также от того, насколько сильно вы готовы «затянуть пояса», ради достижения своих финансовых целей (об этом подробнее поговорим в главе про планирование).
«Никто не становится богатым лишь в силу того, что много зарабатывает. Богатство возникает, если вы сохраняете деньги. Поэтому начинайте экономить сейчас. Совершенно неважно, в какой сложной ситуации вы находитесь. Легче, чем сегодня, не будет никогда. Начните сейчас с того, чтобы экономить 10 процентов Вашего чистого дохода». Бодо Шафер, «Путь к финансовой независимости»
У сбережения есть два момента, на которые стоит особо обратить внимание:
1) Чем больший процент своего дохода сможете сберегать, и 2) Чем раньше начнете сберегать часть своего заработка, тем раньше сможете создать источники пассивного дохода, которые позволят вам не только реализовать ваши финансовые цели, но также «выйти на пенсию» раньше, чем это предписывается государством.
Умозрительно эти моменты (а по сути, речь идет о сложном проценте) достаточно тяжело осознать, поэтому рассмотрим их на примере банковского вклада. Для наглядности будем рассматривать без учета инфляции (подробнее влияние инфляции обсудим далее).
Допустим, есть два друга – Иван и Петя, – которые вместе отучились в ВУЗе, получили одинаковую профессию, трудоустроили на одну и ту же должность, и получают одинаковую зарплату – пусть будет 30 тыс. руб. в месяц. В целом, у них все одинаковое, за исключением подхода к управлению личными финансами.
В 25 лет, один из друзей (Иван), решил откладывать 10 % своего ежемесячного заработка на банковский вклад, под 10 % годовых. Каждый месяц, на протяжении 10 лет, он относил 10 % своего дохода в банк. За первый год он сберег 36 тыс. руб., за второй еще 36 тыс. руб. (в сумме уже 72 тыс. руб.) и т.д. За 10 лет он сберег суммарно 360 тыс. руб. Так как у него деньги лежали на банковском вкладе под 10 % годовых, то его сбережения увеличивались каждый год. В итоге, за 10 лет в сумме у него на счету оказалось уже более 600 тыс. руб. Откладывая по 10 % своего дохода ежемесячно, то есть по 3 тыс. руб., в 35 лет он стал обладателем 600 тыс. руб.
После этого Иван решил, что не будет больше делать взносов на банковский вклад. При этом его сбережения продолжали находиться на банковском депозите под 10 % годовых. Итак, деньги находятся в банке, но он больше не делает ежемесячный взнос в размере 3 тыс. руб.
При этом второй друг (Петя), с 25 до 35 годов тратил весь свой заработок и ничего не сберегал. Однажды он заметил, что его друг Иван, как-то незаметно, за прошедшие 10 лет, при том же самом уровне дохода сумел создать достаточно внушительные сбережения. У него нет ничего, а у друга целых 600 тыс. руб. есть на счету! И Петя решает также начать откладывать по 10 % своего ежемесячного дохода, то есть по 3 тыс. руб. Допустим, он продолжает сберегать ежемесячно по 3 тыс. руб. все следующие 30 лет, вплоть до выхода на пенсию в 65 лет. За эти 30 лет он сбережет в сумме 1 080 тыс. руб. (то есть в 3 раза больше, чем его друг). С учетом процентов по вкладу, размер его сбережений составит почти 6,8 млн. руб.
При этом Иван, за следующие 30 лет, то есть с 35 до 65 лет, не сделал ни одного дополнительного взноса на свой вклад (который он создавал с 25 до 35 лет). Напомним, что его вклад просто 30 лет лежал в банке под 10 % годовых.
В это трудно поверить, но суммарный размер его вклада оказался больше!
Не смотря на то, что Иван создавал свой актив 10 лет и внес 360 тыс. руб., а затем 30 лет ничего не делал, а при этом Петя первые 10 лет ничего не делал, но следующие 30 лет делал взносы (суммарно в 3 раза больше, чем первый), в итоге к 65 годам у Ивана вклад оказался существенно больше, чем у Пети – около 10,7 млн. руб., против 6,8 млн. руб.!
При этом у Ивана процентный доход равен 89 тыс. руб. в месяц, а у Пети лишь 56 тыс. руб. в месяц! Почувствуйте разницу!
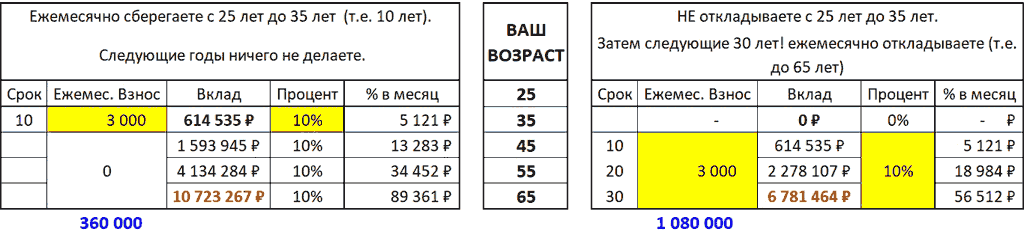
Таблица 1. Пример роста вклада каждого из двух друзей (в данном примере речь идет только о номинальных величинах, т. е. без учета инфляции).
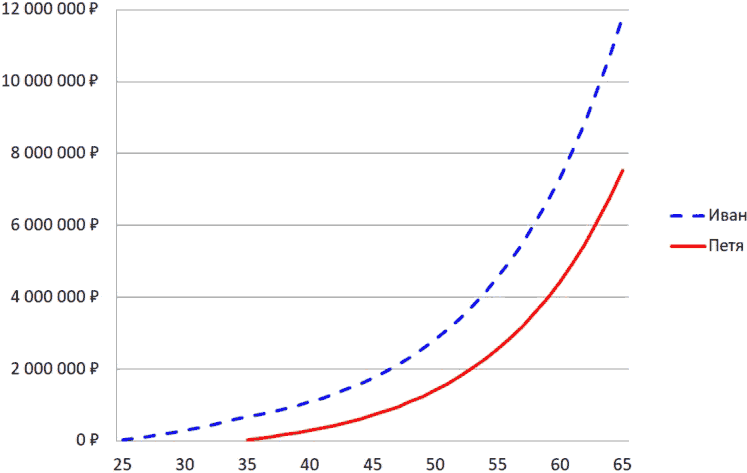
Рисунок 11. График роста вклада каждого из двух друзей.
На этом простом примере двух друзей видно, чем больше времени для инвестирования, тем в большей степени сказывается влияние эффекта сложного процента. Поэтому время, это одно из самых больших преимуществ для инвестора. Чем раньше человек начинает инвестировать, тем большему эффекту сложного процента подвергнутся его сбережения. Рассмотрим это на следующем примере. Допустим, был еще третий друг Сергей, который с 25 до 65 лет включительно ежемесячно сберегал по 3 000 руб. под 10 % годовых.
Еще раз обращаем ваше внимание на тот факт, что:
• Иван делал взносы 10 лет (с 25 лет до 35 лет), общая сумма взносов 360 тыс.;
• Петя делал взносы 30 лет (с 35 лет до 65 лет), и внес суммарно более 1 млн. руб.;
• Сергей делал взносы 40 лет (с 25 до 65 лет), суммарно внес 1,44 млн. руб.
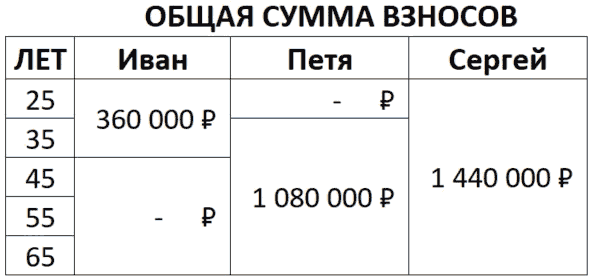
Таблица 2. Общая сумма взносов каждого из трех друзей на протяжении 40 лет.
Ниже показан график роста вклада каждого из трех друзей на протяжении 40 лет:
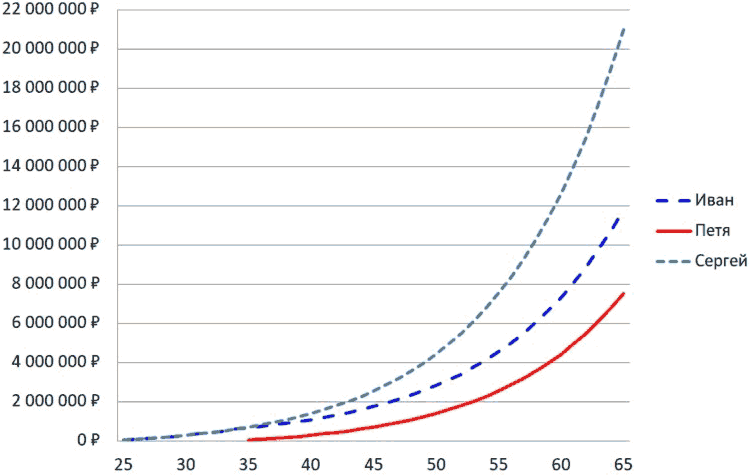
Рисунок 12. График роста вклада каждого из трех друзей.
ВАЖНО! Начинайте сберегать и инвестировать как можно раньше!
Резюмируем. Нельзя начать сберегать слишком рано, но может оказать слишком поздно.
При прочих равных:
• чем в более молодом возрасте (лет) вы начнете сберегать и инвестировать, тем больше будет ваш капитал, и тем больше у вас будет шансов на успешное достижение (реализацию) ваших финансовых целей;
• чем больше периодический взнос (рубли), тем больше будет ваш капитал;
• чем больший процент доходности (процент) могут обеспечить ваши инвестиции, тем больше будет ваш капитал.
Игры с цифрами или 1 миллион долларов
Прежде чем, мы продолжим дальше, предлагаем немного «поиграть» с цифрами.
Итак, как мы только что видели, есть три взаимосвязанных параметра, которые оказывают влияние на размер будущего капитала:
• Время (горизонт планирования, то есть сколько лет вы собираетесь создавать требуемый капитал);
• Взнос (величина периодического платежа, то есть какую сумму в месяц или в год собираетесь инвестировать);
• Процент (определяет требуемую доходность инвестиции).
Взаимосвязь между параметрами довольно проста: увеличивая один из параметров, другой параметр можно уменьшать, при условии неизменности третьего параметра.
Например, через год (то есть параметр время не изменяется) требуется накопить определенную сумму на банковском депозите. Так вот, чем больше процентная ставка, тем меньше ежемесячный взнос можно делать. Или, чем больше ежемесячный взнос под тот же самый процент (то есть теперь неизменный параметр это процентная ставка), тем меньше времени потребуется для накоплений этой суммы.
Представьте ситуацию: вы открыли вклад в банке, в размере 1 доллар США, под 5 % годовых. Как вы думаете, сколько лет потребуется 1 доллару увеличиться до 1 миллиона долларов? Чуть менее 300 лет! А если быть точнее, то сумма в размере 1 041 743 долларов будет на счету через 284 года.
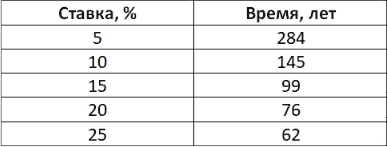
Таблица 3. Сколько лет потребуется 1 доллару увеличиться до 1 млн. долларов в зависимости от процентной ставки.
Данная таблица наглядно демонстрирует, как при одной и той же сумме требуемого капитала (1 миллион), изменяется горизонт планирования (срок вклада) в зависимости от процентной ставки. Чем больше процентная ставка, тем меньше лет требуется для достижения данной суммы.
Понятно, что ждать сотни лет это достаточно долго. Как мы можем повлиять на ситуацию? Вспоминаем про взаимосвязь между параметрами (время, взнос, процент): один параметр неизменный, другой параметр увеличиваем, тем самым можно уменьшить третий. Если нам не хочется ждать столько лет, пока появиться 1 миллион долларов, что можно сделать следующее:
• Если нам надо уменьшить параметр время, следовательно,
• Надо увеличить параметр взнос, при условии,
• Неизменности процентных ставок.
Давайте посмотрим, как изменится ситуация, если мы будем откладывать по одному доллару каждый день (то есть увеличиваем параметр взнос) на вклад с ежедневной капитализацией процентов.
Кстати, даже если вклад будет открыт на условиях ежемесячной капитализации, то количество лет не изменится. Просто в этом случае суммарная величина вклада будет чуть меньше (что в данном примере не имеет большого значения).
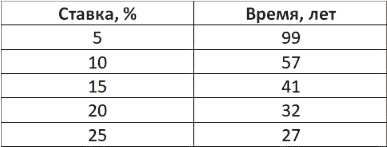
Таблица 4. Откладывая по 1 доллару ежедневно, сколько лет потребуется лет, чтобы вклад увеличился до 1 млн. долларов в зависимости от процентной ставки.
Как видим, ситуация изменилась кардинальным образом. Теперь уже вполне реально на протяжении трудовой деятельности (то есть порядка 40–50 лет) стать миллионером делая ежедневные взносы в размере всего лишь 1 доллар. Если начать в 20 лет откладывать по 1 доллару каждый день под 15 % годовых, то к выходу на пенсию, то есть в 60 лет, на счету будет заветный 1 миллион долларов!
По 1 доллару каждый день, следовательно, 365 долларов в год. За 40 лет в сумме величина взносов составит 14 610 (+ 10 долларов за каждый високосный год).
Итак, за в течении 10 лет вы внесете своих денег лишь 14 610 долларов, а на счету будет 1 миллион!
В этом и заключается сила сложного процента!
В таблице ниже показано количество лет (на пересечении соответствующего столбца и ряда), которое потребуется для создания 1 млн. долларов при заданном ежедневном взносе и заданной годовой процентной ставкой (ежемесячная капитализация процентов).
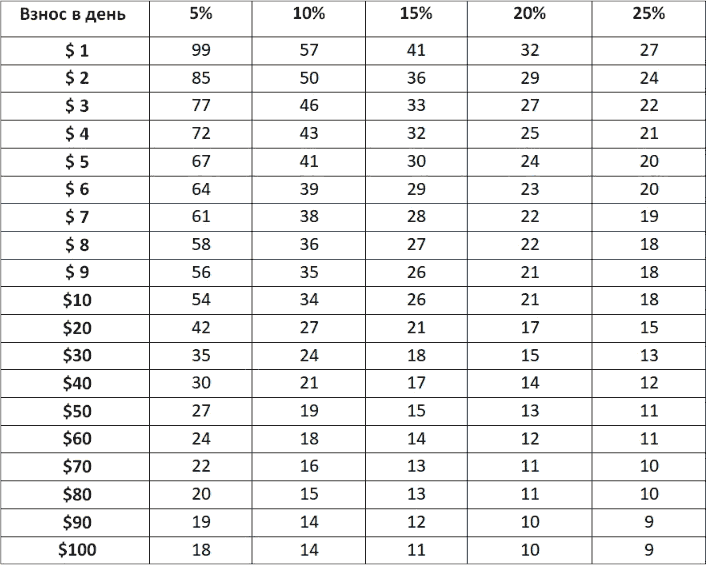
Таблица 5. Количество лет, которые потребуются для создания 1 млн. долларов, при заданной процентной ставке и заданной величине ежедневного взноса.
Очевидно, что рост сложного процента не очевиден. Сложные проценты увеличиваются не интуитивным образом. Просто с трудом верится, что буквально несколько долларов в день могут в обозримом будущем стать миллионом. Пусть и номинальным (покупательная способность будет не та – инфляция), но все-таки миллионом!
Сколько сейчас стоит доллар в рублях? А сколько рублей в день у вас уходит не понятно на что, не понятно куда? А ведь эти «мелкие расходы» (да плюс целенаправленно сберегаемые рубли) могли бы оказаться на банковском или брокерском счету, где бы работали на вас годами…
Основы финансовых вычислений
Процент
Теперь попробуем разобраться, как устроены проценты и в чем их сила?
Чтобы понять силу сложных процентов, сначала надо разобраться, что такое процент сам по себе. Слово «процент» происходит от латинского «per cent», что означает «на сотню». То есть процент есть не что иное, как одна сотая часть и его стандартным обозначением при записи является знак «%».
Достаточно наглядно это можно увидеть на примере в Excel. Если вы создадите новую книгу, и в любой ячейки поставите, например, цифру 5, а затем поменяете числовой формат ячейки на процентный, то значение в ячейки станет равным 500 %, то есть в сто раз больше. Соответственно, если введете цифру 5 в ячейку с процентным форматом, то есть у вас будет 5 %, а затем поменяете формат ячейки на числовой, то значение поменяется на 0,05, то есть в сто раз меньше станет.
Таким образом, если после числа стоит значок «%», то для привидения его к числовому формату данной число следует просто разделить на сто и убрать обозначение процента, то есть знак «%» (15 % и 0,15 это эквивалентные записи одного и того же). Для того чтобы число преобразовать в процентный формат, его следует наоборот умножить на 100 и поставить знак процента (1,25 = 125 %).
Например, 15 % от 600 кг означает 15 частей по 6 кг каждая (потому что, одна сотая от 600 кг есть 6 кг). Таким образом, чтобы найти чему равно 15 % от 600 кг, надо 15 умножить на 6 кг (или 15 раз сложить по 6 кг), что в сумме даст 90 кг. Верно также и то, что 200 % от 500 руб. есть 1 тыс. руб., так как 1 % равен 5 рублям, а 5 руб. × 200 = 1 тыс. руб.
Кстати, следует не путать термины «вырос на Х%» и «вырос в Х раз». Если ваша инвестиция выросла в 2 раза, то это означает 100 % рост. А если у вас было на брокерском счету 1 000 тыс. руб., а теперь 700 тыс. руб. это означает изменение на «-30 %», что эквивалентно изменение в 0,7 раз.
То есть изменение в Х раз это то же самое, что изменение на (Х-1)*100 % (где Х любое число).
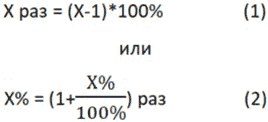
При этом, если Х>1, то это будет рост (ваших активов, вкладов, цен, стоимости, курсов и т.д.), а если Х<1, то это будет падение/уменьшение.
• Например, цены выросли в 2,5 раза. На сколько процентов изменились цены? Считаем по формуле 1:
(2,5–1)*100 % = 1,5*100 % = 150 %.
Ответ: цены выросли на 150 %.
• Например, цены упали на 15 %. Во сколько раз изменились цены?
Считаем по формуле 2:
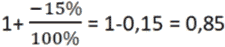
Ответ: цены изменились в 0,85 раз, то есть произошло падение цен.
Процентная ставка
С позиции денежной теории, у денег, как у средства сбережения (накопления), есть своя цена. Этой ценой является процентная ставка.В жизни, люди иногда занимают у знакомых незначительные суммы на непродолжительный срок (например, 1 тыс. руб. на неделю). Как только появляются деньги, люди возвращают долг плюс, возможно, дарят шоколадку рублей за 50, в качестве ответного знака благодарности за то, что человек (в данном случае выступающий в роли кредитора) выручил и дал взаймы. Кстати, в этом примере, если подарить шоколадку, то она тогда будет выступать в роли «процентов» за пользование кредитом. Если же ничего не дарить в ответ, тогда можно считать, что у человека просто был беспроцентный краткосрочный займ.
Процентная ставка – это сумма, указанная в процентном выражении к сумме кредита, которую платит получатель кредита за пользование кредитом в расчете на определенный период (месяц, квартал, год).
На заметку. Если в данном примере, вы попробуете самостоятельно подсчитать «годовую процентную ставку», исходя из стоимости шоколадки (50 руб.), рассматривая ее как плату за пользования кредитом (1 000 руб. на 7 дней), то получатся умопомрачительные проценты. НО!
Важно обратить внимание на то, что помогать друзьям, товарищам, родным и близким за 50 рублей и помогать бесплатно – это не одно и то же. Каждый из нас одновременно живет в двух мирах: в мире социальных отношений и в мире экономических отношений. И собственное поведение, и поведение других людей каждый оценивает либо с точки зрения рыночных норм, либо социальных. И очень важно не перепутать эти два мира. Когда один мир проникает в другой – могут разрушиться оба.
Одно дело приятно провести вечер со своей второй половинкой и лечь в кровать вместе тесно прижавшись к друг другу. А утром приготовить завтрак, нежно чмокнуть засоню в щеку и убежать на работу. Другое дело вместо завтрака оставить пару тысяч и записку: «Вечер был великолепен. Ты просто супер!». Согласитесь, ведь подобное отношение просто раздавит близкого человека, не так ли?
В социальном мире «платежи» являются не явными – это может быть нежные поглаживания, обнимания, ласковые слова, похвала и признание усилий и вклада партнера в общее дело и т.д.
В экономическом мире «платежи» являются явными и измеряются в рублях или в чем-то материальном.
Главное не перепутать одно с другим.
В случае необходимости крупных сумм на длительные сроки, не всегда есть возможность взять в долг у знакомых. Чем больше требуется сумма в долг (и чем больше срок), тем меньше шансов, что найдется желающий их предоставить. Это не совсем очевидно, но на это есть несколько причин. Давайте попробуем разобраться.
Временная ценность денег
Одним из важнейших свойств денежных потоков (потоков наличных денег, учитывающих все поступления денежных средств и платежи) является их распределенность во времени. В условиях стабильной экономики на краткосрочных периодах это свойство не имеет большого значения и им можно пренебречь. Но в случае длительных периодов и/или сильной инфляции возникает проблема сопоставления данных. Одно и то же номинальное количество денег, полученное с интервалом в 1 год, будет иметь неодинаковую ценность. Например, вспомните последний валютный кризис – 1 тыс. руб. в декабре 2013 году и 1 тыс. руб. в декабре 2014 года, это уже разные вещи.
Но проблема не сводится только к учету инфляции. Одно из самых важных понятий в мире финансов является временная ценность денег.[3] Временная ценность денег показывает зависимость реальной стоимости от величины промежутка времени, остающегося до их получения или расходования. В экономической теории данное свойство называется временным предпочтением.
В экономической теории различают положительное, нулевое и отрицательное временное предпочтение.
• Положительное временное предпочтение означает, что более 1 ден. ед. в будущем требуется для компенсации отказа от возможности тратить 1 ден. ед. в текущем периоде;
• Нулевое временное предпочтение означает, что потребитель откажется от 1 ден. ед. текущего дохода в обмен на 1 ден. ед. дохода через год, так что его благосостояние останется прежним. Потребитель с нулевым временным предпочтением не потребует никакого процента на свои сбережения;
• Отрицательное временное предпочтение означает, что потребитель будет делать сбережения, даже если откладывание 1 ден. ед. текущего дохода обернется возвратом менее 1 ден. ед.
Наряду с инфляционным обесцениванием денег существует еще несколько причин положительного временного предпочтения. Одна из причин заключается в том, что «сегодняшние» деньги будут всегда ценнее «завтрашних» из-за риска неполучения последних. Этот риск тем больше, чем больше промежуток времени, отделяющий получателя денег (кредитора) от этого завтра. Другая причина состоит в том, что располагая денежными средствами «сегодня», человек (домохозяйство, предприятие и т.д.) может вложить их в какое-либо дело и заработать прибыль, тогда как получатель будущих денег лишен такой возможности. Таким образом, владелец денег не только подвергает себя риску не возврата денег, но и несет реальные экономические потери в форме не полученных доходов от инвестирования. При этом любые обязательства по возврату денежных средств, получаемые взамен денег, имеют существенно низкую ликвидность, чем наличные деньги. Риск потери ликвидности еще одна причина положительного временного предпочтения.
Наращивание и дисконтирование
Учитывая все вышеперечисленные факторы, владельцы денег, обычно, не согласны бесплатно принимать на себя все эти риски. Поэтому, расставаясь с «сегодняшними» деньгами (выдача кредита), владельцы денежных средств устанавливают такие условия возврата денег, которые должны полностью возместить все сопутствующие риски. Количественной мерой величины этого возмещения как раз и является процентная ставка.
С помощью процентной ставки можно определить как будущую стоимость «сегодняшних» денег (в случае если их собираются отдать в долг), так и приведенную (современная, текущая, настоящая) стоимость завтрашних денег (то есть когда обещают расплатиться за поставленный товар или оказанную услугу через несколько месяцев). В первом случае говорят об операции наращивания, поэтому часто будущую стоимость денег называют наращенной. Во втором случае выполняется дисконтирование или приведение будущей стоимости к ее современной величине (текущему моменту) – отсюда термин дисконтированная, приведенная или текущая стоимость. Дисконтирование это наращивание «наоборот». Процентная ставка является показателем интенсивности изменения стоимости денег во времени, а абсолютная величина этого изменения и есть процент, который измеряется в денежных единицах (в нашем случае в рублях).
По сути, временная ценность денег гласит, что деньги должны приносить прибыль; таким образом, некоторая сумма сейчас стоит больше, чем эта же сумма потом, так как вложенная сейчас сумма принесет прибыль потом.
Проявление эффекта положительного временного предпочтения легко увидеть на психологическом уровне. Если вам предложить на выбор:
1) 1 млн. руб. сейчас, или
2) 1 млн. руб. через 3 года.
Что вы выберите? Скорее всего, вы выберете первый вариант (как и большинство), так как ждать целых три года не хочется.
Например, Коля выбрал первый вариант, а Толя второй. Коля оказался с деловой хваткой и вложил в их в прибыльное дело, которое принесло ему 20 % годовых в среднем (про вычисление средней доходности поговорим подробнее далее в этой главе). Итак, 1 млн. руб. это исходная сумма, а 728 тыс. руб. это суммарные проценты за три года нарастающим итогом.
Итого, 1 728 тыс. руб. – это наращенная сумма или будущая стоимость 1 млн. руб. через 3 года при условии 20 % ежегодной доходности.
А Толя хранил все это время деньги дома, в стеклянной банке на балконе… Наращенная сумма в случае Толи, в конце того же периода, составила 1 млн. руб. Теперь зададимся вопросом, если это наращенная сумма, то какова была исходная сумма, которую получил бы Толя сейчас? Производя операцию дисконтирования, получаем, что исходная сумма для Толи, в данном случае, равнялось бы примерно 578,7 тыс. руб.
И не так сложно ответить на достаточно простой вопрос: что лучше – иметь в настоящее время 578 тыс. руб. или 1 млн. руб.?




