
Петр Путенихин
О сущности ускоренного расширения Вселенной
О сущности ускоренного расширения Вселенной
В наших рассуждениях мы постоянно использовали понятие ускоренного, равномерного или замедленного расширения Вселенной. Однако чёткого определения этих понятий, что мы под ними подразумеваем, мы пока не привели. Более того, представления о механизмах, лежащих в их основе, весьма неопределённые и у многих других исследователей. Вследствие этого возникают довольно спорные выводы по проявлениям этих механизмов. В частности, существует мнение, что ускоренное расширение Вселенной напрямую связано с уменьшением параметра Хаббла во времени. Если параметр Хаббла уменьшается, то это означает ускоренное расширение Вселенной. Сторонники этого подхода приводят, например, аргумент, уравнение, который, по их мнению, определённо подтверждает такое мнение:
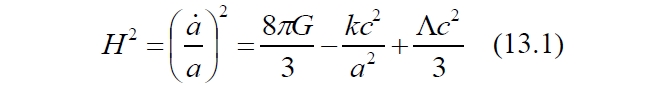
Утверждается, что вид этой формулы лишает всякой возможности придумать убывающую функцию масштабного фактора a(t), при которой убывал бы и параметр Хаббла. Действительно, из этого уравнения, на первый взгляд, явно следует, что росту масштабного фактора соответствует убывание параметра Хаббла. Однако перепишем уравнение условно и кратко:
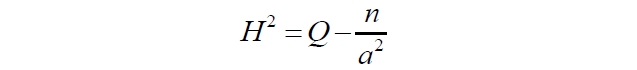
Теперь уже точно видно: при росте масштабного фактора a параметр Хаббла H может только возрастать! Это происходит из-за знака минус перед членом, содержащим масштабный фактор, в результате чего при его росте вычитается всё меньшая и меньшая величина, а результат, соответственно, возрастает.
Заметим, что и само понятие "ускоренное расширение Вселенной" имеет некоторую двусмысленность. Все объекты в расширяющейся Вселенной по определению движутся с ускорением. В самом деле, масштабный фактор Вселенной, пространство которой расширяется равномерно, описывается уравнением:
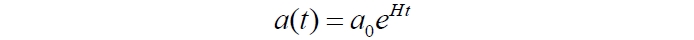
Это уравнение и собственно масштабный фактор и его производная по времени относятся ко всей Вселенной в целом, описывает каждую точку его пространства. В наблюдательной астрономии у них есть физические эквиваленты: конкретные дистанции между объектами (например, в световых годах) и скорости убегания (например, в долях от скорости света). Эти эквиваленты, соответственно, относятся только к этим двум объектам. В дальнейшем мы не будем акцентировать внимание на отмеченных особенностях, а просто будем подразумевать их тождество. В приведённой записи имеется в виду некоторый нулевой момент времени, когда масштабный фактор был ненулевым, равным некоторому начальному значению a0. Соответственно, эти два эквивалентных подхода имеют и эквивалентные уравнения:
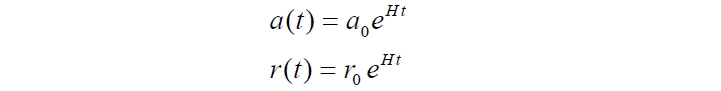
Обе величины – масштабный фактор и дистанция можно связать единичным коэффициентом:
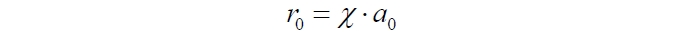
Смысл коэффициента – это длина, например, стандартного метра r0 в пространстве с масштабным фактором a0. Дифференцированием находим и такую же связь между скоростями изменения этих величин, представляющую закон Хаббла:
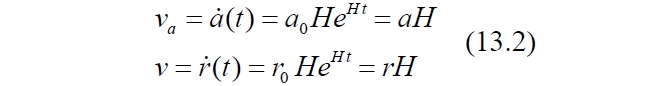
C учётом коэффициента находим выражение, которое выглядит, по сути, как простая замена переменных:
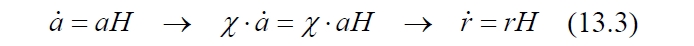
Хотя обычно мы оперируем масштабными факторами, это же уравнение, как видим, можно записывать и с реальными физическими переменными – скоростью и удалённостью.
Существует общепризнанная гипотеза, что обнаруженное ускоренное расширение Вселенной вызвано действием тёмной энергии. Но все объекты удаляются друг от друга с ускорением и в равномерно расширяющейся Вселенной. Из (13.3) мы явно видим, что скорость убегания объекта непрерывно возрастает. Это видно и из уравнений (13.2). Двойное дифференцирование показывает, что объекты не только удаляются с некоторым ускорением, но и само ускорение непрерывно растёт:
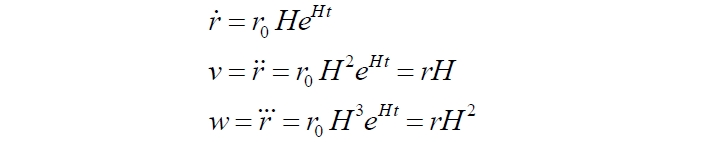
Уравнение для ускорения весьма похоже на стандартный закон Хаббла. Сразу же замечаем некоторые странности в трактовке таких ускорений. Понятно, что любой удаляющийся во Вселенной объект обладает некоторой массой. Следовательно, для его ускоренного движения необходимо приложить к нему какую-то силу, затратить некоторую энергию:







