Герман Иванович Ефремов
Макрокинетика сушки

Полная версия

Предисловие

Предлагаемая читателю монография “Макрокинетика сушки” относится к циклу инженерных дисциплин. Необходимость появления данной книги обусловлена тем, что вопросы макрокинетики процессов сушки и, в общем случае нестационарных процессов в химической, пищевой и текстильной технологии, недостаточно широко освещены в современной литературе. В то же время переход от линейных задач к нелинейным является характерным для описания множества современных технологических процессов, что и определяет актуальность появления данной книги.

Макрокинетика процессов переноса массы, тепла и импульса, что характерно и для процессов сушки, как самостоятельный раздел науки впервые была выделена профессором Д. А. Франком-Каменецким. Им, по словам академика Н. Н. Семенова, показано, что вопросы, рассматриваемые в этом разделе науки, имеют не только частное и прикладное, но и общенаучное значение и представляют общий теоретический научный интерес.

Общеизвестна фундаментальная монография Д. А. Франка-Каменецкого “Диффузия и теплопередача в химической кинетике”, выдержала три издания на русском языке и переиздана за рубежом. В ней автор рассматривает макрокинетику химических реакций и теорию горения в сочетании с диффузией, теплопередачей и гидродинамикой. Такое сочетание позволило решить ряд прикладных нелинейных задач, разработать новые методы расчета кинетики химических реакций и ряда нестационарных технологических процессов.

В развитие исследований макрокинетики процессов переноса внесли свой вклад такие известные ученые как академик Н. М. Жаворонков (теория гидродинамики и процессов химической технологии), профессор О. Левеншпиль (расчет и инженерное оформление химических реакторов), академик В.В. Кафаров (математическое моделирование химико-технологических процессов), профессор Я. Циборовский (тепло массообменные процессы) и многие другие исследователи.

Вопросы макрокинетики процессов рассматриваются также в настоящее время и под другими названиями “Теория диссипативных структур” – изучение диссипативных процессов, “Синергетика”– наука, изучающая периодические химические реакции и пространственную их картину, “Теория катастроф” – описание быстропротекающих процессов от механики полимеров до биологических процессов. “Теория катастроф” берет свое начало от теории теплового взрыва, разработанной академиком Н. Н. Семеновым, профессорами Д. А. Франком-Каменецким и О.М. Тодесом.

Макрокинетика процессов переноса массы, тепла и импульса получила свое дальнейшее развитие, особенно в конце двадцатого и начале этого века. Назрела необходимость в обобщении накопленного материала применительно к процессам сушки. Настоящая книга и представляет собой попытку рассмотрения сушки на основе новых теоретических принципов, а также ее описание на основе современных экспериментов по кинетике сушки и ряда других нестационарных процессов обработки различных материалов.

Известно, что явления переноса обусловлены как тепловым движением микрочастиц (молекулярная диффузия, теплопроводность) и такой перенос определяет микрокинетику процессов, так и, что наиболее часто, наличием конвективных токов и такой перенос определяет макрокинетику процессов. Влияние конвективных токов значительно превосходит по интенсивности молекулярный перенос. Именно поэтому, в названии монографии использован термин макрокинетика, как наиболее важный и определяющий тип переноса для большинства процессов.

В книге приведены экспериментальные данные, которые были получены на кафедрах процессов и аппаратов Московского государственного открытого университета им. В. С. Черномырдина и Московского государственного текстильного университета им. А.Н. Косыгина, а также и литературные данные по сушке различных материалов.

Автор выражает большую благодарность доктору техн. наук, проф. А.П. Булекову, рецензенту монографии, за его ценные замечания и советы, сделанные при рецензировании рукописи книги, а также Д.М. Курм за корректуру книги.

Основные обозначения

Латинские

Греческие

Индексы

Введение

Широкое использование разнообразных сорбционных материалов (волокнистых, пленочных, дисперсных) в различных отраслях промышленности, медицине и в космической технике диктует необходимость теоретического и экспериментального исследования их, как объекта обработки, исследования их сорбционных свойств, гидродинамики процессов обработки и кинетики протекающего при этом тепло- массообмена, как правило, нестационарного. Примерами широкого использования сорбционных процессов являются в первую очередь пищевая, химическая и текстильная промышленность.

На всех стадиях получения сорбционных материалов, их переработки и эксплуатации, протекающие диффузионные процессы тесно связанны с сорбционными свойствами этих веществ. Так, например, протекание и время окончания таких диффузионных процессов как увлажнение и сушка определяется изотермами сорбции-десорбции обрабатываемых материалов, отражающими сорбционные свойства веществ, которые в свою очередь определяются их структурой.

В то же время пористая структура материалов во многих случаях может быть определена на основании анализа изотерм сорбции-десорбции обрабатываемых материалов. Следует отметить, что определение пористой структуры материалов является достаточно сложной технической задачей и для этого часто необходимо уникальное оборудование.

Изменение структуры, сорбционных свойств и кинетики диффузии при обработке пищевых материалов во многом определяет их качество. Для материалов, применяемых в текстильной промышленности сорбционные процессы также важны, так как они подвергаются многократной влажностно-термической отделочной обработке. Отделочное производство в текстильной промышленности является очень энергоемким, здесь расходуется до 80 % всей тепловой энергии, расходуемой в производстве волокон и тканей. В этом производстве энергоемкими являются процессы сушки и промывки, поэтому их рассмотрение, наряду с крашением, представляет большой интерес.

Вместе с тем, надо отметить, что макрокинетика переноса для различных нестационарных процессов во многом сходна. Аналогия различных процессов переноса массы, тепла и импульса может быть рассмотрена на примерах обработки различного вида материалов. Математическое описание нестационарной кинетики для одних процессов и материалов может быть использовано для других.

Точное описание кинетики нестационарных процессов позволяет не только обеспечить оптимальные режимы, сократить их время и, в связи с этим, снизить энергозатраты, но и повысить качественные показатели готовой продукции. Это относится к процессам переработки пищевых, химических и волокнистых материалов. Например, в таком процессе обработки волокнистых материалов, как крашение, точное знание кинетики и времени окончания процесса очень важно для получения качественного готового материала. То же самое можно сказать и для процессов переработки пищевых материалов.

Знание макрокинетики определяет возможность эффективного и экономичного проведения процессов переноса и дает возможность автоматизации управления ими. При точном знании кинетики в значительной степени решаются и проблемы энерго- и ресурсосбережения. Таким образом, точное описание кинетики процессов переноса массы и тепла является очень важным и актуальным.

Исходя из анализа литературных данных, можно отметить, что нестационарные гидродинамические, тепло- массообменные процессы многие исследователи пытаются описать либо стационарными зависимостями, разбивая процесс на периоды и под периоды, либо используют упрощенные эмпирические уравнения нестационарной кинетики. Такой подход часто вносит существенные погрешности в расчет и, как правило, не описывает предельные состояния процесса. Представляет интерес попытка рассмотрения нестационарных гидродинамических, тепло- массообменных процессов с точки зрения аналитических решений уравнения диффузии и ряда других новых экспериментальных подходов.

Важным фактором, влияющим на кинетику технологических процессов, является вид применяемых гидродинамических режимов обработки – сопловая, фильтрационная, поверхностная и др. В этом плане, важным является использование прикладных расчетов гидродинамики пограничного слоя и обтекания тел.

Важен анализ различных дисперсных структур материалов, как объектов обработки (состав пылевидных и сыпучих материалов, дисперсный состав пор в твердых телах) и их общие и частные закономерности. Этот анализ позволяет определить расчетную межфазную поверхность, рассчитать сорбционные свойства материалов, в частности определить закономерности построения изотерм сорбции-десорбции разных гигроскопичных материалов при различных температурах.

На основе решений фундаментального уравнения диффузии при условии пропорциональности коэффициента диффузии скорости распространения концентрационной волны могут быть получены новые критерии нестационарной кинетики и уравнения, описывающие ее в периоде постоянной и падающей скорости процесса. Эти уравнения, как показано, применены для описания процессов сушки плоских, волокнистых и дисперсных материалов в тонком слое, процессов сушки кусковых материалов, процессов сорбции и десорбции в газовой фазе, а также для крашения волокнистых материалов.

Использование квазистационарного метода расчета химической кинетики, развитого в работах Франка-Каменецкого для сорбционных процессов, с учетом предложенной модификации, позволяет вывести уравнения для расчета изменения концентрации, скорости, времени и коэффициентов диффузии для различных процессов сорбции-десорбции. Эти уравнения могут быть использованы в расчетах нестационарной кинетики ряда процессов химической, пищевой и текстильной промышленности, они могут быть применены, в частности, для процессов сушки и увлажнения различных химических, пищевых материалов, разных типов волокон и тканей.

Важным параметром, определяющим свойства материалов в процессе сушки, является также их усадка. В имеющихся монографиях по сушке этому параметру, как правило, уделяется сравнительно мало внимания. Особенно важно описание процесса усадки при сушке пищевых материалов, имеющих значительную начальную влажность. Эти перечисленные вопросы с конкретными примерами их расчетов, а также и ряд других рассматриваются в данной монографии.

Следует отметить, как важную особенность книги, что ряд расчетов и примеров в данной монографии с необходимыми пояснениями и программами выполнен в компьютерных средах MathCAD, MathLab и FemLab.

Глава I

Общие закономерности процессов переноса

В реальных условиях процессы переноса импульса, тепла и массы протекают как в сплошной среде (гомогенной), так и в гетерогенной системе, при наличии двух и более фаз. В случае сушки, при наличии твердой фазы процесс протекает в системе газ – твердое тело. Стационарные процессы различных видов переноса в сплошной среде изучены достаточно хорошо [1, 6, 9]. Процессы же переноса импульса, тепла и массы, протекающие в гетерогенной системе, как правило, не стационарны. Они менее изучены, т. к. нестационарность значительно усложняет описание кинетики этих процессов.

Хотя в реальных условиях возможно одновременное протекание различных видов переноса, иногда осложненное еще и химической реакцией, для изучения закономерностей переноса протекающие в промышленности процессы переноса рассматривают отдельно и классифицируют их следующим образом.

Механические – процессы механической обработки твердых материалов (основываются на законах механики твердого тела). Это процессы резания, деформации, дробления, смешения, сепарации и т. д.

Гидромеханические – процессы, описывающие движение жидкостей, газов (паров) как однофазных систем, так и многофазных, в т. ч. с взвешенными твердыми частицами. Они основываются на законах гидрогазодинамики (перенос импульса). Эти процессы описывают течения в трубах, аппаратах, каналах, насосах, компрессорах т. д.

Тепловые – процессы разного вида распространения тепла в гомогенных и гетерогенных системах, основаны на законах теплопроводности, теплообмена (перенос тепла). Эти процессы нагрева, охлаждения, конденсации, испарения т. д.

Массообменные – процессы переноса вещества в гомогенных и гетерогенных системах, основываются на законах диффузии, массообмена. Наиболее часто массообмен протекает между двумя фазами, через межфазную поверхность. Эти процессы пропитки, крашения, растворения, кристаллизации, экстракции т. д.

Химические – процессы получения новых веществ на основе протекающих химических реакций, описываются законами химической кинетики. Эти процессы получения аммиака, каучука, различных кислот, щелочей, солей, горения топлив т. д.

На практике процессы часто являются совмещенными. Так при сушке удаление влаги (массообмен) происходит обычно при нагревании материала и, следовательно, процесс тепломассооменный (перенос тепла и массы).

1.1 Закон сохранения массы

Одним из главных законов при переносе массы является закон сохранения массы. Этот закон установлен М. В. Ломоносовым. Для элементарного объема он может быть получен следующим образом.

Рис. 1.1 К выводу закона сохранения массы.

Рассмотрим поток вещества через грани элементарного объема. Плотность ρ и скорость потока u в общем случае изменяются в пространстве и во времени:

Рассмотрим изменение массы вдоль оси х (Рис. 1.1). Если проекция скорости потока на входе в элементарный объем ux, то на выходе из него, с учетом изменения на длине dx она составит:

.

Тогда изменение массы вдоль оси х за счет изменения скорости составит:

.

Аналогично определяется изменение массы вдоль остальных осей. Суммарное изменение массы, отнесенное к единице объема, вдоль всех координат должно быть равно нулю:

Выражение в скобках в уравнении (1.2) называется дивергенцией вектора скорости и обозначается div u. С учетом его получим для (1.2):

Это выражение закона сохранения массы и оно известно в гидродинамике, как уравнение сплошности, неразрывности потока. В элементарной форме это уравнение для одномерного потока, движущегося со средней скоростью v примет вид:

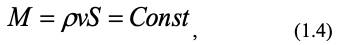
где М – массовый расход потока, S – площадь его поперечного сечения.

Для несжимаемых жидкостей (ρ = Const) уравнение (1.3) упрощается:

Для описания химического процесса в уравнении (1.2) вместо плотности подставляют массовую концентрацию компонента С. С учетом скорости образования этого компонента по химической реакции r, если она имеет место, для уравнения (1.2) получим:

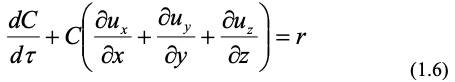
С учетом, что концентрация компонента изменяется в пространстве и во времени, получим:

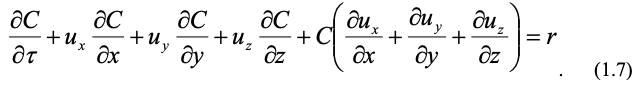
В частном случае для стационарных процессов первый член в левой части уравнения (1.6) равен нулю, а в случае отсутствия химической реакции правый член этого уравнения также равен нулю.

1.2 Закон сохранения количества движения

В движущемся потоке газа или жидкости действуют массовые и поверхностные силы. Они оказывают влияние на взаимодействие, соударения молекул, что обуславливает перенос количества движения. По второму закону Ньютона изменение количества движения в единицу времени (импульс) численно равно силе:

Поэтому баланс сил в движущемся потоке представляет собой закон сохранения количества движения (импульса).

Рис. 1.2 К выводу закона сохранения количества движения.

Рассмотрим равновесие сил в движущемся потоке в проекциях на ось х (Рис. 1.2). На правую и левую грани действуют силы давления. Их проекция на ось х составит –

.

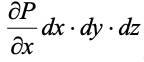
Проекция массовой силы Q на ось х запишется:

.

На верхнюю и нижнюю грани действуют силы вязкостного трения. Их проекция на ось х составит .

С учетом закона Ньютона для вязкостного трения:

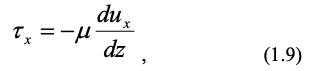
имеем проекцию сил вязкостного трения на ось х:

.

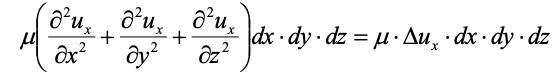
Здесь выражение в скобках – оператор Лапласа от проекции скорости на ось х, он обозначается Δu_x или ²u_x.

Так как сумма проекций всех сил равна проекции силы инерции:

,

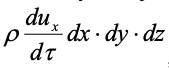
относя все силы к единице объема, получим:

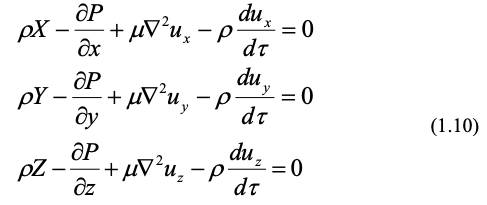
Последние два уравнения получены аналогично для осей у и z, а в целом система уравнений (1.10) в гидрогазодинамике называется уравнениями движения вязкой жидкости Навье-Стокса и выражает закон сохранения количества движения.

Система уравнений Навье-Стокса может быть записана более детально, если раскрыть полную производную проекции скорости. Так уравнение для оси х, например, при делении всех его членов на ρ , c учетом, что ν = μ/ρ, будет иметь вид:

.

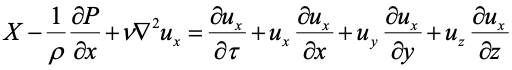
Аналогично записываются уравнения для осей у и z.

1.3 Закон сохранения энергии

Рассмотрим сначала закон сохранения энергии для движения идеальной жидкости. Так как в идеальной жидкости отсутствуют силы вязкостного трения, то для этого случая из системы уравнений (1.10), положив проекции силы вязкости равным нулю, получим следующую систему (система уравнений движения идеальной жидкости Эйлера):

.

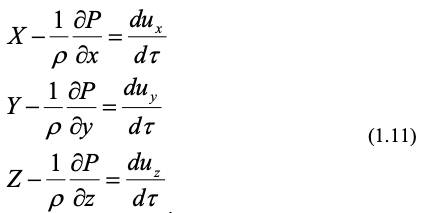
Помножим эти уравнения соответственно на dx, dy, dz и сложим. Тогда, преобразуя, получим следующее уравнение:

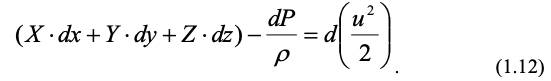
В поле силы тяжести (Х = 0; У = 0; Z = – g) уравнение (1.12) примет вид:

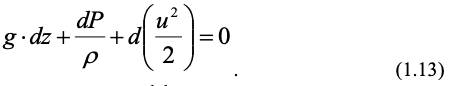
Это уравнение определяет в дифференциальном виде закон сохранения энергии для движения идеальной жидкости и представляет собой, соответственно, сумму удельных (отнесенных к единице массы) потенциальных энергий положения и давления и кинетической энергии. При интегрировании уравнения (1.13) для потока несжимаемой жидкости (ρ = Const) получим уравнение Бернулли для одномерного потока, движущегося со средней скоростью v:

Уравнение Бернулли показывает, что для идеальной жидкости сумма потенциальной и кинетической энергий остается постоянной вдоль всего потока.

В более общей форме закон сохранения энергии описывает 1-й закон термодинамики: теплота, подводимая к системе, идет на производство работы и увеличение энергии системы:

Выражение для потока энергии в дифференциальном виде включает ее члены, входящие в уравнение (1.13) плюс, внутренняя энергия dU. С учетом этого запишем уравнение (1.15) в следующем виде:

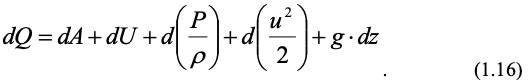
Сумма второго и третьего членов правой части уравнения (1.16) представляет собой изменение энтальпии dh. С учетом этого получим другой вид уравнения (1.16):

1.4 Микро- и макроперенос

Молекулярный перенос, называемый еще микропереносом, происходит вследствие беспорядочного теплового движения микрочастиц (броуновское движение), когда среда в целом неподвижна. Перенос массы при наличии молекулярного переноса называется молекулярной диффузией. Перенос тепла под действием молекулярного переноса называется теплопроводностью. Перенос количества движения под действием молекулярного переноса происходит при наличии молекулярного (вязкостного) трения при ламинарном движении среды. Процесс микропереноса описывается микрокинетикой.

Примером микропереноса массы может служить диффузия капли красителя, чернил в сосуде с водой, происходящая вследствие теплового движения молекул воды. В процессе переноса массы в сосуде создаются поля концентрации красителя. Эти поля изменяются во времени (микрокинетика) до момента равномерного распределения концентрации красителя по всему объему. Процесс в зависимости от свойств и параметров (объем, температура) системы может занять от долей секунды до нескольких часов и даже суток. Движущей силой переноса в этом случае является разность концентраций красителя в разных точках объема. Поля концентраций в этом случае не стационарны. Достижение момента равномерного распределения концентрации красителя соответствует состоянию материального равновесия (постоянства состава по объему).

В качестве примера микропереноса тепла можно рассмотреть процесс теплопереноса при погружении нагретого шара в сосуд с жидкостью. Микроперенос обеспечивается теплопроводностью жидкости и шара. Поле температур изменяется во времени до момента установления равенства температур в погруженном теле и в жидкости. Движущей силой переноса в этом случае является разность температур в разных точках объема. Поле температур как в теле, так и в жидкости не стационарно. Достижение момента равномерного распределения температур соответствует состоянию теплового равновесия (постоянства температуры во всем объеме).

Примером микропереноса количества движения, происходящего вследствие наличия молекулярного (вязкостного) трения при ламинарном движении среды может служить осаждение малых частиц в жидкости. При осаждении скорость частицы возрастает от нуля до конечного значения, обусловленного равновесием сил, действующих на частицу – тяжести, архимедовой и сопротивления среды. Движение частицы в этом случае описывается законом Стокса. Движущей силой переноса в этом случае является разность скоростей. Движение частицы в начальный период не стационарно. При достижении постоянной скорости осаждения (сила инерции частицы равна нулю) достигается постоянство распределения скоростей (эпюры скоростей) при осаждении частицы. Движение частицы становится стационарным.

Макроперенос – это перенос определенных объемов массы, перенос энергии этих объемов, перенос количества движения, которым обладают эти объемы. Макроперенос обусловлен наличием конвекции (свободной или вынужденной), вихреобразованиями. Кинетика процесса макропереноса называется макрокинетикой.

Рассмотренные выше примеры микропереноса могут быть реализованы в условиях макропереноса. Так для ускорения диффузии красителя в сосуде с водой необходимо использовать перемешивание. Возникающие при этом циркуляционные токи значительно быстрее, чем при микропереносе, выровняют концентрацию красителя по всему объему.

В примере с теплопереносом от нагретого шара к жидкости, для интенсификации процесса также достаточно применить перемешивание. Конвективный макроперенос тепла протекает значительно быстрее, чем перенос теплопроводностью.

Макроперенос количества движения происходит, например, при осаждении крупных частиц в турбулентном режиме за счет образования турбулентных завихрений. Движение частицы в этом случае описывается законом Ньютона.

При макропереносе имеет место также и микроперенос, однако интенсивность последнего намного ниже. При движении среды макроперенос, как правило, превалирует по сравнению с микропереносом. Именно поэтому макрокинетика наиболее важна, как определяющая все виды процессов переноса – переноса массы, энергии и количества движения или импульса.