Джордан Элленберг
Форма реальности

Во введении в «Изобретательную геометрию» говорится, что геометрия имеет «место в образовании всех людей, не исключая женщин»: автор книги, Уильям Джордж Спенсер, – один из первых поборников совместного обучения. Более типичное отношение к женщинам и геометрии в XIX веке отражено (но не одобряется) в романе «Мельница на Флоссе» Джорджа Элиота^[42], опубликованном в том же году, что и учебник Спенсера. «Девчонки не могут понять Евклида, правда, сэр?» – спрашивает один из персонажей учителя Стеллинга, на что тот отвечает: «У них иногда неплохие способности, но знания их неглубоки, они ничего не могут постичь до конца. Они смышленые, но поверхностные»^[43]. Стеллинг представляет в сатирической форме тот традиционный образ британской педагогики, против которого восставал Спенсер: долгий марш через запоминание авторитетов, при котором медленный и тяжелый строительный процесс понимания не просто игнорируют, его остерегаются. «Мистер Стеллинг был не из тех, кто станет ослаблять и изнеживать ум своего питомца, прибегая к упрощениям и объяснениям»^[44]. Евклид был своего рода тонизирующим средством для укрепления мужественности, и его приходилось терпеть, как крепкий напиток или ледяной душ.

Недовольство стеллингизмом стало нарастать даже в верхах математических кругов. Британский математик Джеймс Джозеф Сильвестр, о геометрии и алгебре (а также отвращении к отупляющей мертвенности британской академической науки) которого мы еще поговорим, считал, что Евклида нужно спрятать «подальше от школьников», а геометрию преподавать в связке с физикой, делая акцент на геометрию движения, дополняющую статические формы Евклида. «Именно живого интереса^[45] к предмету, – писал Сильвестр, – так не хватает нашим традиционным средневековым методам преподавания. Во Франции, Германии и Италии – везде, где я был на континенте, – разум воздействует непосредственно на разум: тем способом, который неизвестен застывшей формалистике наших академических учреждений».

СМОТРИ!

Мы уже не заставляем школьников заучивать и повторять наизусть Евклида. В конце XIX века в учебники стали включать упражнения, в которых ученикам предлагалось строить собственные доказательства геометрических утверждений. В 1893 году эти перемены узаконил сформированный в 1892-м Комитет десяти, возглавляемый президентом Гарварда Чарльзом Элиотом. Комитету было поручено рационализировать и стандартизировать обучение в американских средних школах. По его утверждению, задача геометрии в школе – прививать ученикам навыки строгого дедуктивного мышления. Эта идея прижилась. В ходе опроса пятисот американских учителей об их задачах в преподавании геометрии, проведенного в 1950 году^[46], самым популярным был ответ: «Развить навыки ясного мышления и точного выражения», который почти вдвое превысил вариант: «Дать знание фактов и принципов геометрии». Иными словами, мы здесь не для того, чтобы пичкать учеников всеми известными фактами о треугольниках, а для того, чтобы развивать в них умственную дисциплину, позволяющую добывать эти факты из первоначальных принципов. Школа для маленьких Линкольнов.

А для чего нужна эта умственная дисциплина? Может быть, на случай, если в какой-то момент будущей жизни им понадобится окончательно и неопровержимо доказать, что сумма внешних углов многоугольника равна 360 градусам? Я все жду, когда же это произойдет, но пока безрезультатно.

Основная причина обучения детей формулированию доказательств вовсе не в том, что мир полон доказательств, а в том, что мир полон недоказательств, и взрослым людям нужно знать разницу. Трудно согласиться с недоказательством, если вы реально знакомы с подлинником.

Линкольн понимал эту разницу. Его друг и коллега-юрист Генри Клей Уитни вспоминал: «Много раз я видел^[47], как он срывает маску с заблуждения и стыдит как заблуждение, так и его автора». Мы постоянно встречаемся с недоказательствами, рядящимися в одежду доказательств, и без должного внимания с нашей стороны они часто обходят нашу защиту. Существуют подсказки, которые вы можете высматривать. Когда в математике какой-то автор начинает фразу со слов «Очевидно, что», на самом деле он говорит: «Мне это кажется очевидным. Вероятно, следовало бы это проверить, но я немного запутался в процессе и потому решил просто заявить, что это очевидно». У газетных аналитиков аналогичная фраза начинается со слов: «Конечно, все мы согласны с тем, что». Всякий раз, сталкиваясь с подобным, вы ни в коем случае не должны верить, что все согласны с дальнейшим. Вас просят трактовать нечто как аксиому, но если мы что-то и обязаны выучить из истории геометрии, так это то, что нельзя включать аксиому в свою книгу, пока она не доказала свою реальную ценность.

Всегда скептично относитесь к любому, кто говорит, что он «просто логичен». Если вам рассказывают не о равенстве треугольников, а об экономической политике, или о каком-то недостойно себя ведущем культурном деятеле, или об уступке, которую от вас хотят, то тут нет ничего «просто логичного», поскольку все происходит в контексте, где логические выводы – если они вообще применимы – неотделимы от всего остального. От вас хотят, чтобы вы ошибочно приняли цепочку уверенно выраженных мнений за доказательство. Но как только вы ощутите резкий щелчок настоящего доказательства, вы уже никогда не угодите в эту ловушку. Предложите своему «логичному» оппоненту заняться квадратурой круга.

По словам Уитни, Линкольн выделялся вовсе не сверхмощным интеллектом. Многие общественные деятели очень умны, но среди них есть и хорошие, и плохие люди, с сожалением отмечает Уитни. Линкольна же отличало то, что для него «было морально невозможно^[48] спорить нечестно; он не мог этого делать по определению, как не мог красть; по сути, для него было одно и то же – лишить человека собственности путем кражи или путем нелогичных или отвратительных рассуждений». То, что Линкольн позаимствовал у Евклида (или то, что уже имелось у Линкольна и гармонировало с тем, что он нашел у Евклида), – это целостность: принцип, что нельзя говорить какие-то вещи, пока ты честно не обосновал свое право их обсуждать. Геометрия – это форма честности. Линкольна можно назвать Геометрическим Эйбом^[49].

Единственное, в чем я расхожусь с Линкольном, – что он стыдит автора за заблуждения. Труднее всего быть честным с самим собой, и требуется гораздо больше времени и усилий на разоблачение собственных ошибок. Нужно всегда относиться к своим убеждениям, как к расшатанному зубу, то есть к зубу, в крепости которого вы не совсем уверены. И если что-то вызывает сомнения, не стоит стыдиться; просто спокойно отступите на твердую почву и заново переосмыслите проблемное понятие.

Именно этому в идеале должна научить нас геометрия. Однако «застывшая формалистика», на которую жаловался Сильвестр, от этого ой как далека. На практике урок геометрии, который мы преподаем детям, по словам художника, педагога и популяризатора математики Бена Орлина, обычно таков:

Доказательство – это непонятная демонстрация уже известного вам факта^[50].

Орлин приводит пример такого доказательства для теоремы о равенстве прямых углов, то есть утверждения, что любые два прямых угла равны. Что можно спросить у девятиклассника, столкнувшегося с этим утверждением? Типичный формат^[51] – доказательство в два столбца, главная опора геометрического образования в течение более чем ста лет. В нашем случае оно выглядело бы примерно так:

«Транзитивность равенства» – одно из общих понятий Евклида, это арифметический принцип, который он излагает в начале своего труда наряду с геометрическими аксиомами. Принцип таков: две вещи, равные третьей, равны между собой^[52].

Не стану отрицать, что есть определенное удовлетворение в сведении всего к таким крошечным, точным шагам. Они так убедительно складываются вместе, словно детальки лего! И подобное ощущение учителю действительно хочется передать.

Но все же… разве не очевидно, что два прямых угла – это одна и та же вещь, просто расположенная на странице в разных местах с разной ориентацией? На самом деле Евклид считал равенство прямых углов четвертой из аксиом – основных правил игры, которые принимаются как истинные без доказательства и из которых вытекает все остальное. Так почему современная школа требует от учеников предъявлять доказательство этого факта, если даже Евклид сказал: «Да ладно, это очевидно»? Потому что существует много разных наборов аксиом, из которых можно вывести геометрию на плоскости, и поступать в точности так, как Евклид, больше не считается самым строгим или педагогически выигрышным приемом. В 1899 году Давид Гильберт переписал всю аксиоматику с нуля, а аксиомы современной американской школы обычно следуют системе Джорджа Биркгофа 1932 года.

Аксиома это или нет, но тот факт, что два прямых угла равны, ученик просто знает. Вы не можете винить школьников в том, что они разочаруются, когда вы им скажете: «Вы думали, что знаете это, но на самом деле не знали, пока не выполнили все шаги в доказательстве в два столбца». Даже несколько обидно!

Слишком многое на уроках геометрии посвящено доказательству очевидных вещей. Я хорошо помню занятия топологией на первом курсе колледжа. Профессор, весьма выдающийся почтенный ученый, потратил две недели на доказательство следующего факта: если вы проведете на плоскости замкнутую кривую без самопересечений, то, какой бы извилистой и причудливой она ни была, она разделит плоскость на две части: одна внутри, а вторая – снаружи кривой.

С одной стороны, как оказалось, весьма сложно написать формальное доказательство этого факта, известного как теорема Жордана о замкнутых кривых. С другой – эти две недели я провел в состоянии едва сдерживаемого раздражения. Неужели в этом и заключается математика? Делать очевидное трудоемким? Читатель, я просто отключался, так же как и мои однокурсники, среди которых были будущие математики и другие ученые. Парочка, сидевшая передо мной, – весьма серьезные студенты, которые впоследствии получат степени по математике в лучших университетах, – начинала энергично обниматься всякий раз, когда выдающийся почтенный ученый поворачивался к доске, чтобы записать очередной тонкий аргумент о небольшом видоизменении многоугольника. Я имею в виду, что они реально заводились, как будто их подростковая страсть друг к другу могла каким-то образом перенести их в другую часть континуума, где такого доказательства еще нет.

Столь высококвалифицированный математик, каким я стал сейчас, мог бы, слегка выпрямившись, сказать: «Ну, молодые люди, вы просто недостаточно искушены, чтобы понимать, какие утверждения действительно очевидны, а какие скрывают в себе тонкости». Возможно, я упомянул бы пугающую рогатую сферу Александера^[53], которая показывает, что аналогичный вопрос в трехмерном пространстве вовсе не так прост, как можно подумать^[54].

Однако с педагогической точки зрения такой ответ, на мой взгляд, довольно плох. Если в классе мы будем тратить время на доказательство вещей, которые кажутся очевидными, и настаивать на том, что они неочевидны, наши ученики будут кипеть от возмущения, как когда-то я, или найдут себе занятия поинтереснее, когда преподаватель отвернется.

Мне нравится, как мастер преподавания Бен Блюм-Смит описывает эту проблему: чтобы учащиеся действительно ощутили огонь математики, им надо испытать градиент уверенности^[55], ^[56] – ощущение перехода от чего-то очевидного к чему-то неочевидному, подталкиваемое вверх двигателем формальной логики. В противном случае мы говорим: «Вот список аксиом, которые выглядят совершенно правильными; складывайте их, пока не получите другое утверждение, которое выглядит совершенно правильным». Это все равно что обучать кого-нибудь лего, показав, что из двух маленьких кирпичиков можно сделать один большой. Вы можете это сделать, а иногда вам действительно нужно это сделать, но суть лего, конечно, не в этом.

Вероятно, лучше самому почувствовать градиент уверенности, чем говорить о нем. Для этого подумайте на миг о прямоугольном треугольнике.

Начнем с интуитивного ощущения: если горизонтальная и вертикальная стороны определены, то известна и диагональ. Если вы пройдете 3 километра на юг, а потом 4 километра на восток, то однозначно удалитесь от исходной точки на какое-то конкретное расстояние.

Но на какое? Для этого нужна теорема Пифагора – первая реальная теорема геометрии. Она говорит, что если a и b – горизонтальная и вертикальная стороны прямоугольного треугольника, а c – диагональ (так называемая гипотенуза), то

a² + b² = c².

Если a = 3, а b = 4, то c² = 3² + 4² = 9 + 16 = 25. Мы знаем, какое число при возведении в квадрат дает 25: это число 5. Оно и есть длина гипотенузы.

Почему эта формула верна? Вы можете начать подниматься по градиенту уверенности, нарисовав треугольник со сторонами 3 и 4 и измерив его гипотенузу, она будет близкой к 5. Затем нарисуйте треугольник со сторонами 1 и 3 и измерьте его гипотенузу; если вы обращались с линейкой достаточно внимательно, то получите что-то близкое к числу 3,16, которое при возведении в квадрат дает 1 + 9 = 10. Благодаря этим примерам уверенность увеличится, но это еще не доказательство. А вот это уже оно:

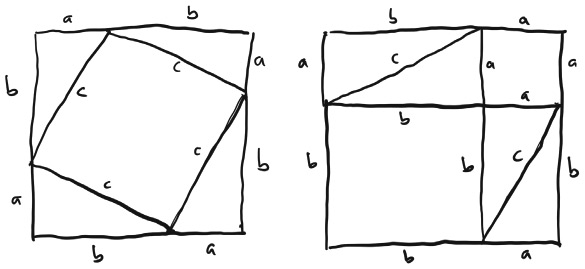
Большой квадрат на обоих рисунках одинаков, но разбит на части двумя разными способами. На первом чертеже четыре копии нашего прямоугольного треугольника и квадрат со стороной c. На втором – тоже четыре копии, но иначе расположенные: остаток квадрата теперь занимают два меньших квадрата со сторонами a и b. Площадь, которая остается в большом квадрате после убирания четырех треугольников, должна быть одинаковой в обоих случаях, а значит, c² (площадь, оставшаяся на первом чертеже) будет равна a² + b² (площадь, оставшаяся на втором чертеже).

При желании придраться можно пожаловаться на нестрогое доказательство того, что на первом рисунке квадрат (того, что длина сторон этой фигуры одинакова, недостаточно: сожмите пальцами противоположные углы квадрата – и получите фигуру под названием ромб: это явно не квадрат, но стороны по-прежнему равны). Но пусть так. До ознакомления с этой иллюстрацией у вас нет оснований считать, что теорема Пифагора верна, но, увидев ее, вы поймете, почему теорема верна. Подобные доказательства, когда геометрическая фигура разрезается на части, которые потом переставляются, называются доказательствами разрезания и ценятся за ясность и изобретательность. Математик и астроном XII века Бхаскара^[57] показывает такую форму доказательства теоремы и находит изображение настолько убедительным, что для него не требуется словесное пояснение, просто подпись в виде одного слова «Смотри!»^[58]. Любитель-математик Генри Перигал в 1830 году придумал собственное доказательство разрезанием, когда пытался, подобно Линкольну, квадрировать круг; он настолько высоко ценил свою схему^[59], что спустя почти шестьдесят лет завещал вырезать ее на своем надгробии.

ЧЕРЕЗ МОСТ ОСЛОВ

Нам нужно знать, как решать геометрические задачи чисто формальными выводами, однако геометрия – это не просто последовательность чисто формальных выводов. Если бы это было так, то это был бы не лучший способ научить искусству систематических рассуждений в сравнении с тысячей других вещей. Мы могли бы объяснять шахматные задачи или судоку. Или создать систему аксиом, вообще не имеющую никакого отношения к какой-либо области человеческой деятельности, и заставлять учащихся выводить из нее следствия. Но вместо всего этого мы преподаем геометрию, поскольку она – формальная система, которая не просто формальная система. Она встроена в наши представления о пространстве, положении и движении. Мы не можем не быть геометрическими. Иными словами, у нас есть интуиция.

В эссе 1905 года геометр Анри Пуанкаре определил интуицию и логику как два незаменимых столпа математического мышления. Каждый математик склонен к той или иной стороне, и, как отмечает Пуанкаре, нам свойственно именовать геометрами тех, кто сильнее предрасположен к интуитивному мышлению. Нам нужны оба столпа. Без логики мы не могли бы ничего сказать о 1000-угольнике – объекте, который нам не представить ни в каком разумном смысле. Но без интуиции предмет теряет всю свою привлекательность. Пуанкаре объясняет, что Евклид – это мертвая губка:

Вы, несомненно, видели^[60] те тонкие структуры кремниевых игл, которые формируют скелет некоторых губок. Когда органическая материя исчезает, остается только хрупкое и изящное кружево. Правда, там нет ничего, кроме оксида кремния, но интересна именно та форма, которую он принял, и мы не могли бы ее понять, если бы не знали живой губки, которая и придала ему такую форму. Именно так и старые интуитивные представления наших отцов – даже тогда, когда мы отказались от них, – все еще придают форму логическим построениям, которые пришли им на смену.

Каким-то образом нам нужно научить людей делать выводы, не отрицая наличия интуитивных способностей – той самой живой ткани губки. И все же мы не хотим, чтобы нами управляла исключительно интуиция. Здесь поучительна история постулата о параллельных. Евклид включил его в список аксиом: «Если дана прямая L и точка P вне ее, то через точку P можно провести одну и только одну прямую, параллельную прямой L»^[61].

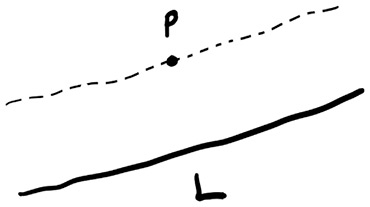
Это сложно и громоздко по сравнению с другими аксиомами, которые выглядят изящнее, например: «Через любые две точки можно провести прямую». Математикам казалось, что было бы лучше, если бы получилось вывести пятую аксиому из четырех других, которые считались более базовыми.

Но зачем? Ведь наша интуиция громко кричит, что пятая аксиома верна. Что может быть бесполезнее, чем пытаться это доказать? Это все равно что спрашивать, можем ли мы доказать, что 2 + 2 = 4. Мы это знаем!

И все же математики упорствовали, раз за разом безуспешно пытаясь показать, что пятая аксиома выводится из остальных. В итоге оказалось, что усилия изначально были обречены на неудачу, потому что существуют и другие геометрии, в которых прямая, точка и плоскость означают вовсе не то, что подразумевал под этими словами Евклид (и, вероятно, вы), однако они удовлетворяют первым четырем аксиомам, но не удовлетворяют пятой. В некоторых из этих геометрий через точку P проходило бесконечно много прямых, параллельных прямой L. В других не было ни одной такой прямой.

Нет ли тут обмана? Мы же не спрашиваем о каких-то геометрических сущностях других странных миров, которые извращенно называем прямыми. Мы говорим о настоящих прямых, для которых пятый постулат Евклида, безусловно, верен.

Да, конечно, вы можете пойти этим путем. Но, поступая таким образом, сознательно закроете себе доступ к целому миру геометрий просто потому, что это не та геометрия, к которой вы привыкли. Неевклидова геометрия – фундамент для обширных областей математики, включая и ту, что описывает физическое пространство, в котором мы реально живем. (Мы вернемся к этому вопросу через несколько страниц.) Мы могли бы отказаться открывать ее на основании своего жесткого евклидова пуризма. Но это была бы наша потеря.

Вот еще один пример, требующий нахождения баланса между формальной логикой и интуицией. Предположим, у нас есть равнобедренный треугольник, то есть его стороны AB и AC равны. Теорема: углы B и C тоже равны.

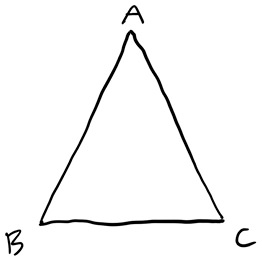
Это утверждение иногда называют pons asinorum, то есть мост ослов, потому что это штука, через которую почти всех нас нужно осторожно провести. Здесь доказательство Евклида поважнее, чем вышеописанная ситуация с прямыми углами. Мы сразу оказываемся in medias res^[62], хотя в школе подходили к мосту ослов только после нескольких недель подготовки. Поэтому примем как данность Предложение 4 книги I Евклида, где говорится, что если вы знаете две стороны треугольника и угол между ними, то можете найти длину третьей стороны и два оставшихся угла. Иными словами, если я нарисую так:

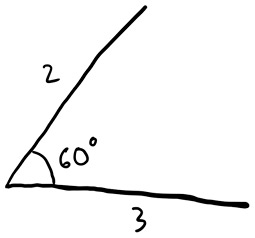
то существует только один способ восстановить оставшуюся часть треугольника. Другой способ сказать то же самое: если у двух треугольников равны две пары сторон и углы между ними, то у них равны все углы и все стороны, то есть, как говорят геометры, треугольники равны, или конгруэнтны.

Мы уже обращались к этому факту, когда угол между двумя сторонами был прямым, но я думаю, что и в случае произвольного угла это кажется столь же понятным.

(Кстати, справедливо и следующее: если три стороны двух треугольников равны, то и треугольники равны; например, если длины сторон 3, 4 и 5 равны, то треугольник должен быть прямоугольным, как я нарисовал выше. Однако это менее очевидно, что Евклид и доказал несколько позднее: Предложение I.8. Если вам кажется, что это очевидно, подумайте о четырехугольнике: вспомните ромб, с которым мы недавно встречались, – у него такие же стороны, как у квадрата, но он же не квадрат.)

А теперь перейдем к pons asinorum. Доказательство в два столбца может выглядеть так:

^[63]

Да, мы посреди доказательства, но у нас новая точка и новый отрезок AD, так что лучше обновить чертеж! Кстати, вспомните, что, по нашему предположению, треугольник равнобедренный, поэтому длина AB и AC одинакова; сейчас мы это используем.

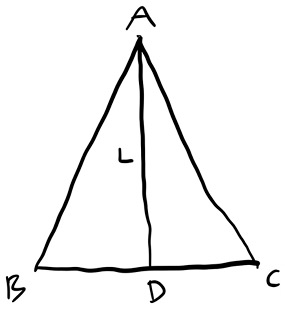
QED^[64].

Это доказательство посерьезнее, чем то, что мы видели, поскольку тут вам действительно приходится что-то делать: вы проводите новую линию L и придумываете название D для точки, где L пересекает BC. Это позволяет вам воспринять точки B и C как углы двух новых треугольников ABD и ABC, которые, как мы продемонстрируем далее, равны.

Однако существует и более хитрый способ, изложенный примерно через шестьсот лет после Евклида Паппом Александрийским, еще одним геометром из Северной Африки, в трактате Συναγωγή («Математическое собрание»). (Слово «синагога» означает «собрание», и в античном мире оно могло обозначать собрание математических предложений, а вовсе не собрание евреев на молитву.)

Погодите, что произошло? Казалось бы, мы ничего не делали, а нужное заключение появилось просто из ниоткуда, как кролик, выпрыгивающий при отсутствии шляпы. Это создает определенное беспокойство. Это не то, что понравилось бы Евклиду. Но так или иначе, на мой взгляд, это верное доказательство.

Ключ к идее Паппа – предпоследняя строка: треугольники BAC и CAB конгруэнтны. Кажется, что это просто утверждение о равенстве треугольника самому себе, которое выглядит тривиальным. Но присмотритесь более внимательно.

Что на самом деле мы имеем в виду, говоря, что два разных треугольника PQR и DEF конгруэнтны?

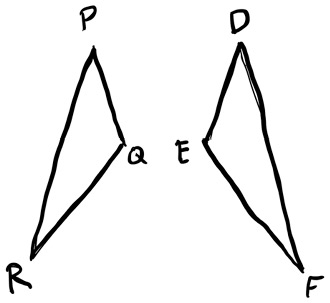
А вот что! Мы утверждаем сразу шесть вещей: длина PQ равна длине DE, длина PR равна длине DF, длина QR равна длине EF, угол P равен углу D, угол Q равен углу E, угол R равен углу F.

Конгруэнтен ли треугольник PQR треугольнику DFE? Нет, потому что на рисунке длина стороны PQ не равна длине соответствующей стороны DF.

Если мы серьезно воспринимаем определение конгруэнтности (а для нас, геометров, принимать определения всерьез – в некотором роде фирменная фишка), то треугольники DEF и DFE не конгруэнтны, несмотря на то что это один и тот же треугольник. Потому что DE и DF имеют разную длину.

Однако в нашем доказательстве с мостом ослов треугольник равнобедренный, а потому, когда мы воспринимаем его как треугольник BAC, он в точности тот же, что и в случае, когда мы его рассматриваем как треугольник CAB. Это не тривиальное утверждение. Если я говорю, что имя АННА читается одинаково в обоих направлениях, я в действительности сообщаю вам тот факт, что это палиндром. Возражать против самой концепции палиндрома, заявляя: «Ну конечно, это одно и то же, там две буквы А и две буквы Н, а порядок не важен», – чистое извращение.

На деле слово «палиндромный» было бы хорошим названием для треугольников типа BAC, который конгруэнтен треугольнику CAB, получаемому при записи вершин в обратном порядке. Именно благодаря такой идее Папп и сумел пройти через мост, не прибегая к дополнительным линиям и точкам.

И все же доказательство Паппа не вполне объясняет, почему равнобедренный треугольник имеет два равных угла. Представление о палиндромности равностороннего треугольника, то есть о том, что он остается таким же при записи вершин в обратном порядке, говорит вам то же, что (я уверен) и ваша интуиция: треугольник остается неизменным, когда вы берете его, переворачиваете и кладете обратно на то же место. Как и слово-палиндром, он обладает симметрией. Вот почему нам кажется, что углы должны быть равны.

На уроках геометрии нам обычно не разрешают говорить о переворачивании фигур^[65], хотя делать это нужно. С какими бы абстракциями мы ни имели дело, математика – это то, чем мы занимаемся с помощью нашего тела. И прежде всего – геометрия. Иногда буквально: каждый математик обнаруживал, что рисует невидимые фигуры с помощью жестов, и как минимум одно исследование^[66] показало, что дети, которым предлагали представить геометрическую задачу в движениях, чаще приходили к верному заключению^[67]. Говорят, сам Пуанкаре в геометрических рассуждениях полагался на свое чувство движения. Он не был визуалом и плохо запоминал лица и фигуры, поэтому, когда ему требовалось^[68] нарисовать картинку по памяти, он, по его словам, вспоминал не то, как она выглядела, а то, как по ней двигался его взгляд.

РАВНОБЕДРЕННОСТЬ

Что означает слово «равнобедренный» в названии треугольников? Прежде всего то, что две его стороны равны. В греческом языке используется слово σκέλη (скеле), что значит «ноги», отсюда и английское isosceles. В китайском слово 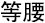составлено из иероглифов равный и талия, на русском языке у такого треугольника равные бедра, а на иврите – равные голени. В любом случае мы, похоже, согласны с тем, что быть равнобедренным означает иметь две равные стороны. Но почему? Почему бы не определить равнобедренный треугольник как треугольник, у которого равны два угла? Вы, вероятно, заметили (а весь смысл pons asinorum в том, чтобы это доказать!), что равенство двух сторон означает равенство двух углов, и наоборот. Другими словами, эти два определения эквивалентны и задают одно и то же множество треугольников. Но я бы не сказал, что это одно и то же определение. Существуют и другие варианты. Более современно было бы определить равнобедренный треугольник как палиндромный: треугольник, который вы можете взять, перевернуть, положить обратно, и он при этом не изменится. То, что у такого треугольника будут две равные стороны и два равных угла, следует почти автоматически. В этом геометрическом мире рассуждение Паппа показывало бы, что треугольник с двумя равными сторонами равнобедренный, а треугольники BAC и CAB совпадают.

Хорошее определение – то, которое проливает свет на ситуации, выходящие за рамки того, для чего оно было придумано. Идея, что равнобедренный означает не изменяющийся при переворачивании, дает нам хорошее представление о том, что такое равнобедренная трапеция или равнобедренный пятиугольник. Вы могли бы сказать, что равнобедренный пятиугольник – тот, у которого две стороны равны, но тогда вы соглашаетесь на перекошенные обвисшие пятиугольники наподобие этого:

Но хотите ли вы этого? К определению «равнобедренный» явно лучше подходит вот такой симпатичный пятиугольник:

И в самом деле, в школьном учебнике равнобедренная трапеция – это не фигура с двумя равными сторонами или двумя равными углами, а фигура, которую можно перевернуть, и она не изменится. Сюда прокралось постевклидово понятие симметрии, потому что наши мозги устроены так, что его замечают. Все чаще и чаще идея симметрии становится основанием для доказательств на уроках геометрии. Это не Евклид, но именно такова сейчас геометрия.