Яков Перельман
Загадки и диковинки в мире чисел

Полная версия

Арифметические ребусы

Арифметические ребусы – занимательная игра американских школьников, у нас пока еще совершенно неизвестная^[6]. Она состоит в отгадывании задуманного слова посредством решения задачи вроде той, какую мы сейчас решили в статье «Арифметика за завтраком». Загадывающий задумывает слово, состоящее из 10 неповторяющихся букв – например, «трудолюбие», «специально», «просвещать». Приняв буквы задуманного слова за цифры, загадывающий изображает посредством этих букв какой-нибудь случай деления. Если задумано слово «просвещать», то можно взять такой пример деления:

Можно взять и другие слова для делимого и делителя – например:

Буквенное изображение того или иного случая деления вручается отгадчику, который и должен по этому бессмысленному, казалось бы, набору букв угадать задуманное слово. Как в подобных случаях следует доискиваться числового значения букв, – читатель уже знает: мы объяснили это, когда решали задачу, предложенную в предыдущей статье. При некотором терпении всегда можно успешно разгадывать эти арифметические ребусы, если только пример достаточно длинен и дает необходимый материал для догадок и испытаний. Если же выбраны слова, дающие чересчур короткий случай деления, например:

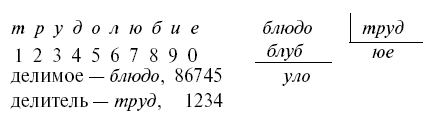
– то разгадывание очень трудно. В подобных случаях надо просить загадывающего продолжить деление до сотых или тысячных долей, т. е. получить в частном еще 2 или 3 десятичных знака. Вот пример деления до сотых долей:

Если бы в этом случае мы остановились на целом частном (со), отгадка задуманного слова едва ли была бы возможна.

Для читателя, который пожелал бы испытать свои силы в разрешении подобных арифметических ребусов, привожу еще несколько примеров:

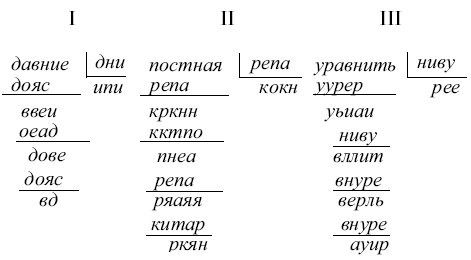
По этим образцам читатель сможет самостоятельно подыскать множество других примеров.

Десятичная система в книжных шкафах

Особенность десятичной системы счисления остроумно используется даже в области, где с первого взгляда этого и ожидать не приходится, – именно, при распределении книг в библиотеке.

Обычно, желая указать библиотекарю номер нужной вам книги, вы просите дать вам каталог и предварительно справляетесь в нем, – потому что в каждом книгохранилище существует обыкновенно своя нумерация книг. Однако имеется и такая система распределения книг по номерам, при которой одна и та же книга должна иметь одинаковый номер во всякой библиотеке. Это так называемая десятичная система классификации книг.

Система эта – к сожалению, принятая пока еще далеко не всюду, – чрезвычайно удобна и весьма не сложна. Сущность ее состоит в том, что каждая отрасль знания обозначается определенным числом и притом так, что цифровой состав этого числа сам говорит о месте данного предмета в общей системе знаний.

Книги прежде всего разбиваются на десять обширных классов, обозначенных цифрами от 0 до 9.

0. Сочинения общего характера.

1. Философия.

2. Религия.

3. Общественные науки.

4. Филология.

5. Физико-математические и естественные науки.

6. Прикладные науки.

7. Изящные искусства.

8. Литература.

9. История и география.

В обозначении номера книги по этой системе первая цифра прямо указывает на ее принадлежность к определенному классу из перечисленных выше: каждая книга по философии имеет номер, начинающийся с 1, по математике – с 5, по технике – с 6. И наоборот, если номер книги начинается, например, с 4, то мы, не раскрывая книги, можем утверждать, что перед нами сочинение из области языкознания.

Далее, каждый из десяти перечисленных классов книг подразделяется на 10 главных отделов, тоже отмеченных цифрами; эти цифры ставят в обозначении номера на втором месте. Так, 5-й класс, включающий физико-математические и естественные книги, разделяется на следующие отделы:

50. Общие сочинения по физико-математическим и естественным наукам.

51. Математика.

52. Астрономия. Геодезия.

53. Физика. Механика.

54. Химия.

55. Геология. Палеонтология.

56. Общая география.

57. Биология. Антропология.

58. Ботаника.

59. Зоология.

Сходным образом разбиваются по отделам и остальные классы. Например, в классе прикладных наук (6) отдел медицины обозначается цифрой 1 после 6, т. е. числом 61; по сельскому хозяйству – 63, по домоводству – 64, торговле и путям сообщения – 65, промышленности и технологии – 66, и т. п. Точно так же в 9-м классе все книги по географии относятся к отделу № 91, и т. п.

Присоединение к двум первым цифрам третьей характеризует ее содержание еще ближе, указывая, к какому именно подотделу данного отдела она относится. Например, в отделе математики (51) присоединение, на третьем месте, цифры 1 указывает, что книга относится к арифметике; цифры 2 – к алгебре, и т. д. Поэтому все книги по арифметике имеют первые три цифры № 511, по алгебре – 512, геометрии – 513 и т. д. Точно так же и отдел физики (53) разбивается на 10 подотделов: книги по электричеству обозначаются № 537, по оптике – № 535 и т. д.

Затем следует дальнейшее дробление подотдела на разряды, обозначаемые четвертой цифрой номера, и т. д.

В библиотеке, устроенной по десятичной системе, нахождение нужной книги упрощается до крайности. Если, например, вы интересуетесь геометрией, вы прямо идете к шкафам, где номера начинаются с пяти, отыскиваете тот шкаф, где хранятся книги № 51… и пересматриваете в нем только те полки, где стоят книги № 513…; здесь собраны все книги по геометрии, имеющиеся в данной библиотеке. Точно так же, ища книги по кооперации, вы обратитесь к книгам № 331… не заглядывая в каталог и никого не затрудняя расспросами.

Как бы обширна ни была библиотека, никогда не может случиться недостатка в числах для нумерации книг. И наоборот, отсутствие книг по каким-либо отраслям не может препятствовать применению десятичной системы: некоторый ряд номеров останется лишь неиспользованным.

Наши любимые цифры

Вероятно, все замечали на себе и на окружающих, что среди цифр есть излюбленные, к которым мы питаем какое-то особенное пристрастие. Мы, например, очень любим «круглые числа», т. е. оканчивающиеся на 0 или 5. И это пристрастие к определенным, излюбленным числам, предпочтение их другим, заложено в человеческой натуре гораздо глубже, чем обыкновенно думают. В этом отношении сходятся вкусы не только всех европейцев и их предков, например, древних римлян, – но даже диких обитателей других частей света.

При всякой переписи населения обычно наблюдается чрезмерное обилие людей, возраст которых оканчивается на 5 или на 0; их гораздо больше, чем должно быть. Причина кроется, конечно, в том, что люди не помнят отчетливо, сколько им лет, а показывают возраст, невольно «округляя» годы. Подобное же преобладание «круглых» возрастов наблюдается и на могильных памятниках древних римлян.

Эта одинаковость числовых пристрастий идет еще дальше. Германский психолог, проф. К. Марбе, подсчитал, как часто встречается в обозначениях возраста на древнеримских могильных плитах та или иная цифра, и сравнил эти результаты с повторяемостью цифр в обозначениях возраста по данным переписи в американском штате Алабама, населенном преимущественно невежественными неграми. Получилось удивительное согласие: древние римляне и современные нам негры до малейших подробностей сходятся в числовых симпатиях и антипатиях! Конечные цифры возраста, по частоте их повторяемости, располагались в обоих случаях в одинаковой последовательности, а именно:

0, 5, 8, 2, 3, 7, 6, 4, 9 и 1.

Но и это еще не все. Чтобы выяснить числовые пристрастия современных европейцев, упомянутый ученый производил такого рода опыты: он предлагал множеству лиц определить «на глаз», сколько миллиметров заключает в себе полоска бумаги, например, в палец длиною, и записывал ответы. Подсчитав затем частоту повторения одних и тех же конечных цифр, ученый получил снова тот же самый ряд:

0, 5, 8, 2, 3, 7, 6, 4, 9 и 1.

Нельзя считать случайностью, что народы, столь отдаленные друг от друга и антропологически, и географически, – обнаруживают полную одинаковость числовых симпатий, т. е. явное пристрастие к «круглым» числам, оканчивающимся на 0 или 5, и заметную неприязнь к числам некруглым (т. е. к оканчивающимся на 1, 9, 4, 6).

Вы можете и сами убедиться в постоянстве этих пристрастий, если будете, в виде опыта, предлагать большому кругу лиц назвать любое число между 1 и 10, между 11 и 20, 21 и 30, 31 и 40, 41 и 50; окажется, что большинство ответов будет оканчиваться на 5, остальные же цифры будут попадаться тем реже, чем больше они разнятся от 5; другими словами, у вас получится такая же убывающая гамма числовых симпатий, какая приведена выше.

Заметная любовь всех людей к пятеркам и десяткам находится, без сомнения, в прямой связи с десятичным основанием нашей системы счисления, т. е. в конечном итоге – с числом пальцев на наших руках. Но все же остается неразгаданной та математическая правильность, с какой слабеет эта симпатия по мере удаления от 5 и 10.

Многие не подозревают, что пристрастие к округленным числам обходится нам довольно дорого. Товарные цены в розничной продаже всегда тяготеют к этим круглым числам: некруглое число, получающееся при исчислении продажной стоимости товара, дополняется до большего круглого числа. Округленность цены достигается здесь всегда за счет покупателя, а не продавца. Общая сумма, которую страна переплачивает торговцам за удовольствие приобретать товары по круглым ценам, накопляется весьма внушительная. Кто-то дал себе труд, задолго до последней войны, приблизительно подсчитать ее, и оказалось, что население России ежегодно переплачивало в форме разницы между круглыми и некруглыми ценами на товары не менее 30 миллионов рублей – разумеется, золотых.

Не слишком ли дорогая жертва за невинную слабость к округлениям?

Глава II Камни преткновения Пифагоровой таблицы

Трудные места таблицы умножения

 
Аще кто не твердит
таблицы и гордит,
Не может познати
числом что множати
 
 
И во всей науки
несвобод от муки,
Колико не учит
туне ся удручит
 
 
И в пользу не будет
аще ю забудет.
 

Такими чуждыми для современного слуха стихами воспевал пользу Пифагоровой таблицы составитель обширного старинного русского учебника математики^[7] Леонтий Магницкий, – учебника, по которому учились в XVIII веке наши прадеды и через врата которого гениальный Ломоносов вступил юношей в храм своей учености.

Большинство из нас уже успело позабыть о том времени, когда мы приступали к изучению таблицы умножения и постепенно одолевали ее строку за строкой. Однако, некоторые, вероятно, помнят, что не все строки этой таблицы давались одинаково. Одни усваивались очень быстро, как-то сами собой, чуть не с первого раза, – например 5 × 5 = 25, 8 × 2 = 16. Другие давались гораздо труднее: сначала как будто запоминались, но скоро снова ускользали из памяти, так что приходилось возвращаться к ним много раз, прежде чем они прочно запечатлевались. Припомните, скоро ли удалось вам затвердить, что 7 × 8 = 56? По крайней мере, для многих это было одно из труднейших мест таблицы.

Между тем для овладения арифметикой необходимо безошибочное знание всей таблицы: современный способ умножения и деления многозначных чисел основывается на твердом усвоении готовых результатов умножения однозначных чисел, т. е. на знании наизусть Пифагоровой таблицы. Справедливо, писал Магницкий, что не знающий ее «во всей науки несвобод от муки». И в наши дни, как во времена Магницкого, миллионы юных школьников под всеми широтами и долготами земного шара терпеливо заняты ее затверживанием.

Стремясь облегчить этот труд, специалисты по педагогической психологии в последнее время обратили внимание на затруднительные места таблицы умножения и подвергли их обстоятельному исследованию. Результаты получились любопытные. Оказалось, что главными камнями преткновения в таблице являются для всех одни и те же строки, а именно приведенные здесь пять:

8 × 7 = 56

9 × 7 = 63

9 × 8 = 72

7 × 6 = 42

9 × 6 = 54

Из многих сотен опрошенных взрослых и детей большинство указало именно на эти пять случаев умножения как на наиболее трудные во всей таблице. Особенно единодушно указывали на строку 8 × 7 = 56.

Далее строки Пифагоровой таблицы располагались по степени трудности в таком порядке:

8 × 6

8 × 8

7 × 6

8 × 4

7 × 4

7 × 5

7 × 3

5 × 4

8 × 5

6 × 4

Затем исследователи «камней преткновения» Пифагоровой таблицы сделали такой же тщательный опрос о том, какие из 10-ти столбцов в таблице умножения являются труднейшими для усвоения. И тут ответы получились однообразные. А именно, всего труднее оказались случаи умножения на 7, затем на 8. Третье место занимает умножение на 9, четвертое – умножение на 6. Напротив, легкими строками единодушно считаются, – как и следовало ожидать – прежде всего случаи умножения на 2; затем – на 3, на 5 и на 4.

Результаты этих психологических изысканий, произведенных среди германских школьников и учителей^[8], по всей вероятности, совпадают с выводами личного опыта большинства читателей. Все, без сомнения, согласятся, что именно случаи умножения на 7, 8 и 9 были и остаются наиболее трудными для усвоения и что труднейшие из всех – строки: 8 × 7,9 × 7, 9 × 8,7 × 6 и 9 × 6; спор может идти разве лишь о порядке этих случаев по степени их трудности. Да и будучи взрослыми, победоносно преодолев все арифметические затруднения, мы порою запинаемся именно на этих случаях умножения, когда нам приходится вычислять наспех или с усталой головой; не доверяя памяти, мы стараемся проверить результат окольным путем или спрашиваем подтверждения у других: «Семью восемь – пятьдесят шесть?»

Очевидно, затруднения эти не случайны, раз они повторяются с таким постоянством. Чем же они объясняются?

Причин несколько, и все они коренятся в тех бессознательных приемах, которыми мы обычно пользуемся при запоминании чисел. В тех случаях умножения, которые мы считаем «легкими», нам оказывает поддержку какой-нибудь вспомогательный прием (хотя обычно мы об этом и не подозреваем). Например, умножение на 2 мы бессознательно заменяем более знакомым нам действием сложения: 4 × 2 = 4 + 4. Часто запоминанию помогает созвучие: «пятью пять – двадцать пять», «шестью шесть – тридцать шесть», «шестью восемь – сорок восемь». Рифмованные строки всегда легче запоминаются, особенно в молодом возрасте; недаром в старинных грамматиках, для облегчения запоминания, составлялись стихотворные бессмыслицы даже из предлогов и наречий.

Все обстоятельства, облегчающие запоминание чисел Пифагоровой таблицы, было бы долго перечислять, тем более, что они еще не установлены бесспорно. Почему строка 9x9 = 81 затверживается легче, чем 7 × 8 или 8 × 9? Вероятно, здесь помогает характерный узор числа 81: кривая восьмерка и рядом – прямая единица. Немалую роль играют и такие признаки, как цифра 5 в конце всех чисел, полученных от умножения на это число. Иные случаи легко запоминаются благодаря их частому применению в жизни (4 × 7 – четыре недели).

Особенная трудность тех пяти случаев умножения, которые при опросе сосредоточили на себе всего больше голосов, заключается именно в том, что к ним не применимо ни одно из перечисленных условий, облегчающих запоминание. Строки

8 × 7 = 56, 9 × 7 = 63, 9 × 8 = 72, 7 × 6 = 42, 9 × 6 = 54

трудны и потому, что реже других встречаются в житейском обиходе, и потому, что не звучат созвучно, и потому, что не дают опоры глазу каким-либо характерным признаком. То, что строки эти состоят из четырех различных, но близких цифр (8, 7, 6, 5), также затрудняет запоминание. Наконец, такие сходные результаты, как 56 и 54, легко смешиваются и требуют для отчетливого различения особого напряжения. В подобных неуловимых особенностях некоторых строк таблицы умножения и коренится причина, превращающая их в неизменные камни преткновения для всякого, затверживающего эту таблицу.