
Яков Перельман
Веселые задачи. Две сотни головоломок
27. Стрельба на пароходе
Хороший стрелок стоит у одного борта парохода, а у противоположного помещена мишень. Пароход движется в направлении, показанном на рис. 26 длинной стрелкой. Стрелок прицелился совершенно точно. Попадет ли он в цель?

Рис. 26. Тир на палубе парохода.
28. Под водой
На обыкновенных весах лежат: на одной чашке – булыжник, весящий ровно 2 кг, на другой – железная гиря в 2 кг. Я осторожно опустил весы под воду.
Остались ли чашки в равновесии?
29. Как это сделано?
Вы видите здесь деревянный куб, составленный из двух кусков дерева (рис. 27). Верхняя половина куба имеет выступы, входящие в выемки нижней части. Обратите внимание на форму и расположение выступов и объясните: как ухитрился столяр соединить оба куска?
3 °Cкорость поезда
Вы сидите в вагоне железной дороги и хотели бы узнать, с какой скоростью он мчится. Можете ли вы определить скорость по стуку колес?
Решения задач 21-30
21. Различно расположенных прямоугольников в этой фигуре можно насчитать 225.
22. Если речь идет о градусах температуры, то, конечно, градус Реомюра всегда больше градуса Цельсия – именно на 1/5 долю; поэтому, если в вашей комнате по Реомюру 16 градусов, то по Цельсию – 20.
Но это вовсе не значит, что на той дощечке термометра, на которой нанесены деления (на «шкале»), длина градусов у термометра Реомюра всегда должна быть больше, чем у термометра Цельсия. Длина деления зависит от того, сколько ртути в шарике термометра, и от толщины трубки. Чем больше ртути в шарике и чем тоньше канал трубки, тем выше поднимается ртуть в трубке при нагревании и тем больше промежуток между делениями шкалы. В этом смысле «градус» может иметь самую разную длину, и вполне понятно, что в термометре Реомюра такой градус может быть и меньше градуса в термометре Цельсия.
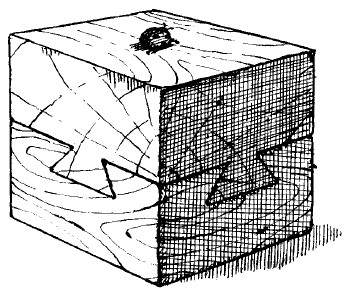
Рис. 27. Хитроумное соединение в собранном виде.
23. Легко узнать, каков был средний заработок семерых плотников. Для этого нужно избыточные 3 руб. разделить поровну между 6 плотниками и к 20 руб. каждого прибавить полученные 50 коп. Вычислили средний заработок плотника.
Отсюда узнаем, что столяр заработал
20 руб. 50 коп. + 3 руб., т. е. 23 руб. 50 коп.
24. Вот каким способом можете вы получить 100 из ряда девяти цифр и трех знаков + и —:
123 – 45 – 67 + 89 = 100
В самом деле:
123 + 89 = 212
45 + 67 = 112
212– 112 = 100
Других решений задача не имеет. Впрочем, если у вас есть терпение, попытайтесь испробовать другие сочетания.
25. Казалось бы, надо просто сложить страницы трех томов – и задача решена. Но не спешите с решением. Обратите внимание на то, как стоят книги на полке и как расположены в них страницы.
Вы видите, что 1-я страница тома I примыкает к 640-й странице тома II, а последняя страница тома III находится рядом с первой страницей тома II.
И если червь проделал ход от 1-й страницы тома I до последней страницы тома III, то он прогрыз всего только 640 страниц среднего тома да еще 4 крышки переплета, не более.
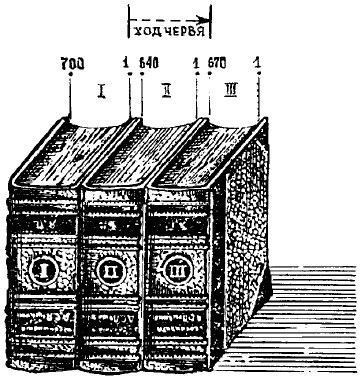
Рис. 28. Сколько страниц и крышек переплета прогрыз книжный червь?
26. Существует бесчисленное множество пар таких чисел. Вот несколько примеров:
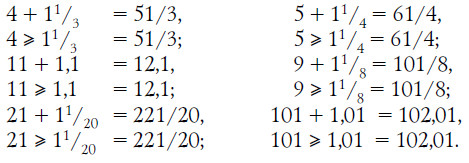
27. Конечно, меткий стрелок попадет в цель – если только пароход движется равномерно по прямой линии. Такое движение парохода ничем не может повлиять на полет пули.
Другое дело, если бы в самый момент выстрела пароход внезапно остановился, или замедлил ход, или ускорил его, или изменил курс: тогда пуля могла бы и не попасть в цель.
28. Каждое тело, если погрузить его в воду, становится легче: оно «теряет» в своем весе столько, сколько весит вытесненная им вода. Зная этот закон (открытый Архимедом), мы без труда можем ответить на вопрос задачи.
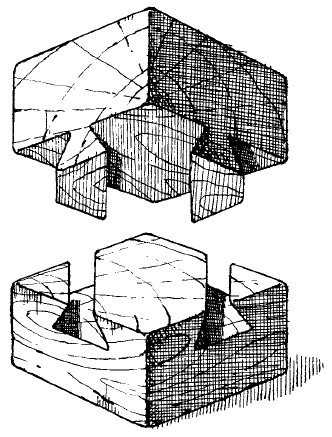
Рис. 29. Хитроумное соединение в разобранном виде.
Булыжник весом в 2 кг занимает больший объем, чем 2-килограммовая железная гиря, потому, что материал камня – гранит – легче железа. Значит, булыжник вытеснит больший объем воды, нежели гиря, и по закону Архимеда потеряет в воде больше веса, чем гиря. Следовательно, весы под водой наклонятся в сторону гири.
29. Ларчик открывается очень просто, как видно из рис. 29. Все дело в том, что выступы и углубления идут не крестом, как невольно кажется при рассматривании куба, а параллельно, в косом направлении. Такие выступы очень легко вдвинуть в соответствующие выступы сбоку.
30. Вы заметили, конечно, что при езде в вагоне все время ощущаются мерные толчки: никакие рессоры не могут сделать их неощутимыми. Происходят эти толчки от того, что колеса слегка сотрясаются в местах соединения двух рельсов, и толчок передается всему вагону. Значит, стоит лишь вам сосчитать, сколько толчков в минуту испытывает вагон, и вы будете знать, сколько рельсов пробежал поезд. Теперь остается лишь умножить это число на длину рельса, и вы получите расстояние, проходимое поездом в одну минуту.
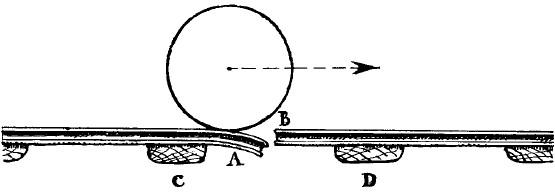
Рис. 30. Что происходит на стыке рельсов.
Обычная длина рельса – около 81/2 метра. Сосчитав с часами в руках число толчков в минуту, умножьте это число на 81/2, затем на 60 и разделите на 1000 – получится число километров, пробегаемое поездом в час:
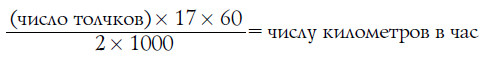
Так как
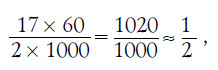
то достаточно разделить на 2 число толчков в минуту, чтобы приблизительно узнать, сколько километров пробегает поезд в час.
Обманы зрения

31. Загадочный рисунок
Пока вы смотрите на эти две физиономии (рис. 31), держа книгу неподвижно, они не обнаруживают ничего необычайного.
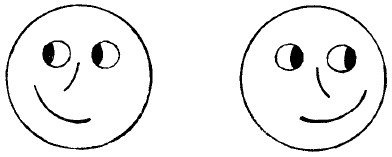
Рис. 31. Живые портреты.
Но начните двигать книгу вправо и влево, не переставая смотреть на рисунки. Произойдет любопытная вещь: физиономии словно оживут – начнут двигать зрачками вправо и влево, при этом их рот и нос также не останутся неподвижными.
Отчего это происходит?
32. Четыре фигуры
Какая из этих четырех фигур (рис. 32) самая большая и какая самая маленькая?
Дайте ответ, полагаясь только на свой глазомер.
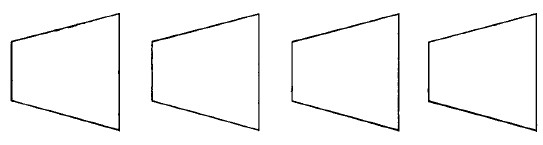
Рис. 32. Какая из четырех фигур самая большая и какая – самая маленькая?
33. Три монеты
Положите рядом три монеты – одинаковые или разные. То, что я сейчас предложу вам сделать с ними, кажется с первого взгляда очень простым. Тем неожиданнее будет для вас то, что вы узнаете потом.
Итак, выдвиньте среднюю монету вниз настолько, чтобы между нею и каждой из оставшихся двух был промежуток, равный расстоянию между А и В (рис. 33).
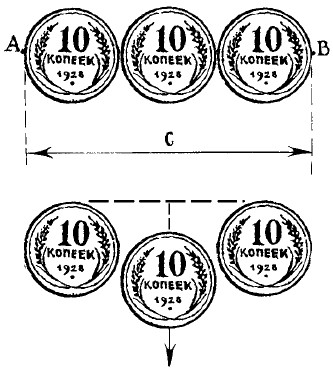
Рис. 33. Проверьте ваш глазомер: решить эту задачу с тремя монетами не так просто, как кажется.
Вы должны полагаться при этом только на свой глазомер и не прибегать к помощи линейки или циркуля. Большой точности от вас не требуется: если вы ошибетесь всего на 1 см, то задача будет считаться решенной вполне верно.
34. Кто длиннее?
Вы видите здесь три черные фигуры (рис. 34). Ответьте на вопрос: если смерить их линейкой или циркулем, какая фигура окажется длиннее?

Рис. 34. Какая фигура длиннее?
Конечно, эту задачу очень легко решить, если проделать измерения на самом деле. Но попробуйте заранее, без измерения, сказать, какая фигура длиннее, и потом проверьте себя. Вас ожидает сюрприз.
35. Кривые ноги
Почему у этих двух человек такие кривые ноги?

Рис. 35. Два великана с кривыми ногами.
36. Окружность пальца
Как вы думаете: во сколько раз окружность вашего пальца, например среднего пальца руки, меньше окружности вашего запястья?
Попробуйте ответить на этот вопрос, а потом проверьте ответ бечевкой или полоской бумаги.
Могу заранее сказать, что вы будете немало смущены результатом проверки. Почему?
37. Неожиданность
Закрыв один глаз, всматривайтесь другим в белый квадратик, нарисованный в верхней части рис. 36. Спустя десять или пятнадцать секунд вы заметите нечто совершенно неожиданное. Что именно?

Рис. 36. Черный квадрат с белым отверстием.
38. Воздушный шар
Фабричная труба на рис. 37 заслоняет часть каната, к которому привязан воздушный шар. Но художник как будто ошибся: разве канат, расположенный справа от трубы, составляет продолжение каната слева? Исправьте рисунок.

Рис. 37. Воздушный шар на привязи.
39. Какие линии?
В какую сторону изогнуты линии этого треугольника?
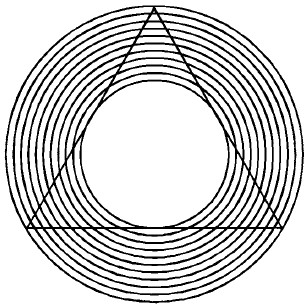
Рис. 38. У треугольника выпуклые или вогнутые стороны?
40. Дорожки сада
Что длиннее: расстояние между точками А и С или между А и В (рис. 39)?

Рис. 39. Какая из садовых дорожек длиннее?
Сначала дайте ответ, потом измерьте.
Решения задач 31-40
31. Зрачки на рисунке кажутся движущимися по той же причине, по которой оживают картины кинематографа. Когда мы смотрим на правый рисунок и затем быстро переводим взгляд на левый, то первое зрительное впечатление исчезает не сразу, а еще сохраняется на мгновение; в тот момент, когда оно исчезнет и заменится новым, нам, естественно, должно показаться, что зрачки на рисунке передвинулись от одного края глаза к другому.
32. Все четыре фигуры одинаковой величины, хотя нам и кажется, что они уменьшаются слева направо. В каждой паре правая фигура представляется меньше оттого, что левая расширяется по направлению к правой и словно охватывает ее.
33. Ваше решение, вероятно, было приблизительно таким (рис. 40).

Рис. 40. Кажущееся (неправильное) решение задачи с тремя монетами.
Оно как будто вполне верно удовлетворяет условию задачи, не правда ли? Но попробуйте измерить расстояние циркулем – окажется, что вы ошиблись чуть ли не в полтора раза!
А вот правильное расположение монет, хотя на глаз оно кажется совсем неправильным (рис. 41).
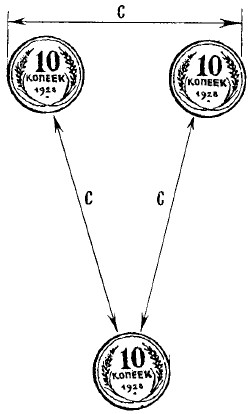
Рис. 41. Правильное решение задачи с тремя монетами.
Чем крупнее кружки, тем обман зрения поразительнее. Опыт хорошо удается и в том случае, если взять неодинаковые кружки.
34. Это интересный обман зрения: фигура человека, идущего впереди, имеет совершенно такую же длину, как и фигура последнего из идущих. Передний человек кажется нам великаном по сравнению с задним только потому, что изображен вдалеке.
Мы привыкли к тому, что предметы с удалением уменьшаются; поэтому, видя вдали неуменыненную человеческую фигуру, мы невольно заключаем (раз она кажется крупной даже на большом расстоянии), что это – человек исполинских размеров.
35. У этих людей ноги вовсе не кривые! Вы можете проверить их прямизну по линейке – все 8 линий идут совершенно прямо и параллельны между собой.
Проверку можно выполнить и без линейки: держите книгу на уровне глаз и смотрите вдоль линий ног, и вы ясно увидите, что ноги прямые.
Кажущаяся кривизна представляет собой любопытный обман зрения, который особенно усиливается, если смотреть на рисунок сбоку.
36. Результат проверки смутит вас потому, что обнаружит грубую ошибочность ответа. Вы, наверное, думали, что окружность пальца раз в 5–6 меньше окружности запястья. Между тем нетрудно убедиться, что окружность запястья всего лишь… в три раза больше пальца!
Отчего происходит такой обман зрения – трудно объяснить.
37. Неожиданное явление состоит в том, что через 10–15 сек нижняя белая полоса совершенно пропадает – на ее месте будет сплошной черный фон!
Спустя 1–2 сек полоса снова появится, затем вновь исчезнет, чтобы появиться опять, и т. д.
Это загадочное явление объясняется, вероятно, утомляемостью нашего глаза.
38. Рисунок сделан совершенно правильно. Приложите линейку к канату, и вы убедитесь, что вопреки очевидности его части составляют продолжение одна другой.
39. Линии нисколько не изогнуты ни внутрь, ни наружу, а кажутся вогнутыми внутрь оттого, что их пересекают насквозь несколько дуг.
40. Как ни странно, АС = АВ.
Десять затруднительных положений

41. Жестокий закон
Жил некогда жестокий правитель, который не желал никого впускать в свои владения. У моста через пограничную реку был поставлен часовой, вооруженный с головы до ног, и ему было приказано спрашивать каждого путника:
– Зачем идешь?
Если путник говорил неправду, часовой обязан был схватить его и тут же повесить. Если же путник отвечал правду, ему и тогда не было спасения: часовой должен был немедленно утопить его в реке.
Таков был суровый закон жестокосердного правителя, и неудивительно, что никто не решался приблизиться к его владениям.
Но вот нашелся крестьянин, который, несмотря на это, спокойно подошел к охраняемому мосту у запретной границы.
– Зачем идешь? – сурово остановил его часовой, готовясь казнить смельчака, безрассудно идущего на верную гибель.
Но ответ был таков, что озадаченный часовой, строго исполняя жестокий закон, не мог ничего поделать с догадливым крестьянином.
Каков же был ответ?
42. Милостивый закон
В некотором государстве был такой обычай. Каждый преступник, осужденный на смерть, тянул перед казнью жребий, который давал ему надежду на спасение. В ящик опускали две бумажки: одну со словом «жизнь», другую со словом «смерть». Если осужденный вынимал первую бумажку, он получал помилование, если же имел несчастье вынуть бумажку со словом «смерть», приговор приводился в исполнение.
У одного человека, живущего в этой стране, были враги, которые оклеветали его и добились, чтобы суд приговорил несчастного к смертной казни. Мало того, враги не желали оставить невинно осужденному ни малейшей возможности спастись. В ночь перед казнью они вытащили из ящика бумажку со словом «жизнь» и заменили ее бумажкой со словом «смерть». Значит, какую бы бумажку ни вытянул осужденный, он не мог избегнуть смерти.
Так думали его враги. Но у него были друзья, которым стали известны козни врагов. Они успели предупредить осужденного, что в ящике оба жребия имеют надпись «смерть». Друзья убеждали несчастного открыть перед судьями преступный подлог его врагов и настаивать на осмотре ящика с жребиями.
Но, к их изумлению, осужденный просил друзей хранить проделку врагов в строжайшей тайне и уверял, что тогда он будет наверняка спасен. Друзья приняли его за сумасшедшего…
Наутро осужденный, ничего не сказав судьям о заговоре своих врагов, тянул жребий и – был отпущен на свободу! Как же ему удалось так благополучно выйти из, казалось бы, безнадежного положения?
43. Учитель и ученик
То, что описано ниже, произошло, говорят, в Древней Греции. Учитель мудрости, софист Протагор, взялся обучить Квантла всем приемам адвокатского искусства. Между учителем и учеником было заключено условие, по которому ученик обязывался уплатить своему учителю вознаграждение тотчас же после того, как впервые обнаружатся его успехи, т. е. после первой же выигранной им тяжбы.
Квантл прошел уже полный курс обучения. Протагор ожидает платы, но ученик не торопится выступать на суде защитником. Как же быть? Протагор, наконец, решил взыскать с ученика долг по суду и подал на ученика в суд. Он рассуждал так: если дело будет им выиграно, то деньги должны быть взысканы на основании судебного приговора; если же тяжба будет им проиграна и, следовательно, выиграна его учеником, то деньги опять-таки должны быть уплачены Квантлом по уговору – платить после первой же выигранной учеником тяжбы.
Однако ученик, напротив, считал тяжбу Протагора совершенно безнадежной. Он, как видно, действительно кое-что перенял у своего учителя и рассуждал так: если его присудят к уплате, то он не должен платить по уговору – ведь он проиграл первую тяжбу; если же дело будет решено в его пользу, то он опять-таки не обязан платить – на основании судебного приговора.
Настал день суда. Судья был в большом затруднении. Однако после долгого размышления он нашел, наконец, выход – такой приговор, который, нисколько не нарушая условий соглашения между учителем и учеником, в то же время давал учителю возможность получить обусловленное вознаграждение.
Каков был приговор судьи?
44. На болоте
Отряд французских солдат во время похода в Алжире очутился однажды в местности, совершенно лишенной растительности и притом с почвой настолько болотистой, что, хотя по ней и можно было ступать, сесть на нее было совершенно невозможно. Усталый отряд продвигался вперед в поисках подходящего места для привала, но на десятки верст простиралась все та же болотистая почва. Как отдохнуть, если нет кругом ни единого сухого местечка и ничего такого, что можно было бы подложить или на что можно было бы сесть?
И все-таки одному солдату пришла в голову счастливая мысль, которая помогла отряду выйти из затруднительного положения. Солдаты уселись и отдохнули.
Как? Отгадайте!
45. Три разведчика
В не менее затруднительном положении оказались однажды трое пеших разведчиков, которым необходимо было перебраться на противоположный берег реки при отсутствии моста. Правда, на реке катались в челноке два мальчика, готовые помочь солдатам. Но челнок был так мал, что мог выдержать вес только одного солдата. Даже солдат и один мальчик не могли одновременно сесть в лодку без риска ее потопить. Плавать же солдаты совсем не умели.
Казалось бы, при таких условиях мог переправиться через реку только один солдат. Однако все три разведчика вскоре благополучно очутились на противоположном берегу и возвратили лодку мальчикам. Как они это сделали?
46. Слишком много предков
У меня есть отец и мать. У моего отца и у моей матери тоже, конечно, были отец и мать. Значит, восходя к 3-му поколению, я нахожу у себя 4 предков.
Каждый из моих двух дедов и каждая из моих двух бабушек также имели отца и мать. Следовательно, в 4-м поколении у меня 8 прямых предков. Восходя к 5-му, 6-му, 7-му и т. д. поколениям я нахожу, что число моих предков все возрастает и притом чрезвычайно заметно, именно:
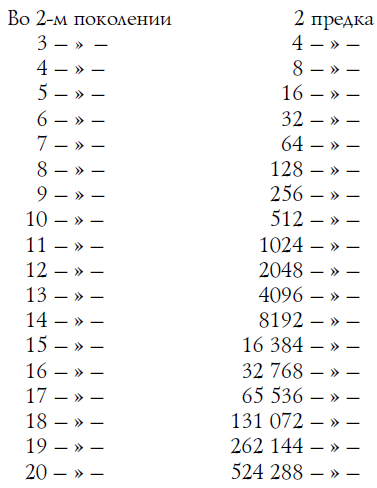
Вы видите, что 20 поколений назад у меня была уже целая армия прямых предков, больше полумиллиона. И с каждым предыдущим поколением это число удваивается.
Если считать, как обыкновенно принимается, по три поколения в столетие, то в начале нашей эры, 19 веков тому назад, на Земле должно было жить несметное количество моих предков: можно вычислить, что число их записывается 18 цифрами.
Чем дальше в глубь веков, тем число моих предков должно возрастать. В эпоху первых фараонов численность их должна была доходить до умопомрачительной величины. В каменный век, предшествовавший египетской истории, моим предкам было уже, вероятно, тесно на земном шаре.
Но ведь и у вас, читатель, было столько же прямых предков. Прибавьте их к моим и присоедините еще предков всех своих знакомых, да прибавьте еще предков всех вообще людей, живущих ныне на Земле, и вы легко вообразите, в какой страшной тесноте жили наши предки: ведь для них буквально не хватало места на земном шаре!
Не укажете ли вы им выход из этого затруднительного положения?
47. В ожидании трамвая
Три брата, возвращаясь из театра домой, подошли к рельсам трамвая, чтобы вскочить в первый же вагон, который подойдет. Вагон не показывался, и старший брат предложил подождать.
– Чем стоять здесь и ждать, – ответил средний брат, – лучше пойдем вперед. Когда вагон догонит нас, тогда и вскочим; а тем временем часть пути будет уже за нами – скорее домой приедем.
– Если уж идти, – возразил младший брат, – то не вперед по движению, а в обратную сторону: тогда нам, конечно, скорее попадется встречный вагон, мы раньше и домой прибудем.
Так как братья не могли убедить друг друга, то каждый поступил по-своему: старший остался ожидать на месте, средний пошел вперед, младший – назад.
Кто из трех братьев раньше приехал домой? Кто из них поступил благоразумнее?
48. Куда девался гость?
Можно ли посадить 11 гостей на 10 стульев так, чтобы на каждом стуле сидело по одному человеку? Вы думаете – нельзя? Нет, можно – надо только умеючи взяться за дело.
Поступите так. Первого гостя посадите на первый стул. Затем попросите 11-го гостя сесть временно на тот же первый стул. Усадив этих двух гостей на первый стул, вы усаживаете:
3-го гостя на 2-й стул
4-го —»-»– 3-й —»—
5-го —»-»– 4-й —»—
6-го —»-»– 5-й —»—
7-го —»-»– 6-й —»—
8-го —»-»– 7-й —»—
9-го —»-»– 8-й —»—
10-го —»-»– 9-й —»—
Как видите, остается свободным 10-й стул На него вы и посадите 11-го гостя, который временно сидел на 1-м стуле. Теперь вы счастливо вышли из затруднительного положения: у вас рассажены все 11 гостей на 10 стульях.
А все-таки, куда девался один гость?
49. Без гирь
Вам принесли на дом 10 кг сливочного масла. Вы желаете купить всего только 5 кг. У одного соседа нашлись весы с коромыслом, но гирь нет ни у вас, ни у разносчика и ни у одного из соседей. Можете ли вы без всяких гирь отвесить 5 кг от 10?
50. На неверных весах
Представьте себе, что когда вы догадались, наконец, как отвесить масло без гирь, входит ваш сосед, ссудивший вам весы, и сообщает, что весы его очень ненадежны – на верность их полагаться нельзя.

Рис. 42. Взвешивание без гирь.
Можете ли вы даже и на неверных весах, притом без гирь, отвесить правильно 5 кг от 10-килограммового куска?







