Валентин Юльевич Арьков
Корреляционный и регрессионный анализ в электронных таблицах. Лабораторный практикум

© Валентин Юльевич Арьков, 2020

ISBN 978-5-0050-4576-8

Создано в интеллектуальной издательской системе Ridero

Предисловие

Данная лабораторная работа позволяет освоить базовые методы исследования взаимосвязей в электронной таблице – корреляционный и регрессионный анализ.

При выполнении лабораторной работы используются знания и навыки, полученные на предыдущих занятиях.

Условные обозначения:

– жирный шрифт – названия функций и пунктов меню;

– КНОПКИ на экране компьютера;

– КЛАВИШИ на клавиатуре компьютера.

Описывается работа в англоязычной версии Microsoft Excel из пакета Office 365. В тексте приводятся названия пунктов меню и функций на английском и на русском языках. На рисунках используется английская версия пакета.

Введение

В данной лабораторной работе рассматривается корреляционная зависимость, или корреляция [1—4].

В работе для изучения взаимосвязи используются методы корреляционного и регрессионного анализа, а также сводка и группировка данных. Работа выполняется в пакете Excel [5].

Корреляционный анализ позволяет оценить степень тесноты связи. Регрессионный анализ используется для построения линейных и нелинейных моделей.

На первом этапе исходные данные получают путём имитационного моделирования. На втором этапе проводится анализ реальных данных.

Требования к оформлению отчёта приведены в описании предыдущей лабораторной работы [6].

Общие сведения

Корреляция – это связь между двумя случайными величинами, которые часто называют следующим образом:

X – факторный признак;

Y – результативный признак.

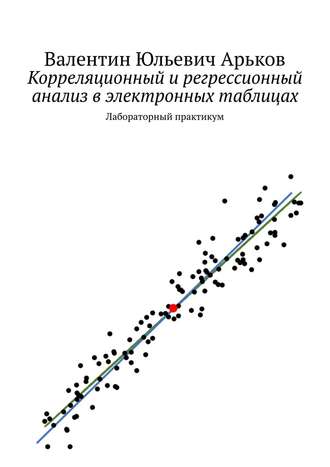
Изображение исходных данных называется диаграммой разброса. Каждая пара чисел X и Y изображается отдельной точкой. Точки между собой не соединяют.

Пример диаграммы разброса для корреляционной зависимости показан на рисунке ниже.

Корреляция

Варианты задания

Варианты заданий представлены в таблицах.

В каждом варианте рассматриваются два набора данных – примеры линейной и нелинейной регрессии. Анализ проводится для обоих случаев.

Факторный признак Х – случайная величина с равномерным распределением.

Случайная составляющая Е – случайная величина со стандартным нормальным распределением (нулевое среднее и единичная дисперсия).

Результативный признак Y вычисляется по формуле.

Объём выборки n = 200.

На новом листе опишите вариант задания.