Сергей Фёдорович Гаврилов
Расчеты в Excel

Вес усеченного конуса

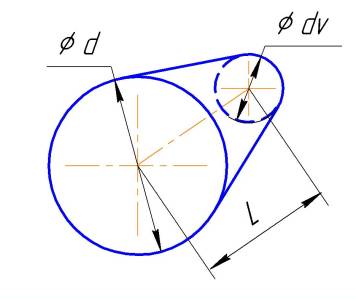
Брус в виде усеченного конуса.

Больший диаметр d = 600.

Меньший диаметр dv = 200.

Длина бруса L = 300.

Рис. Конус усеченный.

Объем усеченного конуса:

V=(L * Pii / 3)*( Rb*Rb + Rm * Rm + Rb * Rm )..;

V=(300 * Pii / 3)*( 90000 + 10000 + 30000 )..;

V = 40840704,5…

Масса бруса:

Q= 7,85 * V / 1000000..; Q= 7,85 * 40840704,5 / 1000000..;

Q = 320,59953 кг..

Другой вариант расчета @012. :

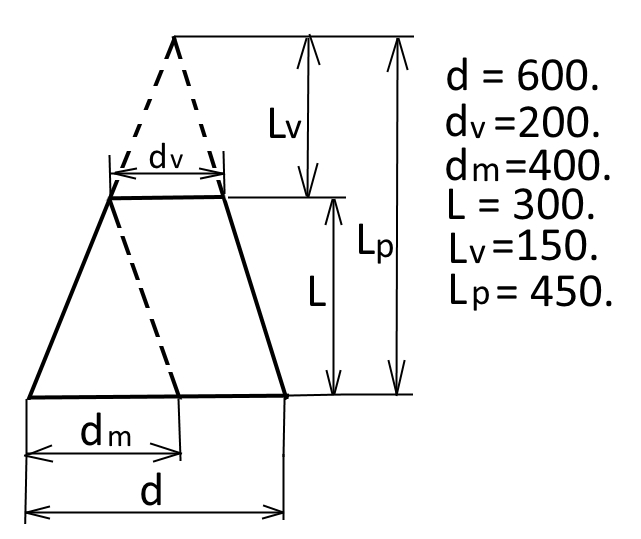
Рис. Конус усеченный Вариант 2.

,,,

,,,

Штриховая линия, параллельная правой образующей отсекает три подобных треугольника.

Треугольник с основанием «dm» и высотой «L» и треугольник с основанием «d» и высотой «Lp».

Основание dm=d-dv.. dm=600-200.. dm=400.. Решая пропорции находим высоту Lp..

Lp=d*L/dm.. Lp=600*300/400.. Lp=450.. Lv=Lp-L.. Lv=450-300.. Lv=150..

Объем конуса равен произведению площади основания на одну треть высоты.

Находим объемы конусов с основаниями «d» и «dv»: V = Pii*d*d*Lp*(1/3)/4..

V = Pii*600*600*450*(1/3)/4.. V = 424115001.. Аналогично Vv=1570796..

Объем усеченного конуса это разность объемов Vу = 424115001-1570796..

Vу =40840705.. Вес усеченного конуса Q = 320,599 кгс.

Запись программы в Excel

Первым делом откроем лист Excel по имени Е_04. ( Скачать из приложения ).

Сохраним его как Е 06. Далее на листе необходимо выполнить заголовок расчета «Вес усеченного конуса».

Просто меняем надпись в заголовке.

@002А. Ставим курсор в ячейку А17 Нажимаем левую кнопку мыши и с нажатой кнопкой ведем вверх

до ячейки А2. Столбик А2-А17 выделяется. Ставим курсор в выделенный столбик и жмем

правую кнопку мыши.

Появится табличка Рис 03. В ней выбираем пункт «Формат ячеек». После щелчка на «Формате ячеек»появится табличка Рис 04: В этой табличке выберем в колонке «Число»– выбираем «Общее»

размер шрифта надписей ( 16 ), цвет шрифта ( черный ), можно выполнить границу выделенной области в виде рамки ( делаем без границы ). Можно залить ( окрасить ) выбранную область.

@003. – В пункте «Защита»– выберем «защищаемая ячейка». В этом режиме, при работе с таблицей,

надпись в этой ячейке изменить не получится – надпись остается неизменной.

Точно также обработаем столбик «С». С2-С17. В этом столбике будет выведены названия результатов расчета.

Форматируем так же как А2…Ф17.

Затем меняем надписи в столбике исходных данных:

В ячейке А5 Надпись «Высота», в ячейке А7 пишем «Диаметр основания»,

в ячейке А9 пишем «Диаметр вершины»,

в ячейке А11 пишем «Удельный вес в т/куб.м.»,

Выделяем ячейки С2…С17 – это будут ячейки с названиями выводимых результатов расчета.

Аналогично как в столбике А2…А17 пишем в ячейках названия результатов расчета

@004А. Выделяем ячейки В2…В17. В этом столбике будем вводить исходные данные для расчета.

Ставим курсор в выделенный столбик и жмем правую кнопку мыши.

Появится табличка Рис 03. В ней выбираем пункт «Формат ячеек». После щелчка на «Формате ячеек»появится табличка Рис 04: В этой табличке выберем размер шрифта надписей ( 16 ), цвет шрифта ( черный ),

В графе «Число»выбираем формат «Числовой». В графе «Выравнивание» выбираем выравнивание

как по вертикали, так и по горизонтали по центру. В графе «Защита»нужно убрать защиту ячеек. Ентер.

@005. Ячейки вывода результата D2…. D17, ставим галочку «Скрыть формулы». Защиту уберем.

Заливку сделаем светло желтой. В графе «Число» выбираем формат «Числовой».

Выравнивание все по центру. Размер шрифта 16.

Выделяем ячейки Е2…Е17. Столбик форматируем точно как ячейки D2…. D17.

Проверяем чтобы в ячейке D2..D17.; Е2, Е17 – Была снята защита, но стояла галочка «Скрыть формулы».

Объем конуса равен одной трети произведения площади основания на высоту.

Находим высоту полного ( не усеченного ) конуса: Е4=((B9/2)*B5)/B7..

Находим площадь основания: D9=B9*B9*ПИ()/4.. Объем = Е12=D9*E4/3..

Находим высоту срезанной верхушки конуса: hm=Е4-B5..

Находим площадь основания срезанной верхушки : D10=B7*B7*ПИ()/4.. Объем = Е13=D10*(E4-В5)/3..

Объем усеченного конеса: D4=Е12-Е13..

Находим образующую полного конуса как гипотенузу: Е5=(В9/2)*(В9*2)+(Е4*Е4)..

Образующая Е6=КОРЕНЬ(Е5).. Это большой радиус развертки. Малый радиус развертки найдем по соотношению Радиусов оснований и высот конусов. Далее находим площадь кольца с радиусами большим и малым развертки. Далее находим полный угол развертки как соотношение длинн окружностей с радиусом основания полного конуса к окружности с большим радиусом развертки. По этому соотношению находим боковую площадь конуса как часть площади кольца. При затруднениях – смотри расчетный открытый лист

в приложении по ссылке на яндекс диске. Вы заметили, что используется столбик Е2…Е13 – для вычисления промежуточных величин и столбик F2…F13 для пояснения – что это за величины. В рабочем листе

столбик F2…F13 был удаелен, а столбик Е2…Е13 был сделан узким для сокрытия цифр.

Примечание: Если в результате вычисления в ячейке появляется вместо результата ##### – то скорей всего столбик слишком узкий – надо его расширить – смотри @004.

Забив все формулы – Проверяем правильность записей – расчетом с контрольными цифрами.

Если все правильно – сохраняем лист как Е 06. Затем сохраняем как Е 06_Z.

Включаем защиту листа Е 06_Z. Смотри @007.

Вес сегмента круга

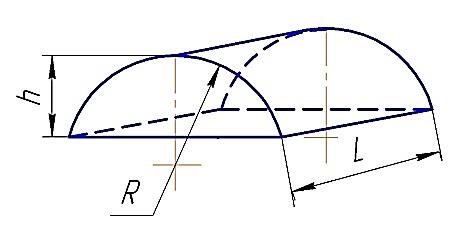
Радиус сегмента R = 300.

Высота сегмента h = 200.

Длина бруса L = 400.

Материал – сталь q = 7,85 т / куб.м.

Рис. Брус Сегмент круга.

Расчет:

Диаметр круга:

.d=R+R ; d= 300 + 300; d= 600…

Площадь круга:

Sk= d * d * Pii / 4..; Sk= 600 * 600 * Pii / 4..; Sk= 282743,3388…

Высота треугольника под сегментом:

.a=R-h..; a= 300 – 200; a= 100…

Половина основания треугольника:

.b= sqrt((R*R)-(a*a))..; b= sqrt((300*300)-(100*100))..; b= 282,8427125…

Площадь треугольника:

St= a * b..; St= 100 * 282,8427125..; St= 28284,27125…

Угол из центра круга на концы сегмента:

U = arctan( b / a )..; U = arctan( 282,8427125 / 100 );

U = 70,52877937…

Площадь кругового сектора

Ss=Sk * U * 2 / 360..; Ss= 282743,3388 * 70,52877937 * 2 / 360..;

Ss= 110786,3476…

Площадь сегмента круга

Sg=( Ss – St )..; Sg=( 55393,17378 – 28284,27125 )..; Sg= 82502,07631…

Q = 7,85 * Sg * L / 1000000..; Q = 7,85 * 82502,07631 * 400 / 1000000..;

Q = 259,05652 кг..

Запись программы в Excel

Первым делом откроем лист Excel по имени Е_06. ( Скачать из приложения ).

Сохраним его как Е 07. Далее на листе необходимо выполнить заголовок расчета «Вес сегмента круга».

Просто меняем надпись в заголовке. Далее просто меняем надписи в исходных данных и надписи в результатах расчета. Далее ведем сам расчет: Сначала найдем площадь круга от которого отрезали сегмент.

Площадь круга:

Sk= d * d * Pii / 4; Sk= (R+R) * ( R+R) * Pii / 4; Sk= 600 * 600 * Pii / 4; Sk= 282743,3388…

В Excel. D9 =(B7+B7)*(B7+B7)*ПИ()/4..

Высота треугольника под сегментом: .a=R-h; .a= 300 – 200; .a= 100… В Excel E14=B7-B5..

Половина основания треугольника:

.b= sqrt((R*R)-(a*a)); b= sqrt((300*300)-(100*100)); b= 282,8427125…

В Excel E15=((B7*B7)-(E14*E14))… E16=КОРЕНЬ(E15)…

Площадь треугольника: St= a * b;.. St= 100 * 282,8427125;.. St= 28284,27125…

В Excel D11=E16*E14..

Угол из центра круга на концы сегмента: Угол находится в радианах. Смотри @008А.

U = arctan( b / a );.. U = arctan( 282,8427125 / 100 );.. В Excel E17=E16/E14.. D6=ATAN(E17)..

Находим какую часть круга занимает сектор ( 2*Пи = 360 градусов – это полный круг ).

E18=D6/ПИ()..

Площадь сектора круга: D1=D9*E18..

Площадь сегмента ( из площади сектора долой площадь треугольника): D4=D10-D11..

Вес сегмента: =D4*B9*B11/1000000… Q = 259,05652 кг…

В закрытом ( рабочем ) листе столбик Е2…Е18 был сделан узким для сокрытия цифр.

А шрифт столбика F – сделали очень бледного цвета – чтоб не отвлекал внимания.

Примечание: Если в результате вычисления в ячейке появляется вместо результата #### – то скорей всего столбик слишком узкий – надо его расширить – смотри @004.

Забив все формулы – Проверяем правильность записей – расчетом с контрольными цифрами.

Если все правильно – сохраняем лист как Е 07. Затем сохраняем как Е 07_Z.

Включаем защиту листа Е 07_Z. Смотри @007.

Вес кольца

Вес кольца с профилем в сечении в виде трапеции.

Рис. Кольцо выпуклое.

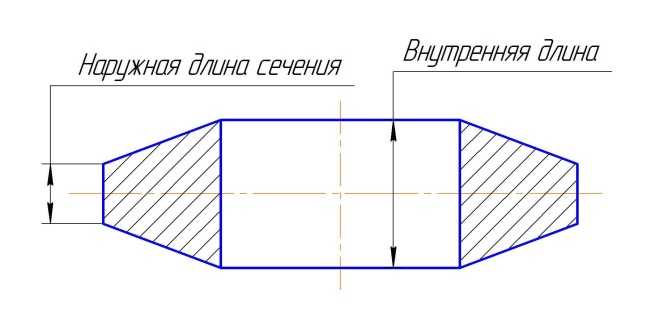
Расчет ведется так: Деталь разбивается на три элемента.

1 – Диск с наружным диаметром – равным диаметру кольца толщиной наружной длиной сечения.

2 – Два усеченных конуса с диаметром основания равным диаметру кольца.

С диаметром вершины равным диаметру отверстия.

С высотой усеченного конуса равным Н = ( Внутренняя длина – Наружная длина ) / 2 ..

3 – Отверстие считается как диск толщиной равной внутренней длине.

Вес считаем: Вес = ( Вес диска + Вес усеченного конуса *2 ) – Вес диска отверстия.

Алгоритмы расчета веса элементов приведены ранее.

Кольцо с профилем широким на наружном диаметре.

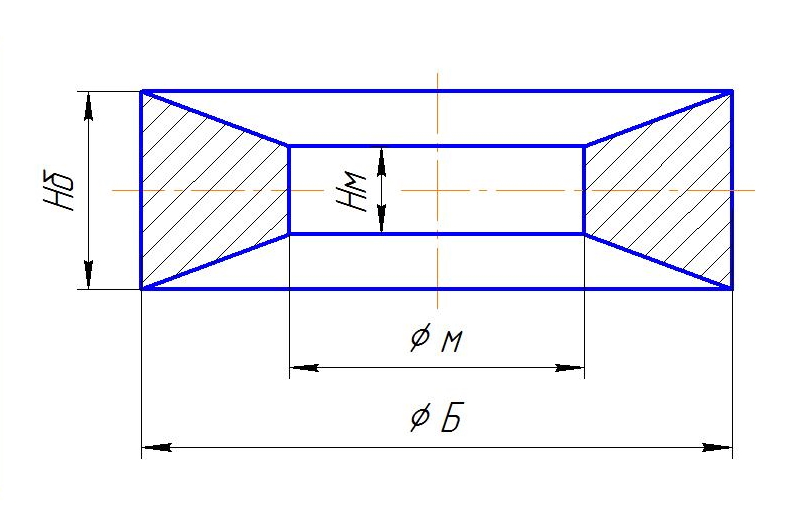
Рис. Кольцо вогнутое.

Деталь так же разбивается на три элемента.

1 – Диск с наружным диаметром – равным диаметру кольца Ф Б и длиной Нб.

2 – Два усеченных конуса с диаметром основания равным диаметру кольца Ф Б.

С диаметром вершины равным диаметру отверстия Ф м.

С высотой усеченного конуса равным Н = ( Нб – Нм ) / 2 ..

3 – Отверстие считается как диск Ф м толщиной равной внутренней длине Нм.

Вес считаем: Вес = Вес диска Ф Б – ( Вес усеченного конуса *2 + Вес диска отверстия ).

Примечание: Часто приходится считать вес шкива клиноременной передачи.

Рассчитывают вес диска шкива не принимая во внимание канавки под ремни.

Рассчитывают вес вырезанного металла под одну канавку – как вес кольца.

Далее из веса диска шкива удаляют веса колец с профилем канавки клинового ремня.

…..

Расчеты веса элементов деталей быстрей выполнять используя программу. Программу можно скопировать из книги «Python 3 Расчет веса детали .». Программа значительно экономит время и уменьшают вероятность ошибок в расчете.. Программы можно выполнить так же в Excel.

Запись программы в Excel

Первым делом откроем лист Excel по имени Е_06. ( Скачать из приложения ).

Сохраним его как Е_08. Далее на листе необходимо выполнить заголовок расчета:

«Вес кольца в сечении трапеция».

Просто меняем надпись в заголовке. Далее просто меняем надписи в исходных данных и надписи в результатах расчета. Для облегчения программирования используем фрагменты уже разработанной программы по расчету веса о объема усеченного конуса, и по объему цилиндра. Далее ведем сам расчет: Расчитаем усеченный конус.

Расчитаем по другому варианту расчета @012.: Высота усеченного конуса Е6=(B11-B9)/2..

Высота полного конуса Е4=B5*E6/(B5-B7).. Высота срезанной верхушки конуса Е5=E4-E6..

Площадь основания: D9=B5*B5*ПИ()/4.. Площадь основания верхушки: D10=B7*B7*ПИ()/4..

Объем полного конуса: Е9=D9*E4/3.. Объем отсеченной верхушки: Е8=D10*E5/3..

Объем усеченного конуса как разность объемов полного конуса и срезанной верхушки:

Е11=E9-E8.. Расчеты объемов дисков смотри в разделе Вес круглого бруса.

Объем диска с наружным диаметром: Е13 =B9*B5*B5*ПИ()/4..

Объем диска с внутренним диаметром: Е14=B11*B7*B7*ПИ()/4..

Объем кольца считаем: (Объем диска наруж. диам.+ двойной объем усеченного конуса ) минус объем диска отверстия. D4=(E13-E14)+E11+E11.. Далее объем умножаем на удельный вес материала.

@013.: Для наглядности выделим область ячеек G2-G9..K2-K9.. Щелкаем на значке объединения ячеек-

Смотри Рис. 02. Далее вставляем рисунок в эту область так же как вставляем рисунок в Word. Открыв в главном меню – подменю «Вставка» и далее иконку «Рисунок».

,,,,

Расчет кольца с широким наружным и узким внутренним краем производится аналогично..

Примечание:

Для пересчета веса бруса из стали на вес бруса из другого материала –

умножаем вес стального бруса на коэффициент из таблицы В-01.

К примеру алюминий легче стали. По расчету имеем массу стального бруса = 100 кг.

Если этот брус будет из алюминия, то его масса Ма = Мс*k.. Ма = 100*0,35032.. = 35,032 кг..

Рис. Таб. Перевод плотности.

Вот выполнен первый блок расчетов «Вес». Для того, чтобы этими расчетами было удобно пользоваться – сделаем лист оглавления с именем «Оглавление Вес бруса».

@019. Лист «Оглавления»должен находиться в той же папке, что и листы расчета веса.

Желательно, чтобы расчетные листы все были закрытыми.

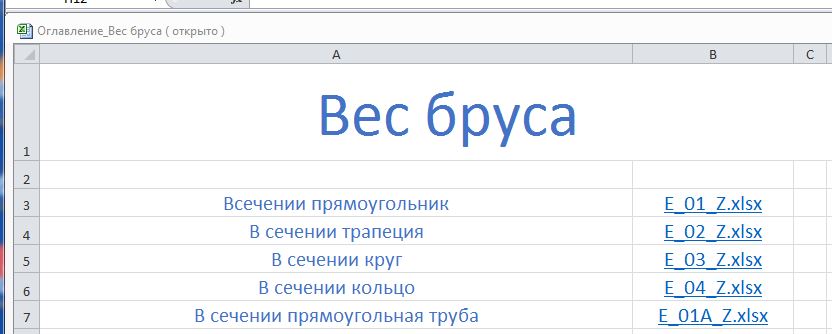
Лист «Оглавления» имеет две рабочие колонки ( смотри в ссылке ) и на рисунке.

Рис. Экран Excel Оглавление.

,,,

,,,

В колонку «А» вписываем названия расчетов, в колонку «В» адреса ссылок на листы, где эти расчеты производятся. Для этого на листе откроем раздел «Вставка» смотри синюю стрелку.

Рис. Экран Excel Гипер ссылка.

,,,.

,,,

Выбираем ячейку в колонке «В» щелкаем ( стрелка № 1 ).

В разделе «Вставка» щелкаем на «Гипер ссылку» смотри красную стрелку.

Появляется добавочное меню.

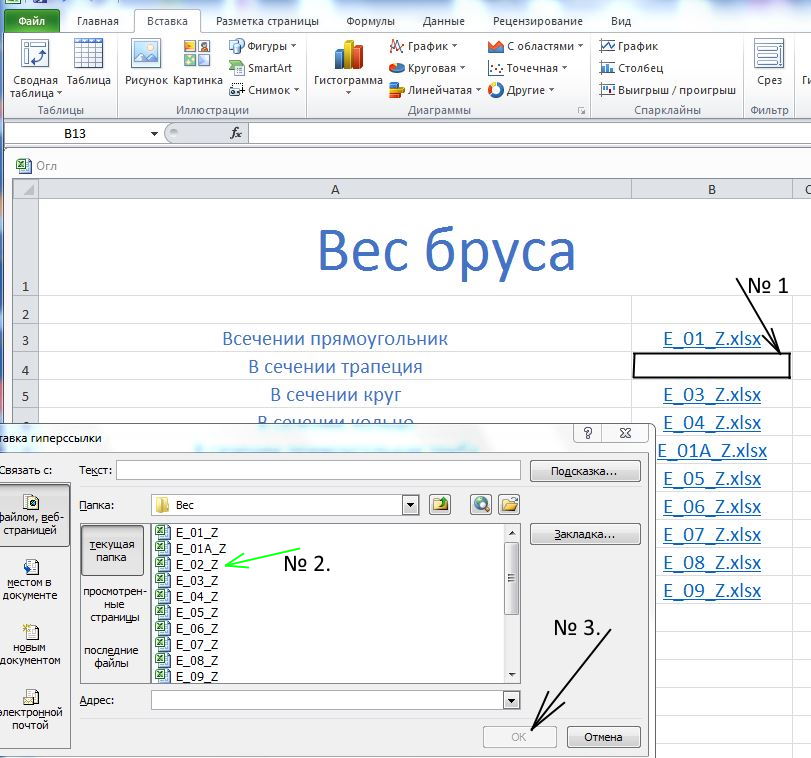
Рис. Экран Excel вставка гиперссылки.

,,,,

,,,,

В добавочном меню щелкаем на название необходимого листа расчетов – смотри зеленую сторелку № 2, затем на клавишу «ОК»– стрелка № 3. Таким образом – напротив наименования расчета в столбик «В»вставляем ссылки на расчетные листы.

Вставив все ссылки на расчетные листы – колонки» «А» и «В»выделим @002.

Откроем «Формат ячеек»– «Защита»– @003. Выберем защищенные ячейки.

При блокировании листа паролем @007.

Должна быть галочка в строке «выбирать защищенные ячейки» см. рис 5..

Расчеты геометрии

Отрезок на плоскости

Исходные данные:

Даны координаты концов отрезка:

Абсцисса x1 = 10; Ордината y1 = 20;

Абсцисса x2 = 50; Ордината y2 = 80;

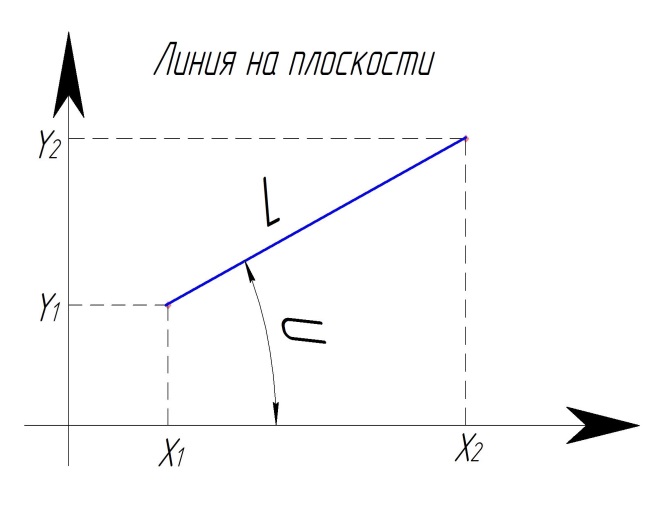
Рис. Линия на плоскости.

,,,

Расчет:

Длина отрезка:

L= sqrt((x1-x2)*(x1-x2))+((y1-y2)*(y1-y2));

L= sqrt((10-50)*(10-50))+((20-80)*(20-80));

L= sqrt( 5200 ); L= 72,11102551…

Угол между осью Х-Х и отрезком:

U= arctan((y2-y1)/(x2-x1));

U= arctan( 60 / 40 ); U= 56,30993247…

……..

Запись программы в Exрcel

Первым делом откроем лист Excel по имени Е_00. ( Скачать из приложения ).

Сохраним его как Е 10. Далее на листе необходимо выполнить заголовок расчета:

«Линия на плоскости». Далее форматируем столбики как описано @002. @003. @004. @004А.

Выполняем защиту столбиков и сохраняем лист как Е 10. Затем сохраняем как Е 10_Z.

Проверим форматирование столбиков и защитим лист @007.

Примечание: Если Запись программы в Exрcel. такая краткая – значит ничего нового в программировании

этой программы ( листа ) нет. Если нужны подробности – скачайте по ссылке приложение. В приложении

есть открытые и закрытые листы. Открытые листы для рассмотрения подробностей. Закрытые листы –

для практических расчетов.

Расчет линейной интерполяции

Линейная интерполяция применяется при работе с табличными данными.

Из таблицы имеем две взаимосвязанных пары значений какой то функции.

Необходимо вычислить ординату при значении абсциссы близком взятой из таблицы пары абсцисс.

Например: Абсцисса x1 = 10; Ордината y1 = 20;

Абсцисса x2 = 90; Ордината y2 = 180;

Необходимо вычислить Ординату Yx при Абсциссе Хх = 50;

Примечание: Абсцисса Хх может также быть немного больше

или меньше крайних значений известных табличных Абсцисс.

Рис. Линейная интерполяция.

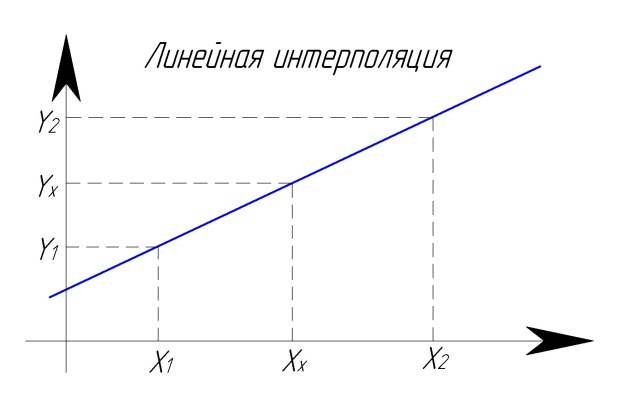
Расчет: RF-01.

Yy = (((y2-y1)*(Хx-x1)) / (x2-x1))+y1; Yy = (((180-20)*(50-10)) / (90-10))+20;..

Yy = ( 6400 / 80 )+20; Yy = 100;..

,,,,

Запись программы в Excel

Первым делом откроем лист Excel по имени Е_10. ( Скачать из приложения ).

Сохраним его как Е 11. Далее на листе необходимо выполнить заголовок расчета:

«Линейная интерполяция». Далее форматируем столбики как описано @002. @003. @004. @004А.

Выполняем защиту столбиков и сохраняем лист как Е 11. Затем сохраняем как Е 11_Z.

Проверим форматирование столбиков и защитим лист @007.

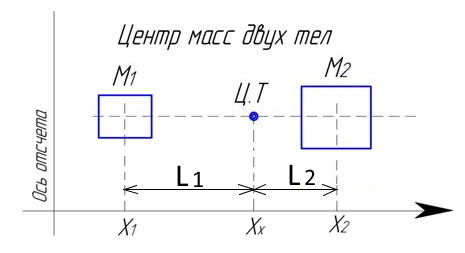
Расчет центра масс

Исходные данные:

Масса первого тела М1 = 6;

Масса второго тела М2 = 8;

От оси до центра массы первого тела Х1 = 4;

От оси до центра массы второго тела Х2 = 14;

Рис. Центр масс.

…

….

Расчет:

От оси до центра массы системы двух тел:

Рассчитываем как моменты масс относительно Оси отсчета Хх.

(L1+L2)=( X2-X1)= 10.. L1=(L1+L2)/((M1/M2)+1); L1=10/((6/8)+1).. ;

L1 = 5,7142857 … L2=4,285714..

Суммарная масса системы двух тел:

M=m1+m2; M= 6 + 8;.. M= 14 …

Проверка: М1*L1=M2*L2… 6*5,7142857=8*4,285714.. Равенство соблюдается..

( M1+M2)*(X1+L1)=(M1*X1)+(M2*X2).. (6+8)*(4+5,7142857)=(6*4)+(8*14)..

Равенство моментов соблюдается..

,,,,

Запись программы в Excel.

Первым делом откроем лист Excel по имени Е_10. ( Скачать из приложения ).

Сохраним его как Е 12. Далее на листе необходимо выполнить заголовок расчета:

«Центр масс двух тел». Далее форматируем столбики как описано @002. @003. @004. @004А.

Выполняем защиту столбиков и сохраняем лист как Е 12. Затем сохраняем как Е 12_Z.

Проверим форматирование столбиков и защитим лист @007.

Расчет геометрии многогранника

Многогранник:

Описанный диаметр d.

Вписанный диаметр dv.

Ширина грани L.

Угол между вершинами U.

Исходные данные:

Описанный диаметр d = 100…

Вписанный диаметр dv = 80,90169943749474.

Число граней многогранника n = 5…

Рис. Пятигранник.

Расчет:

Половина угла на грань:

Ur = 180 / n; Ur = 180 / 5; Ur = 36…

Расчет при известном описанном диаметре.

Радиус описанного диаметра:

R=d / 2; R=100 / 2; R= 50…

Радиус вписанной окружности:

Rv=(d/2)*cos( Ur ); Rv= 50 * cos( 36 );

Rv= 40,45084972…

Вписанный диаметр:

.dv=Rv+Rv; .dv= 40,45084972 + 40,45084972;

.dv= 80,90169944…

Максимальный размер между вершинами:

X = d * ( cos ( 90 / n ))…

Ширина грани:

Sg= 2*(sqrt( R * R – Rv * Rv )); Sg= 2*(sqrt( 50 * 50 – 40,45084972 * 40,45084972 ));

Sg= 58,77852523…

Площадь многогранника:

S= ( Sg * Rv * n ) / 2; S= ( 58,77852523 * 40,45084972 * 5 ) / 2; S= 5944,103227…

Запись программы в Excel.

Первым делом откроем лист Excel по имени Е_12. ( Скачать из приложения ).

Сохраним его как Е 13. Далее на листе необходимо выполнить заголовок расчета:

«Геометрия многогранника». Далее форматируем столбики как описано @002. @003. @004. @004А.

Расчеты: Здесь много расчетов связанных с углами. Компьютер угловые функции ведет в радианах.

@010. Угол 180 градусов равен числу Pii = 3,1415926 радиан..

Перевод из градусов в радианы: Радианы = Градусы*Pii/180…

Перевод из радиан в градусы: Градус = Радиан*180/Pii…

Любая тригонометрическая функция требует ввода аргумента в радианах.

Аргумент следует предварительно рассчитать и в функцию вставить адрес ячейки с аргументом.

Формулы приведены выше и в Excel. Можно посмотреть в открытом листе Е13.

Выполняем защиту столбиков и сохраняем лист как Е 13. Затем сохраняем как Е 13_Z.

Проверим форматирование столбиков и защитим лист @007.

Геометрия коробовой кривой ( овала )

Коробовая кривая – этой кривой можно с достаточной точностью заменить овальную кривую.

К примеру с помощью программы расчета геометрии коробовой кривой можно рассчитать геометрические размеры обжатого уплотнительного круглого резинового кольца.

Рис. Коробовая построение.

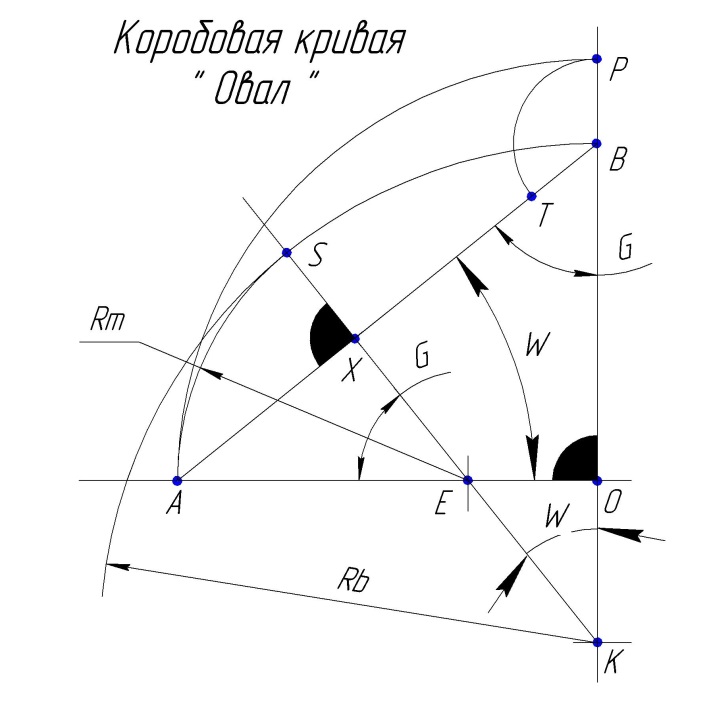
Построение:

Задано:

Большая полуось ОА… ОА = ОP..

Малая полуось ОВ.

Алгоритм Расчета:

ОА = ОP.. Построением..

Построением: РВ = ОА – ОВ; ТВ = РВ..

АВ =sqrt( АО*АО + ОВ*ОВ ); АТ = АВ – ТВ; ХТ = АТ / 2;

Из подобия треугольников: АХ / АО = АE / АВ; отсюда:

АE = АХ*АВ / АО; аналогично: ВК = ( АХ + ВТ )* АВ / ВО;

ОE = ОА – АE; ОК = ВК – ОВ; ХВ = ХТ + ТВ = AX + BT;

Rm=(XT*AB)/OA.. Малый радиус..

Rb=BK=(AB*(XT+PB))/OB… Большой радиус..

X=OB/OA..

UA=ATan(X).. Угол большого круга..

UB=(Pii/2)-UA… Угол малого круга..

SB=Pii*BK*BK.. Площадь круга с больш.R..

SM=Pii*Rm*Rm.. Площадь круга с малым .R..

SBS=SB*2*UA/Pii..

SMS=SM*2*UB/Pii..

KO=BK-OB..

OO1=OA-Rm..

STR=2*KO*OO1..

SO=(SMS+SBS)-STR..

XU=UA*360/Pii..

X=4*SO/Pii..

DS= sqrt(X)..

Для расчета площади сечения коробовой кривой :

Большой радиус Rb = КВ; Зная стороны ВК и ХВ – находим угол сектора «W».

Зная радиус Rb и угол сектора «W»– найдем площадь сектора.

Зная стороны ОК и ОE прямоугольного треугольника – найдем его площадь

и вычтем из площади сектора радиуса Rb.

Малый радиус Rm = EА; Зная угол «W»прямоугольного треугольника КХВ

определяем угол сектора малого радиуса как:

G = 90 – W; Далее: определим площадь сектора малого радиуса.

Площадь сечения коробовой кривой найдена.

Найдем диаметр круга равный по площади заданной коробовой кривой:

.d =sqrt( 4*S / Pii ); Где S – площадь заданной коробовой кривой.

Контрольный расчет:

Дано:

Большая ось = 80; Малая ось = 60;

Рис. Коробовая радиусы.

….

….

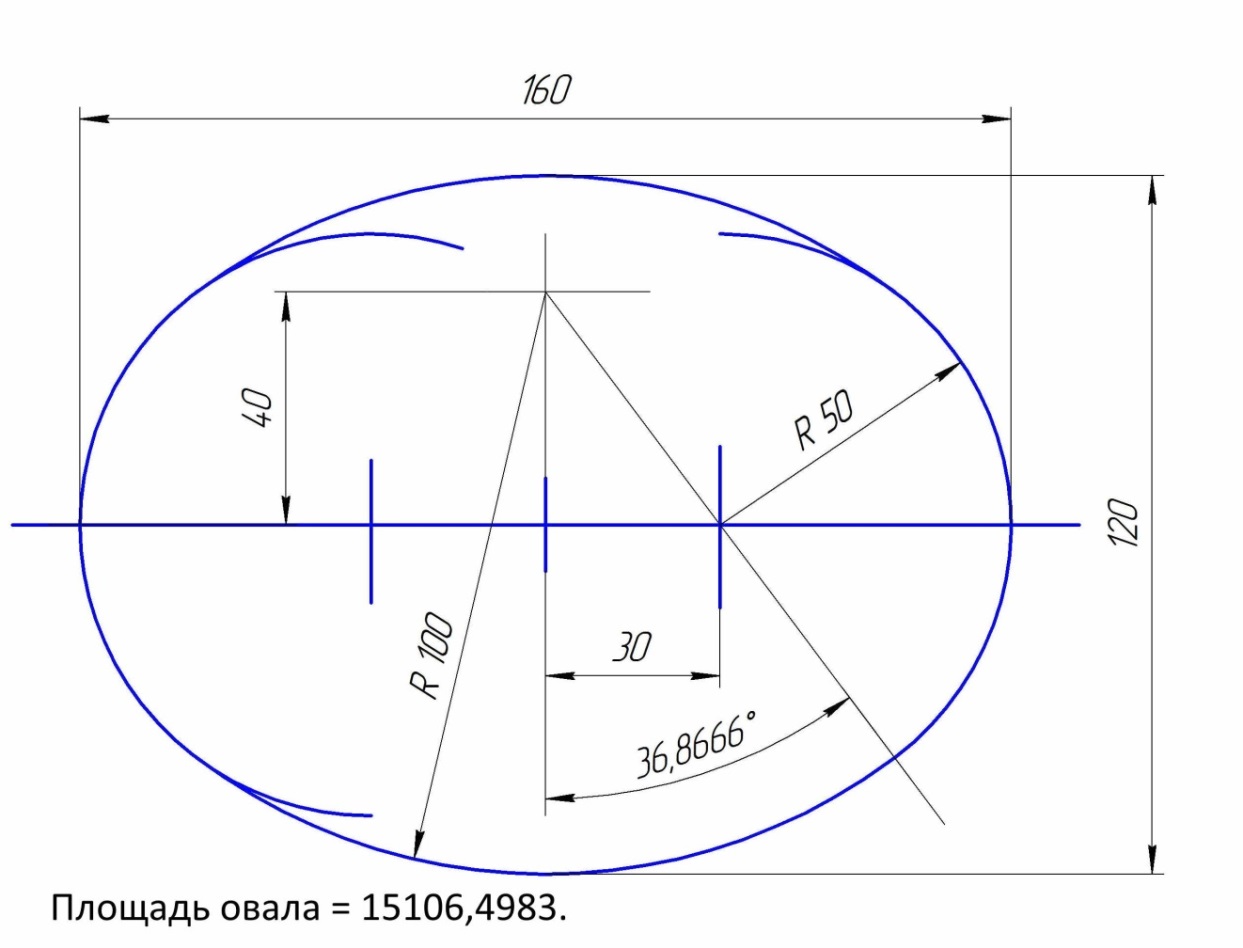
Расчет:

Больший радиус = 100,0..

От оси до центра Б. радиуса = 40,0..

Меньший радиус = 50,0..

От оси до центра M. радиуса = 30,0..

Угол раствора Б. радиусов = 73,739795..

Площадь ограниченная коробовой кривой = 15106,498;

Диам. Круга равной площади = 138,687;

Запись программы в Excel

Первым делом откроем лист Excel по имени Е_12. ( Скачать из приложения ).

Сохраним его как Е 14. Далее на листе необходимо выполнить заголовок расчета:

«Геометрия овала». Далее форматируем столбики как описано @002. @003. @004. @004А.

Расчеты: Здесь много расчетов связанных с углами. Компьютер угловые функции ведет в радианах.

@010. Угол 180 градусов равен числу Pii = 3,1415926 радиан..

Перевод из градусов в радианы: Радианы = Градусы*Pii/180…

Перевод из радиан в градусы: Градус = Радиан*180/Pii…

Любая тригонометрическая функция требует ввода аргумента в радианах.

Аргумент следует предварительно рассчитать и в функцию вставить адрес ячейки с аргументом.

Формулы приведены выше и в Excel. Можно посмотреть в открытом листе Е14.

Все расчеты проведены в столбике «F»так как много промежеточных расчетов.

Итоговые результаты выведены в столбик результатов «D».

Рисунок вставляем в лист, как описано в @013.

Выполняем защиту столбиков и сохраняем лист как Е 14. Затем сохраняем как Е 14_Z.

Проверим форматирование столбиков и защитим лист @007.

Геометрия радиусной кривой

Все расчеты по разным вариантам исходных данных:

Хорда L; Прогиб Н; Радиус R; Угол G.

Эти расчеты часто требуются для нахождения элементов детали имеющих форму сегмента окружности.

Рис. Геометрия радиусной кривой.

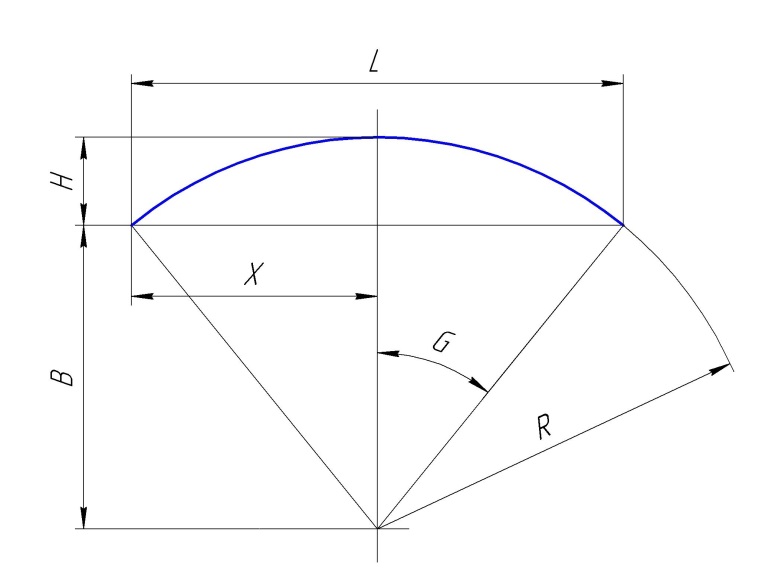
Расчет производим из следующих соотношений:

В = sqrt( R*R – X*X); L = X + X; H = R – B; G = аrcsin ( X / R );

Длина дуги = Pii * R * G / 90;

Площадь сектора Ss = Pii * R * R * G / 180;

Площадь треугольника под хордой St = L * B /2;

Площадь сегмента ( горбушки ) Sg = Ss – St;

Некоторые комбинации данных не позволяют прямого расчета,

тогда применяем метод компьютерного подбора.

Контрольный расчет:

Радиус R = 1000;

Диаметр D = R+R; D = 2000; Хорда L = 765,3668647;

Стрела прогиба максимальная H = 76,12046749;

Угол: Центр – Хорда: 2 * G = Au = 45 градусов..

Площадь сектора круга с углом = Au:

Sk=Pii*D*D* Au /(4*360); Sk = 392699,0816987241;

Площадь треугольника в секторе:

St=(L/2)* B; St = 353553,3905932738;

Площадь горбушки отсеченной хордой:

S = Sk-St; S = 39145,69110545033;

Длина дуги над хордой:

L=Pii*D*Au /360; L = 785,3981634;

Запись программы в Excel.

Первым делом откроем лист Excel по имени Е_12. ( Скачать из приложения ).

Сохраним его как Е 15. Далее на листе необходимо выполнить заголовок расчета:

«Геометрия радиусной кривой.». Далее форматируем столбики как описано @002. @003. @004. @004А.

Далее как в предыдущем.

Примечание: При исходных данных «Хорда – Прогиб» прямым расчетом не решается – применяем метод подбора с шаговым уточнением. В Excel програмные циклы запрещены – поэтому автоматический подбор запрограммировать не получится. Такие программы делаем в Python..

Координаты радиусной кривой

Построение части окружности методом подъема применяется тогда, когда радиус слишком велик

для традиционного построения, либо когда точка центра радиуса недоступна.

Если внутри контура кривой расположены объекты мешающие построению хорды, тогда строят линию, паралленьную хорде, с точкой касания в вершине кривой и от этой линии откладывают величины «Н2».

Рис. Координаты радиусной кривой.

,,,,

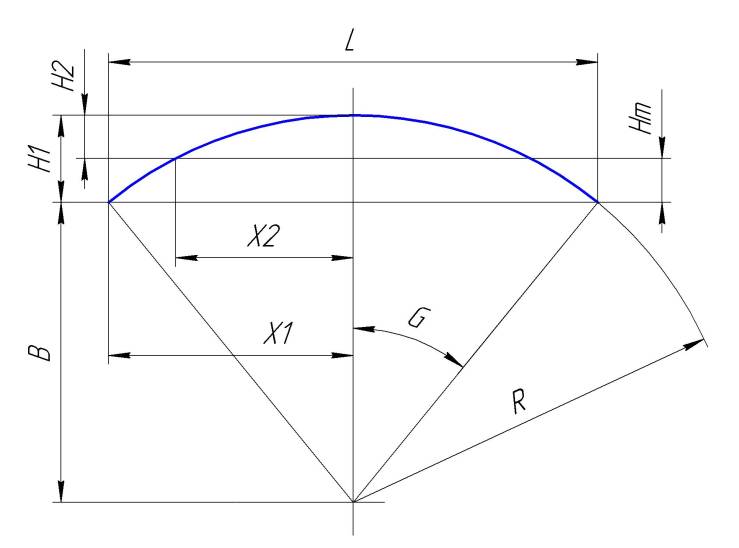
Построение части окружности методом подъема.

Построение:

Задаем максимальный размер хорды L.

Из середины максимальной хорды L строим перпендикуляр Н1.

Х1 = L / 2; В = sqrt( R*R – X1*X1); H1 = R – B;

Определили максимальную стрелу прогиба кривой H1.

Далее задаем произвольное расстояние от центральной оси Х2.

Находим стрелу прогиба Н2 = R – ( sqrt( R*R – X2*X2));

Находим высоту подъема в точке Х2: Hm = H1 – H2;

Задавая ряд текущих значений Х2 и рассчитывая соответствующие высоты подъема Hm

– получаем достаточное количество точек,

для построения радиусной кривой по точкам на этой кривой.

Контрольный расчет:

Исходные данные:

Радиус R = 10000;

Хорда максимальная заданная L = 8000;

Подъем максимальный в центре хорды = 834,8486100883201.

Задаем ряд точек:

От центра хорды до точки по оси Х-Х = 3000,0.

Величина подъема ( перпендикуляра ) = 374,2406242577763.

…

От центра хорды до точки по оси Х-Х = 2000,0.

Величина подъема ( перпендикуляра ) = 632,8075812210318.

…

От центра хорды до точки по оси Х-Х = 1000,0.

Величина подъема ( перпендикуляра ) = 784,7229811545203.

…

От центра хорды до точки по оси Х-Х = 500,0.

Величина подъема ( перпендикуляра ) = 822,3407878074104.

…

От центра хорды до точки по оси Х-Х = 0,001.

Величина подъема ( перпендикуляра ) = 834,848610088271.

Запись программы в Excel.

Первым делом откроем лист Excel по имени Е_15. ( Скачать из приложения ).

Сохраним его как Е 16. Далее на листе необходимо выполнить заголовок расчета:

Остальное аналогично предыдущему, формулы приведены выше, записи в Excel смотрите в открытом

Листе – скачать в приложении.

Расчет геометрии треугольника

Напротив сторон треугольника лежат одноименные углы.

Рис. Геометрия треугольника.

,,,

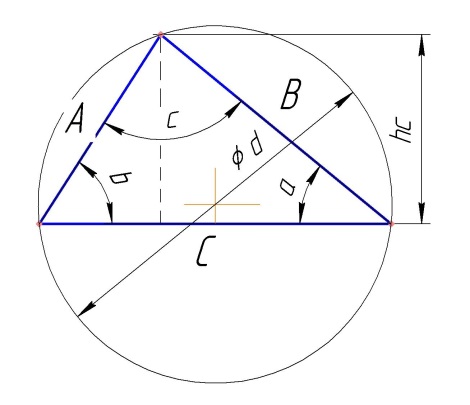
Известны три стороны треугольника

Напротив сторон треугольника лежат одноименные углы.

Сторона = a. Сторона = b. Сторона = c.

Решение:

.x=((b*b)+(c*c)-(a*a))/(2*b*c)… au=аrccos(x)… Угол А.

.x=((a*a)+(c*c)-(b*b))/(2*a*c)… bu=аrccos(x)… Угол В.

.cu=180-(au+bu)… Угол С.

Известны две стороны и угол между ними

Сторона = a; Сторона = b; Угол = cu..

Решение:

.с= sqrt ((a*a)+(b*b))-(2*a*b*(cos(cu)))… Сторона «с».

.x=((b*b)+(c*c)-(a*a))/(2*b*c)… au=arccos(x)… Угол А.

.x=((a*a)+(c*c)-(b*b))/(2*a*c)… bu=arccos(x)… Угол В.

Известны два угла и сторона между ними

Сторона = a; Угол = bu; Угол = cu;

Решение: .au=180-(bu+cu)… Угол А. .b=(a*(sin(bu)))/(sin(au))… Сторона В.

.c=(b*(sin(cu)))/(sin(bu))… Сторона С.

Добавочный расчет в алгоритм Треугольника

Решение:

R=a/(2*(sin(au))… R – Радиус описанной окружности.

.hc=b*(sin(au))… Высота из угла С.

.hb=a*( sin(cu))… Высота из угла B.

.ha=c*(sin(bu))… Высота из угла A.

S=a*ha/2.. Площадь треугольника.

Pe=a+b+c.. Периметр.

.rv=(S+S)/Pe… Радиус вписанной окружности.

…..

Контрольный расчет:

Напротив сторон треугольника лежат одноименные углы.

Сторона А = 15,77350269;

Сторона В = 14,14213562;

Сторона С = 11,54700538;

Угол А = 75; Угол В = 60; Угол С = 45..

Высота А= 10; Высота В = 11,1535507;

Высота С = 13,66025403;

Описанный радиус = 8,164965804;

Вписанный радиус = 3,804268442;

Площадь = 78,86751346;

Запись программы в Excel.

Смотри открытый и закрытый листы Е 17.. ( Скачать из приложения ).