
Сергей Фёдорович Гаврилов
Расчеты конструктору
Находим момент инерции каждого прямоугольника относительно оси
проходящей через общий центр тяжести.
Находим общий для системы момент инерции и общую площадь.
Рассчитанную систему принимаем как первый прямоугольник.
Добавляем еще один прямоугольник и повторяем выше приведенный расчет.
Этот цикл расчетов ведем, пока не просчитаем все прямоугольники произвольного сечения.
Высота первого прямоугольника = h.
Ширина первого прямоугольника = b.
.j1=b*h*h*h/12… Момент инерции первого прямоугольника.
.w1=j1/(h/2)… Момент сопротивления первого прямоугольника.
.s1=h*b… Площадь сечения первого прямоугольника.
.xc1=h/2… Высота центра тяжести первого прямоугольника от оси Х-Х.
.m1=s1*(h/2)… Момент площади первого прямоугольника относительно оси Х-Х.
# Точка расчета № 1…
Высота второго прямоугольника = h1.
Ширина второго прямоугольника = b1.
Высота расположения основания
второго прямоугольника относительно оси Х-Х = hx.
.j2=b1*h1*h1*h1/12… Момент инерции второго прямоугольника.
.w2=j2/(h1/2)… Момент сопротивления второго прямоугольника.
.s2=h1*b1… Площадь сечения второго прямоугольника.
.xc2=(h1/2)+hx… Высота центра тяжести второго прямоугольника от оси Х-Х.
.m2=s2*((h1/2)+hx)… Момент площади второго прямоугольника относительно оси Х-Х.
.xx=(m1+m2)/(s1+s2)… Расстояние Ц.Т. от оси Х-Х системы двух прямоугольников.
R1=xx-xc1… Расстояние между Ц.Т. системы и Ц.Т. первого прямоугольника.
R2=xc2-xx… Расстояние между Ц.Т. системы и Ц.Т. второго прямоугольника.
.j1x=j1+( R1*R1*s1)…Момент инерции первого прямоугольника относительно Ц.Т. системы.
.J2x=j1+( R2*R2*s2)…Момент инерции второго прямоугольника относительно Ц.Т. системы.
.Jx=j1x+j2x… Момент инерции системы двух прямоугольников относительно Ц.Т. системы.
Sx=s1+s2… Суммарная площадь двух прямоугольников.
.... .....
Далее в расчете принимаем систему двух прямоугольников за новый, первый прямоугольник у которого:
.s1=Sx… xc1=xx… j1=Jx… m1=Sx*xx…
Вводим данные следующего прямоугольника:
( считая его новым вторым прямоугольником ) и снова проходим весь расчет,
начиная с # Точки расчета № 1…
Для проверки можно пересчитать сечение « Рельс ».
……..
Кстати все вышеизложенные расчеты эффективнее выполнять используя программы.
Программы можно скопировать из книги « Python 3 Полезные программы книга третья. ».
Программы значительно экономят время и уменьшают вероятность ошибок в расчетах..
Программы можно выполнить так же в Excel.
,,,,
Разные расчеты элементов деталей машин.
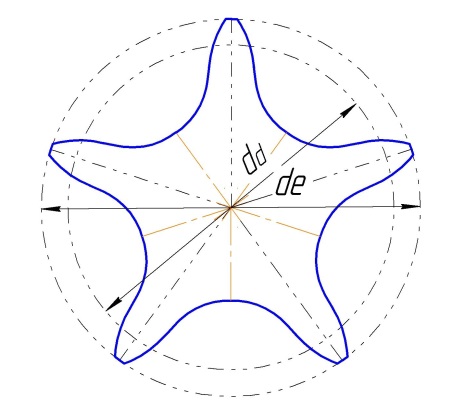
Расчет параметров профиля звездочки по ГОСТ 591-69.
Для примера построения принимаем нестандартные исходные данные:
Число зубьев звездочки = 5..
Шаг цепи = 50 …
Диаметр ролика цепи = 36 ..
…… …….. …….
Расчет лучше производить по программе.
В программе использовать формулы из ГОСТ 591-69..
….
Построение профиля зуба проводим в следующем порядке:
Строим диаметр окружности выступов de = 98,819..
Строим диаметр делительной окружности dd = 85,065..
От вертикальной осевой вправо и влево откладываем размеры по = 0,5 е.
Е = 1,5 .. 0,5 е = 0,75 .. Проводим вспомогательные осевые параллельные вертикальной осевой.
Левая вспомогательная осевая при пересечении с делительной окружностью создает точку « О ».
Из этой точки проводим радиус впадины R = 18,14 …
Через точку « О » проводим прямую перпендикулярную вертикальной осевой.
От этой прямой отмеряем размер « Y 2 » вниз и « Y 1 » вверх от прямой.
От левой вспомогательной осевой влево отложим размер « Х 2 ». Пересечение линий « Y 2 » и « Х 2 » даст центр радиуса R 2 = 26,178 – радиуса головки зуба ( центр – точка « О2 » ). Пересечение линий « Y 1 » и
« Х 1 » даст центр радиуса R 1 = 46,94 – радиуса сопряжения радиусов R и R 2 ( центр – точка « О1 » ). Точки сопряжения находятся на прямых линиях проходящих через точки центров сопрягаемых радиусов. ( точки « Е » и « F » ). Из центра окружностей проводим луч с отклонением на половину углового шага зубьев звездочки. При заданном числе зубьев = 5 .. отклонение = 36 градусов. Построенная часть зуба симметрична относительно этого луча.
Исходные данные:
Число зубьев звездочки z = 5..
Шаг цепи t = 50 …
Диаметр ролика цепи d = 36 ..
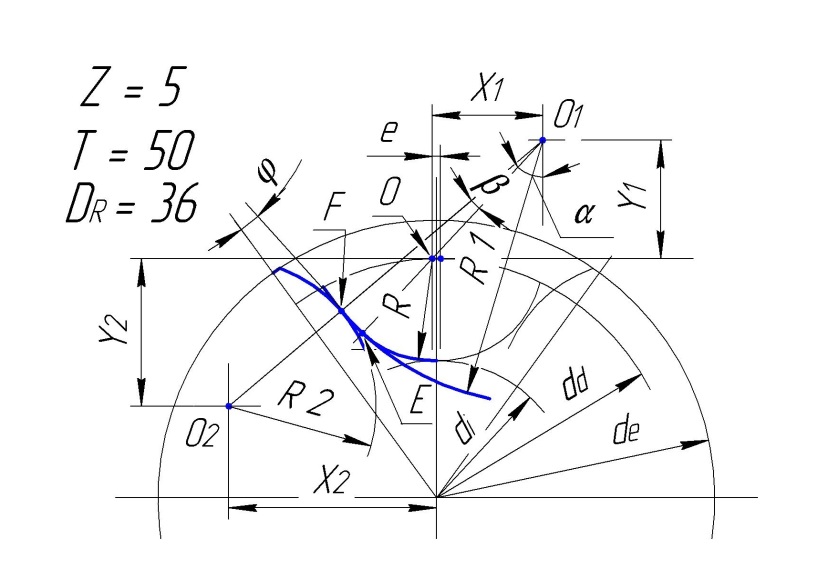
Расчет:
Все в градусах и миллиметрах.
.ddo=t /(sin(180/z))… Делительный диаметр звездочки.
.dn=t*(0,6+(tan(90-(180/z ))))… Наружный диаметр.
.rv=(0,5025*d)+0,05… Радиус впадин
.di=ddo-(rv+rv)… Диаметр дна зубьев.
.r1=(0,8*d)+rv… Радиус сопряжения R1.
.uv=55-(60/z)… Половина угла впадины « а » в градусах.
.us=18-(56/z)… Угол сопряжения « b » в градусах.
.uf=90-((180/z)+uv+us)… Половина угла зуба « f » в градусах.
.e=0,03*t… Смещение центров дуг впадин « е ».
.x1=(0,8*d)*(sin(uv))… Координаты точки О1.
.y1=(0,8*d)*(cos(uv))… Координаты точки О1.
.x2=1,24*d*(cos(180/z))… Координаты точки О2.
.y2=1,24*d*(sin(180/z))… Координаты точки О2.
Радиус головки зуба R2:
.r2=(d*((1,24*(cos( uf )))+(0,8*(cos( us )))-1,3025))-0,05…
…
.ctg( a ) = tan ( 90 – a )… Перевод приведен для справки..
Контрольный расчет:
Задано:
Число зубьев звездочки = 5,0.
Шаг цепи = 50,0.
Диаметр ролика цепи = 36,0.…
Диаметр делительной окружности = 85,065081.
Диаметр окружности выступов = 98,819096.
Диаметр окружности впадин = 48,78508084.
…
Радиус впадин = 18,14.
Радиус сопряжения R1 = 46,94.
Радиус головки зуба R2 = 26,17752.
Половина угла впадины ( угол альфа ) = 43,0.
Угол сопряжения бета = 6,80.
Половина угла зуба ( угол фи ) = 4,20.
Смещение центров дуг впадин E = 1,5.
Координаты точки О 1:
Координата Х 1= 19,64155.
Координата Y 1 = 21,0629866.
Координаты точки О 2:
Координата Х 2 = 36,1145186.
Координата Y 2 = 26,23873.
…….
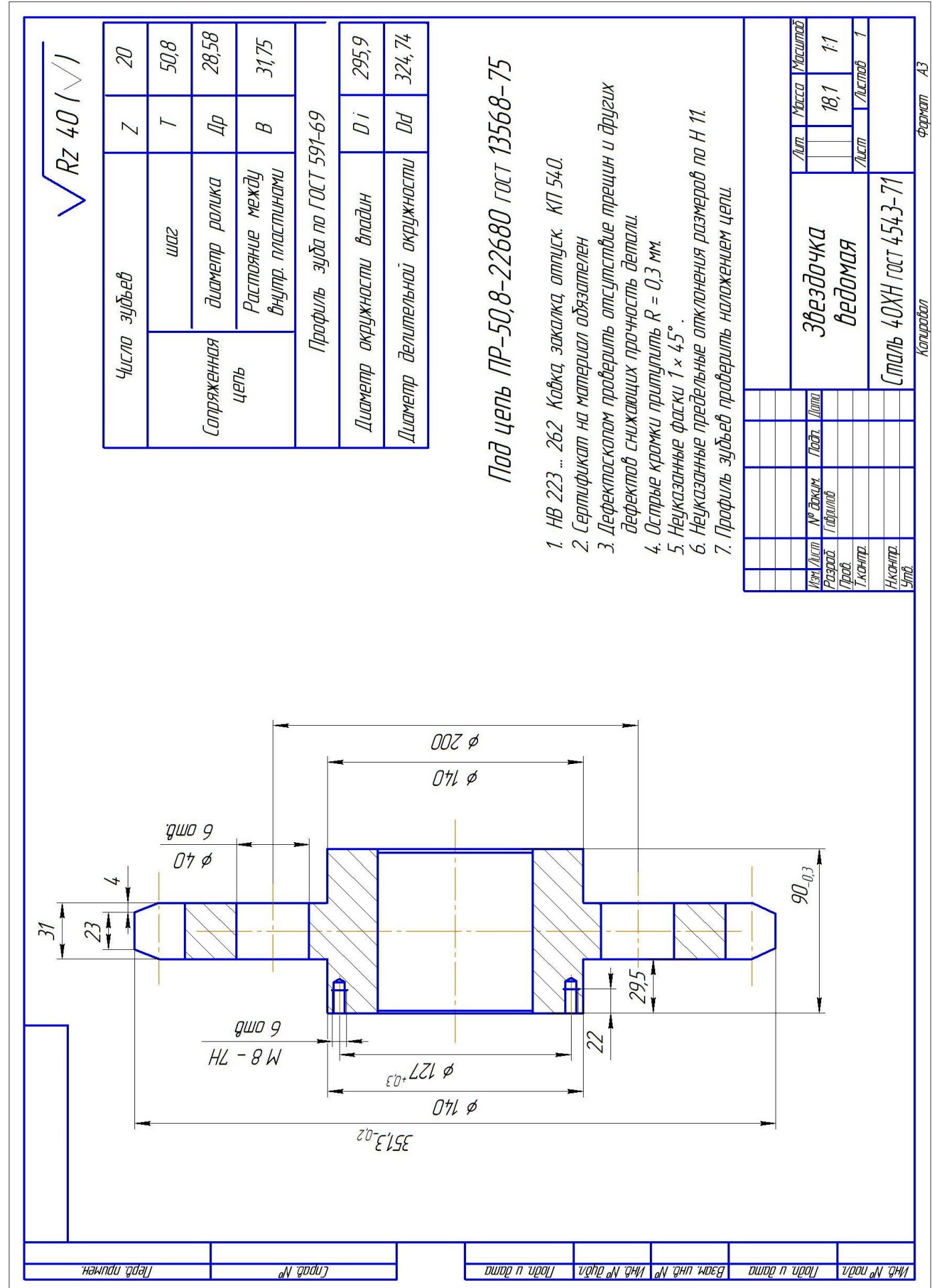
Чертеж приведен для примера. Важно добавить в тех.условиях « Профиль зуба проверить наложением цепи. ».
Прорисовку профиля зуба с размерами профиля на чертеже делают только по требованию цеха – изготовителя. Обычно достаточно указать « профиль звездочки по ГОСТ 591-69. » и ГОСТ и марку цепи.
## « Чертеж звездочки » Ссылка:
Ссылка Studenty.zip : https://disk.yandex.ru/d/orKSVHysYSMK0Q
Studenty.zip : CRC 32 = 77d05e10… Объем -= 77,916,434....
……..
Ссылка Студенту.zip : https://disk.yandex.ru/d/Rbo3M49TP3xMdg
Студенту.zip: CRC 32 = E76A2853… Объем -= 152458350…
…..
В браузере, в адресной строке удалить адрес, который там стоял и вставить скопированный адрес ссылки.
Щелкнуть по ссылке – подтвердить « Посетить ». На странице Яндекс диска нажать « Скачать » « Сохранить ».
Затем – Показать ход загрузки. Браузер пишет « Обычно такие файлы не скачиваем ». Щелкаем правой клавишей мыши – командуем « Разрешить загрузку ». Файл загружается в стандартную папку « Загрузки ».
Для контроля проверить размер файла и CRC32.. Затем распаковать в свою папку.
Расчет CRC32 по программе HashTab_v6.0.0.34 …https://hashtab.ru/…
Расчет пружины сжатия.
Для примера приведен рабочий чертеж пружины сжатия:
Наружный диаметр = 48 мм.
Диаметр проволоки = 6 мм.
Шаг витков = 12 мм.
Свободная длина = 124 мм.
Макс. нагрузка = 100 кгс.
Осадка под макс. нагр. = 56 мм.
…
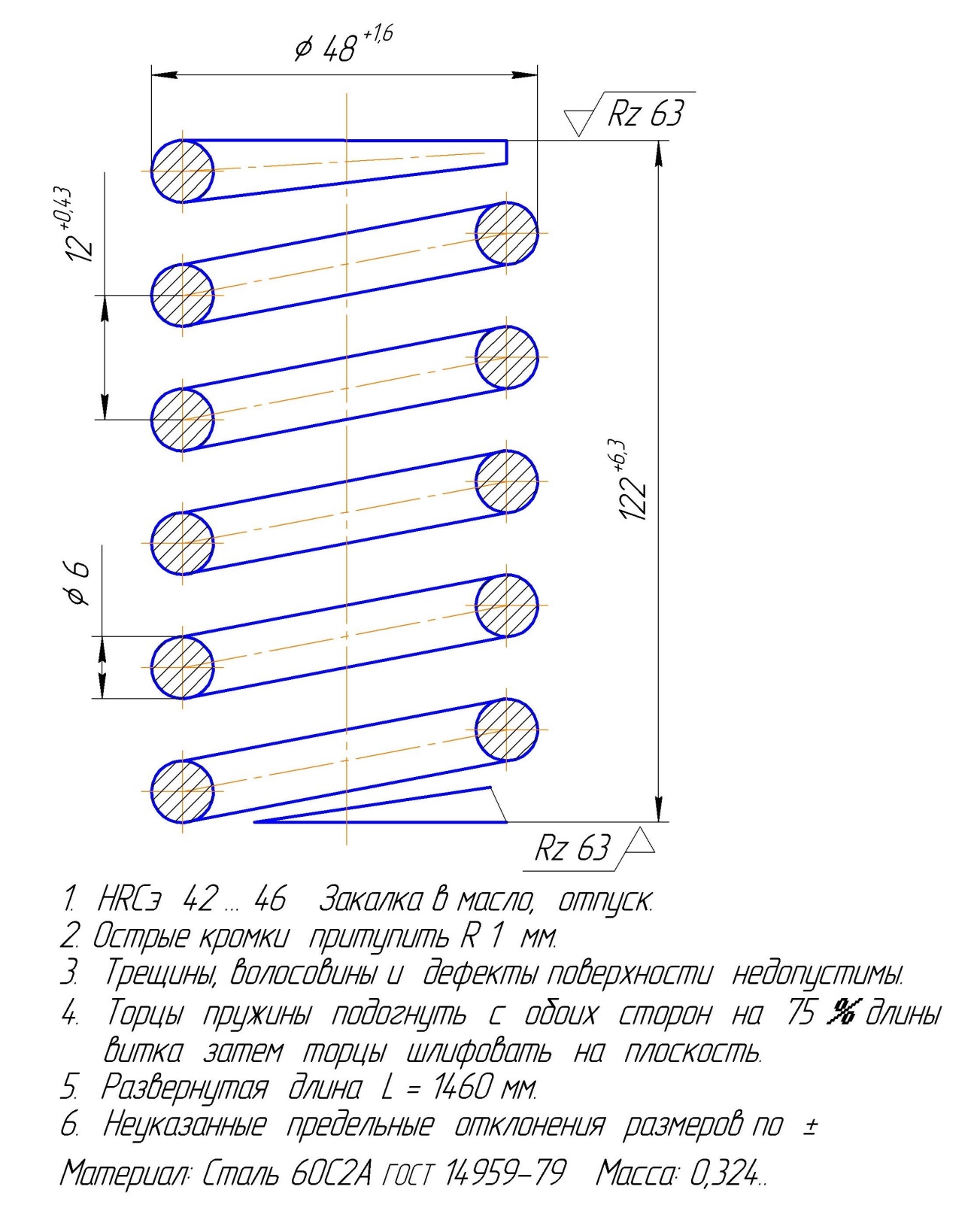
Выполним проверочный расчет пружины сжатия:
Расчет пружины сжатия ( проверочный ).
Пружины сжатия различают по классам:
Первый класс – циклическая нагрузка на Пять миллионов циклов.
( по Анурьеву выпуска 2001 г. – Десять миллионов циклов ).
Выполняют из сталей 60С2А и 65С2ВА ГОСТ 14963-69 HRC 46 … 52.
и из стали 50ХФА ГОСТ 14963-69 HRC 44 … 50.
допускаемое касательное напряжение для этих сталей не более 56 кгс/кв.мм.
Второй класс – циклическая нагрузка на Сто тысяч циклов.
Стали те же самые, HRC без изменений – ( напряжение увеличено ).
Допускаемое касательное для этих сталей в этом классе не более 96 кгс/кв.мм.
Соударения витков для этих классов не допускается.
Третий класс – циклическая нагрузка на Две тысячи циклов.
Стали те же самые, HRC 53 … 57 – ( напряжение увеличено ).
Допускаемое касательное для этих сталей в этом классе не более 135 кгс/кв.мм.
Все размеры в расчете в миллиметрах – материал – сталь : плотность q = 7,95 т/куб.м.
…………
Расчет параметров пружины сжатия
Исходные данные:
Наружный диаметр пружины d = 48..
Диаметр проволоки пружины dp = 6..
Шаг навивки пружины tp = 12..
Полный ход пружины до выборки зазоров между витков ws = 56..
Рабочее усилие на пружину p2 = 100 кгс..
.....
Расчет:
.do=d-dp… Средний диаметр.
.z=dp*dp*dp*dp*1000/(do*do*do)… Жесткость одного витка..
Жесткость одного витка z = 17,4927 кгс/мм.
.c=do/dp…
.k=(((4*c)-1)/((4*c)-4))+(0,615/c)…
Коэф. К = p1=(tp-dp)*z … Gsf = 461030/2725231222…|
Усилие при полном сжатии одного витка p1 = 104,9563 кгс.
.tk=8*k*p1*do/(Pii*dp*dp*dp)…
Касательное напряжение при полном сжатии витка tk = 63,0309 кгс/мм2 .
.tk1=8*k*p2*do/(Pii*dp*dp*dp)…
Касательное напряжение при рабочем усилии tk1= 60,0545 кгс/мм2 .
L1v=p2/z…
Деформация одного витка при рабочем усилии L1v = 5,7167 мм.
.с = sqrt ((Pii*do*Pii*do)+(tp*tp))… Квадрат гипотенузы.
Вариант № 1.
Пружина с подогнутыми витками – но без подшлифовки крайних витков.
.w=(ws/(tp-dp))+3…
Число витков полное c учетом подогнутых витков w = 12,3333…
.ll=((w-3)*tp)+(3*dp)…
Свободная габаритная длина пружины ll = 130,0 мм.
.llr=c*w…
Развернутая длина проволоки пружины llr = 1634,06 мм.
.s=Pii*dp*dp/4…
.px=7,95*s*llr/1000000…
Вес пружины px = 0,367 кг.
.....
Вариант № 2.
Пружина с подогнутыми крайними витками,
крайние витки сошлифованы на плоскость перпендикулярную оси пружины.
.we=(ws/(tp-dp))+2 …
.lle=((w-3)*tp)+(2*dp)…
.llre=c*we …
Число витков полное ( с подогнутыми витками ) we = 11,3333…
Свободная габаритная длина пружины lle = 124,0 мм.
Развернутая длина проволоки пружины llre = 1501,57 мм.
.se=Pii*dp*dp/4…
.pxe=7.95*se*llre/1000000…
Вес пружины pxe = 0,338 кг.
Все размеры в миллиметрах – материал – сталь q = 7,95 т / м3
…..
Примечание:
При мелкосерийном производстве точно определить число рабочих витков,
длину пружины под нагрузкой не получится, так как подгиб концевых витков выполняется
с большими отклонениями по размеру.
Пружину в единичном производстве обычно навивают на цилиндр равный внутреннему диаметру пружины.
Цилиндр зажимают в патрон токарного станка, один конец проволоки прочно прикрепляют к цилиндру.
Другой конец проволоки проходит через поводок закрепленный в резцодержателе станка.
Станок включают на нарезание резьбы с шагом навивки пружины. Скорость шпинделя 20..60 об/мин.
Направление вращения – обратное ( при взгляде от суппорта – по часовой стрелке ) при ходе суппорта от патрона. Количество витков делают больше чертежного минимум на два витка для подгонки.
Навив пружину – не ослабляя усилие на проволоку – надежно закрепляют второй конец проволоки на цилиндре.
Затем проводят полную термообработку пружины в сборе с цилиндром ( закалку и отпуск ).
Для не ответственных узлов применяют Проволоку стальную углеродистую пружинную ГОСТ 9389-75.
Холоднотянутую проволоку, применяемую для изготовления пружин, навиваемых в холодном состоянии
и не подвергаемых закалке. При навивке такой пружины следует учитывать, что при снятии усилия навивки –
пружина разворачивается, увеличивая шаг навивки и наружный диаметр.
Кольцевая пружина.
Применяется в буферных устройствах для гашения ударов и вибраций.
А так же кольцевая пружина применяется для предохранения анкерных шпилек от перегрузок,
Для примера рассчитаем кольцевую пружину анкерного болта подверженного ударным нагрузкам.
Материалы пружин: Наиболее прочная Сталь 60С2Н2А ГОСТ 14959-79.
Первый класс – циклическая нагрузка на Пять миллионов циклов.
( по Анурьеву выпуска 2001 г. – Десять миллионов циклов ).
Типовое решение из сталей 60С2А и 65С2ВА ГОСТ 14963-69 HRC 46 … 52..
и из стали 50ХФА ГОСТ 14963-69 HRC 44 … 50..
допускаемое касательное для этих сталей не более 56 кгс/кв.мм.
Применим сталь 60С2А ГОСТ 14959-79. Предел текучести 143 кгс/кв.мм.
Предел прочности 163 кгс/кв.мм. Ресурс принимаем = 5000000 циклов.
Допускаемое напряжение на растяжение Вд = 9600 кгс / кв.см.
Закалка с 870 градусов в масло затем отпуск с 420 градусов..
Рассчитываем наружное кольцо пружины при работе испытывающей напряжения
растяжения. Внутренняя пружина испытывает напряжения сжатия – что менее опасно.
Величины напряжений и деформация при равенстве поперечных сечений одинаковы.
Поэтому внутреннее кольцо считать не будем.
Эскиз сечения наружного кольца пружины.
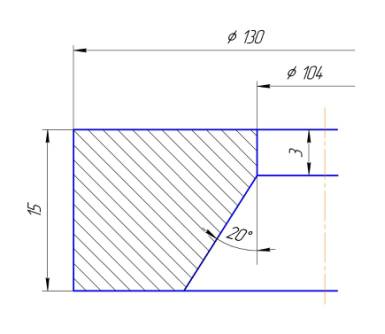
Кольцевая пружина – внешнее кольцо.
Pii = 3,1415926 … Число Пи…
Е = 2000000 кгс / кв.см. Модуль упругости стали..
Максимальное осевое усилие вдвигающее конус в коническую расточку кольца принимаем равной:
Q = 20000 кгс. При силе ударной нагрузки на шпильку равной Qот = 9472 кгс.
Предполагаемый коэф. трения на конусе: Ктр = 0,1.. ( вибрация уменьшает трение)..
Угол трения: Gt = arctan ( 0,1 )… Gt = 5,6666666º… ( градусов ).
Наружный диаметр кольца: Ф = 130 мм.
Внутренний цилиндрический участок: Фв = 104 мм. Длина Lв = 3 мм.
Полная высота кольца пружины L = 15 мм.
Коническая расточка внутреннего диаметра:
Угол: Образующая – Ось кольца: G = 20º.. Высота расточки Lк = 12 мм.
Наибольший диаметр расточки: Фк = ( Lк × 2 × ( tan 20º )) + Фв.. Фк = 112,7353 мм.
Площадь поперечного сечения кольца пружины: S = 1,68794 кв.см.
Объем кольца пружины: V = 62,8739 куб.см.. Масса = 0,49356 кг…
Средний диаметр кольца пружины: Фср = V / ( S × Pii )…
Фср = 62,8736 / ( 1,68794 × 3,1415926 ) .. Фср = 11,85662 см… Фср = 118,5662 мм.
Gsf = 461030/2725231222…
Так как угол трения значительно меньше угла конуса – при снятии нагрузки пружина
вернется в исходное положение.. При этом часть энергии израсходуется на трение на
конусе – поэтому колебания при снятии нагрузки быстро затухнут..
Удельное давление на кольцо при внедрении конуса:
.g = Q / ( Pii* Ктр*L* Фср*((0,34202/ Ктр)+0,9397)).. В.С. Поляков.
Где: 0,3420201 – синус 20 градусов. 0,9397 – косинус 20 градусов..
20 градусов – угол осевая – образующая конуса.
.g = 20000 / ( Pii* 0,1*1,5*11,85662 *4,36).. .g = 821 кгс/кв.см.
Расчет ведем по формулам для цилиндра под давлением. По Даркову.
Радиальное напряжение:
X=g*Rv*Rv/((Rn*Rn)-(Rv*Rv))..
Y=Rn*Rn/(Rv*Rv)..
Br=X*(1-Y).... # Радиальное напряжение.
Где: Rn = 6,5 см – Наружный радиус цилиндра.
Rv = 5,92831 см. – Внутренний радиус цилиндра.
# …
X=821*5,92831 *5,92831 /((6,5*6,5)-( 5,92831 *5,92831))…
X=4061…
Y=6,5*6,5/(5,92831 *5,92831)… Y=1,20217…
Br=4061*(1-1,20217).... Br= -821 кгс / кв.см… # Радиальное напряжение.
....
Тангенциальное ( растягивающее ) напряжение в кольце.
Bt=X*(1+Y).. # Тангенциальное напряжение.
Bt=4061*(1+1,20217 ) … Bt= 8943 кгс / кв.см… # Кольцо прочно…
# …
Развернутая длина кольца Ср = Фср * Pii.. Ср = 11,85662 * Pii.. Ср = 37,24867 см.
Удлинение средней линии при напряжении Вt = 8943 кгс/кв.см. по закону Гука:
.dL = Cр* Вt/Е.. dL = 37,24867 * 8943/2000000..
.dL = 0,1666 см.. или увеличение диаметра dФ = 0,053017 см.. dФ = 0,53017 мм..
Так как внутреннее кольцо сжимается на ту же величину,
то общее изменение диаметра dФ = 1,0603 мм.. Изменение радиуса:
.dR = 0,53017 мм. Осадка конуса под нагрузкой dH = dR/(tan 20).. dH = 0,53017 /0,36397..
.dH = 1,457 мм.. ( осадка пары конус – кольцо, без учета трения на конусе ).
Расчет производим по И.А. Биргеру. Стр. 173..
Тангенциальное ( растягивающее ) напряжение в кольце Вt = 8943 кгс / кв.см.
Что меньше допускаемого. Пружина будет более долговечна..
# ,,,,,,,
Проверим расчет исходя из заданной осадки конуса dH = 0,7285 мм..
( без учета сжатия внутреннего конуса и без учета трения на конусе ).
Изменение радиуса при осадке dR = dH * tg 20.. dR = 0,7285 * 0,36397..
.dR = 0,2652 мм. Изменение диаметра dd= 0,5303 мм.
Изменившийся средний диаметр Фсри = 118,5662+0,5303 = 119,0965 мм.
Изменившаяся длина окружности Ссри =118,90389 * Pii = 374,152704 мм.
Относительное изменение длины окружности Сотн = (Ссри–Ср) / Ср..
Сотн = (374,152704 –372,486703) / 372,486703.. Сотн = 1,666 / 372,486703..
Сотн = 0,00447265… Далее по закону Гука..
При таком относительном удлинении напряжение растяжения будет:
Врас = Е * Сотн… Врас = 2000000 * 0,00447265… Врас =8945,3 кгс/кв.см.
Для пружинной стали напряжение нормальное..
С учетом того, что коническая часть входящая в кольцо имеет равное кольцу
поперечное сечение т сожмется на ту же величину, то в целом осадка удвоится
и будет равной 1,457 мм.
# ,,,,,,
Тот же самый расчет по И.А. Биргеру. Но при коэф.трения = 0,01.. Gt = 0,57º…
Площадь поперечного сечения кольца пружины: S = 1,68794 кв.см.
Напряжение растяжения: Вр = Q / ( Pii*S*tan ( G + Gt ))…
Вр = 20000 / ( Pii*1,68794*tan ( 20 + 0,57 ))… Вр = 10048 кгс / кв.см.
Осадка конуса в кольцо пружины при приложении назрузки:
.dH = Q*Фср / ( 2*Pii*E*tan ( G )*tan ( G + Gt )*S )…
.dH = 20000*11,85662 / ( 2*Pii*E*tan ( 20 )*tan ( 20,57 )*1,68794 )…
.dH = 0,08 см.. .dH = 0,8 мм. С учетом того, что наружное кольцо и внутреннее
кольцо работают в паре и жесткость внутреннего примерно = наружного, то суммарная
осадка пары колец: .dH = 1,6 мм..
Реальный результат будет между результатами этих двух расчетов..
# ,,,,,,,,,,,,
Расcчитаем кольцевую пружину по формулам книги Р. С. Курендаш.
По расчетам приведенным выше:
Расчетное усилие принимаем Q = 20000 кгс.
Угол: Образующая – Ось кольца: G = 20º.. Высота расточки Lк = 12 мм.
Предполагаемый коэф. трения на конусе: Ктр = 0,1.. ( вибрация )..
Угол трения: Gt = arctan ( 0,1 )… Gt = 5,6666666º…
Наибольший диаметр расточки: Фк = ( Lк × 2 × ( tan 20º )) + Фв.. Фк = 112,7353 мм.
Площадь поперечного сечения кольца пружины: S = 1,68794 кв.см.
Объем кольца пружины: V = 62,8739 куб.см.. Масса = 0,49356 кг…
Средний диаметр кольца пружины: Фср = V / ( S × Pii )…
Фср = 62,8736 / ( 1,68794 × 3,1415926 ) .. Фср = 11,85662 см… Фср = 118,5662 мм.
Напряжение растяжения в сечении кольца:
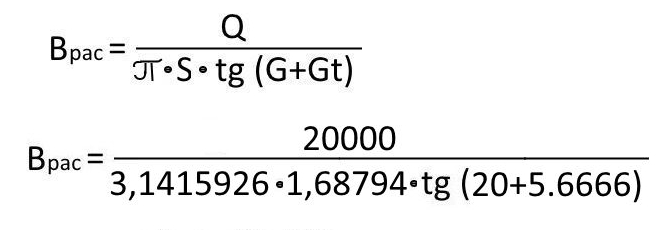
Врас = 7819,72 кгс/кв.см. Пружина вполне прочна..
Определим осадку жесткого конуса в упругое кольцо пружины:

.dH= 20000*( 11,85662/1,68794) / ( 3,1415926*2*tg(20+5,6666)*tg(20)*2000000 )…
.dH= 140486,27/ 2197937,7… .dH= 0,0639 см..
Поскольку на пружине внедряемый конус выполним с поперечным сечением равным поперечному сечению кольца, то конус сожмется на ту же величину на которую растягивается кольцо.
Поэтому реальное смещение вдоль оси удвоится и будет равно
2*dH = 0,128 см. на комплект Кольцо-Конус.
Проверим расчет исходя из найденной осадки конуса .dH = 0,639 мм..
( без учета сжатия конуса и без учета трения на конусе ).
Изменение радиуса при осадке .dR = .dH * tg 20.. .dR = 0,639 * 0,36397..
.dR = 0,2326 мм. Изменение диаметра .dd= 0,4652 мм.
Изменившийся средний диаметр Фсри = 118,5662+0,4652 = 119,031354 мм.
Изменившаяся длина окружности Ссри =119,031354 * Pii = 373,94803 мм.
Относительное изменение длины окружности Сотн = (Ссри–Ср) / Ср..
Сотн = (373,94803 –372,486703) / 372,486703.. Сотн = 1,461324 / 372,486703..
Сотн = 0,0039232… Далее по закону Гука..
При таком относительном удлинении напряжение растяжения будет:
Врас = Е * Сотн… Врас = 2000000 * 0,0039232… Врас =7846,3 кгс/кв.см.
Для пружинной стали напряжение нормальное..
Расчет напряжения растяжения по глубине внедрения конуса наиболее достоверен.
….. …..
График прогибов, в виду сложной картины деформации кольцевой пружины, рассчитать нереально –
– готовую пружину надо испытать на испытательном прессе со снятием характеристики
Анкерные шпильки предохраняются от обрыва гашением ударных нагрузок кольцевыми пружинами,
кроме того пружины равномерно распределяет нагрузку от станины между шпильками.
Кольцевая пружина хороша тем, что за счет трения на конических поверхностях
гасит колебания при ударных нагрузках при быстром затухании вибраций.
Пружина состоит из отдельных элементов, поэтому ее легко можно ремонтировать
заменив сломанный элемент.
Пружина достаточно проста в изготовлении.
На каждую шпильку с шагом резьбы t = 5 мм. желательно поставить по пять пар пружин
кольцо-конус.
При нагрузке 20000 кгс – пять пар пружин дадут осадку .dH = 8 мм.. По расчету приведенному выше
( без учета трения на конусе ). Для достижения нормальной нагрузки равной 11700 кгс.
Гайку шпильки надо затянуть на 4,8 мм ( доворот на 346 градусов ) после выборки зазоров, затем гайку законтрить по месту штифтом.
Анкерную шпильку обычно рвет в месте, где находится основание гайки.
Без применения пружин – обрыв расположен в верхней плоскости лапы стойки молота,
что осложняет или делает невозможным ремонт анкерной шпильки, методом приварки
нового резьбового наконечника шпильки взамен оторванного.
При применении кольцевых пружин – основание гайки будет поднято над верхней плоскостью лапы стойки- зона обрыва будет выше верхней плоскости лапы стойки.
Ремонт будет возможен.
Кстати все вышеизложенные расчеты эффективнее выполнять используя программы. Программы можно скопировать из книги « Python 3 Полезные программы книга третья ». Программы значительно экономят время и уменьшают вероятность ошибок в расчетах..
Расчет конусной муфты.
Расчет приведен для примера – он похож на расчет кольцевой пружины.
Проверим расчеты по формулам И.А. Биргера – ( по другой литературе ).
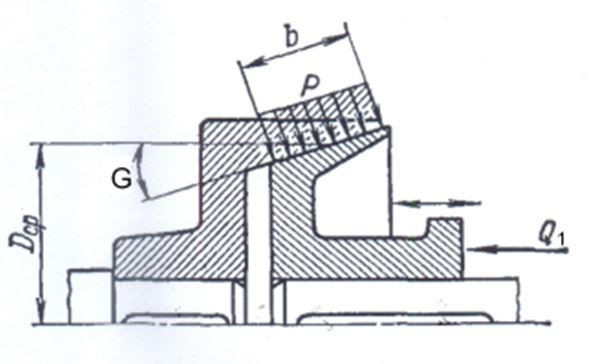
Определим давление на коническую поверхность обоймы при внедрении в обойму –
конуса с углом Ось – Образующая = 20º…
Усилие действующее к нормали конической поверхности: F…
Усилие загоняющее конус в коническую расточку: Q1…
Угол конической расточки: G… Угол трения: Gt ….
,,,
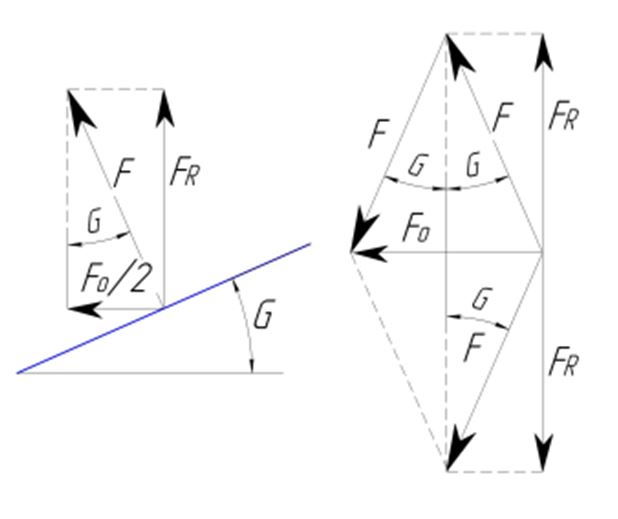
Осевое усилие: Q1 = F*2*( sin ( G )) …
Определяется усилие нормальное к конической поверхности:
F = 20000/(2*sin ( 20 )) … F = 29238 кгс… Трение не учитываем..
Так как в условиях вибрации, трение может значительно уменьшится.
Сила перпендикулярная оси обоймы муфты: FR = F*cos ( G )…
Зная усилие перпендикулярная оси обоймы и коэф. трения конуса об обойму находим
FR = 29238*0,9397 = 27475 кгс…
Fраз = FR = 27475 кгс… Это усилие приходится на два поперечных сечения обоймы.
Напряжение разрыва обоймы: Врк = Fраз /( 2*S )… Врк = 27475 /( 2*1,68794 )…
Врк = 8138,6 кгс / кв.см.…
Длина средней линии сечения: С = Фср*Pii… С = 11,857*Pii… С = 37,25 см…
По закону Гука длина средней линии увеличится при приложении силы ( напряжения ).
.dL = Врк *C / E… dL = 8138,6*37,25 / 2000000… dL = 0,1516 см… dL = 1,516 мм…
Соответственно диаметр станет больше на: dD = dL / Pii… dD = 1,516 / Pii ..
.dD = 0,4826 мм.. Радиус увеличится на: dR = 0,2413 мм.
Конус при этом зайдет глубже вдоль оси: Lос = dR / tan ( G ).. Lос = 0,2413 / 0,36397..
Lос = 0,663 мм… С учетом такой же деформации конуса – осадка = 1,326 мм
Вывод: При некотором несовпадении – результаты показывают возможность доверять расчету.
Расчет межцентрового ременной передачи.
Например при проектировании узла: Вентилятор – Приводной эл.двигатель – необходимо определить минимальное и максимальное межцентровое расстояние « А » учитывая допуск на изготовление клинового
ремня и его последующее вытягивание при эксплуатации и ГОСТовские размеры ремня.
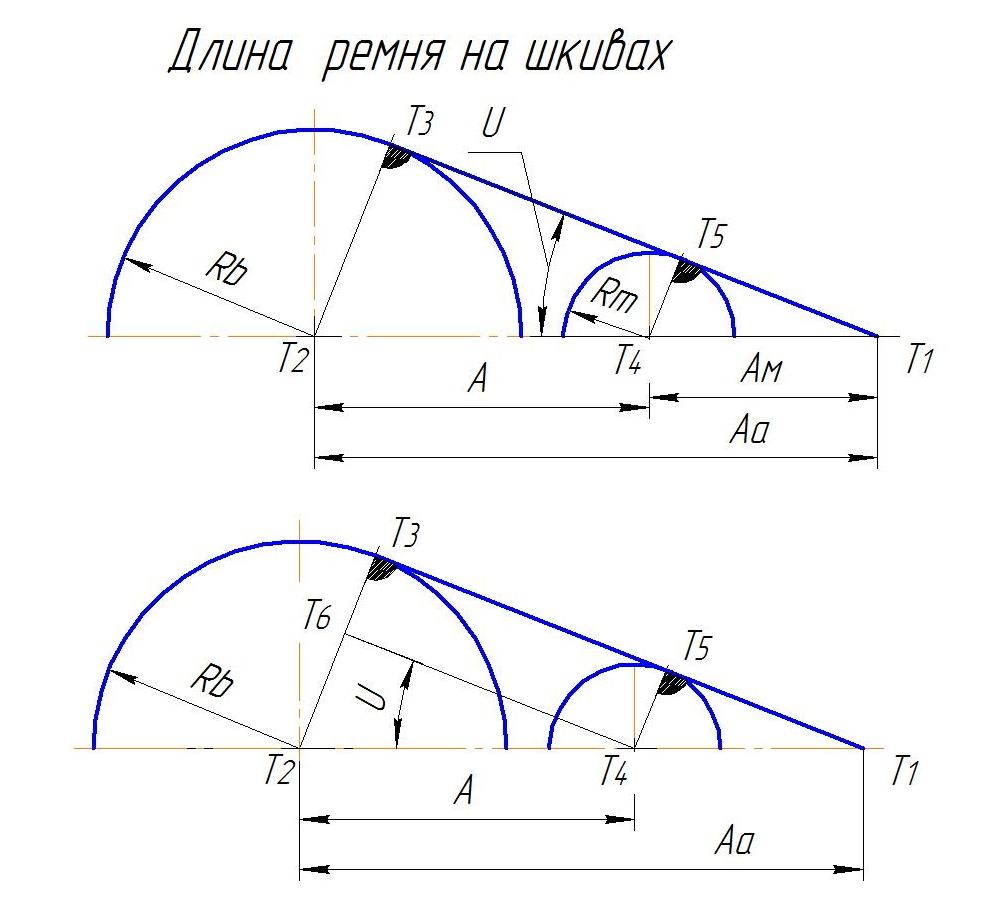
В расчет берется нейтральная линия ремня ( слой ремня который при изгибе не растягивается и не сжимается ).
Радиусы Rb и Rm – это радиусы нейтральной линии ремня ( расчетного диаметра dp ). Для клиновых ремней положение нейтральной линии определяется по таблицам. На приведенной таблице расчетный диаметр обозначен как dp.. Rb=dp/2…
Расчет рекомендуется выполнить по Программе выполненной на основе приведенного алгоритма расчета.
Принцип расчета:
Прямоугольные треугольники Т1-Т2-Т3; Т1- Т4–Т5 и Т4-Т2-Т6 подобные.
Линия Т1-Т3 параллельна линии Т4-Т6. Катет Т2-Т6 равен разности радиусов ( Rb-Rm )..
Находим угол U из условия ( Т2-Т6 ) = А * sin ( U ).. U = arcsin(( Т2-Т6 )/A )..
Зная угол U найдем угол G между прямыми Т2-Т3 и Т2-Т1..
Угол охвата ремнем малого шкива Uom = G+G …
Длина ремня на малом шкиве Lom = 2*Rm*Pii*Uom/360…
Угол охвата ремнем большого шкива Uob = 360-(G+G) …
Длина ремня на большом шкиве Lob = 2*Rb*Pii*Uob/360…
Длина ремня между точками касания ремнем шкивов Lp = A * cos( U )…
Полная длина ремня L = Lob+Lom+2*Lp…
Расчет не дает прямого решения. Задавая разные значения межцентрового А ..
Подбором находим длину ремня L… Смотрим – если длина не подходит по ГОСТ – пересчитываем снова.
Для ускорения подбора есть смысл написать программу на языке Бейсик, Python или на Pascal..
Многих отпугивает программирование – действительно профессиональное программирование требует большого объема знаний и постоянной тренировки. Однако для программирования вычислений и вывода на экран результата требуется не так уж много знаний, за то значительно облегчается расчетно- конструкторская работа.. Смотри книгу Python-3 Полезные программы книги книга первая, вторая, третья.. Гаврилов С.Ф…
Контрольный расчет:
Rb=500.. Rm=50.. A=570.. U=37,8622.. G=52,1378..
Lom =66,0845… Lob =2480,7474… Lp=349,8571… L=3246,5461…
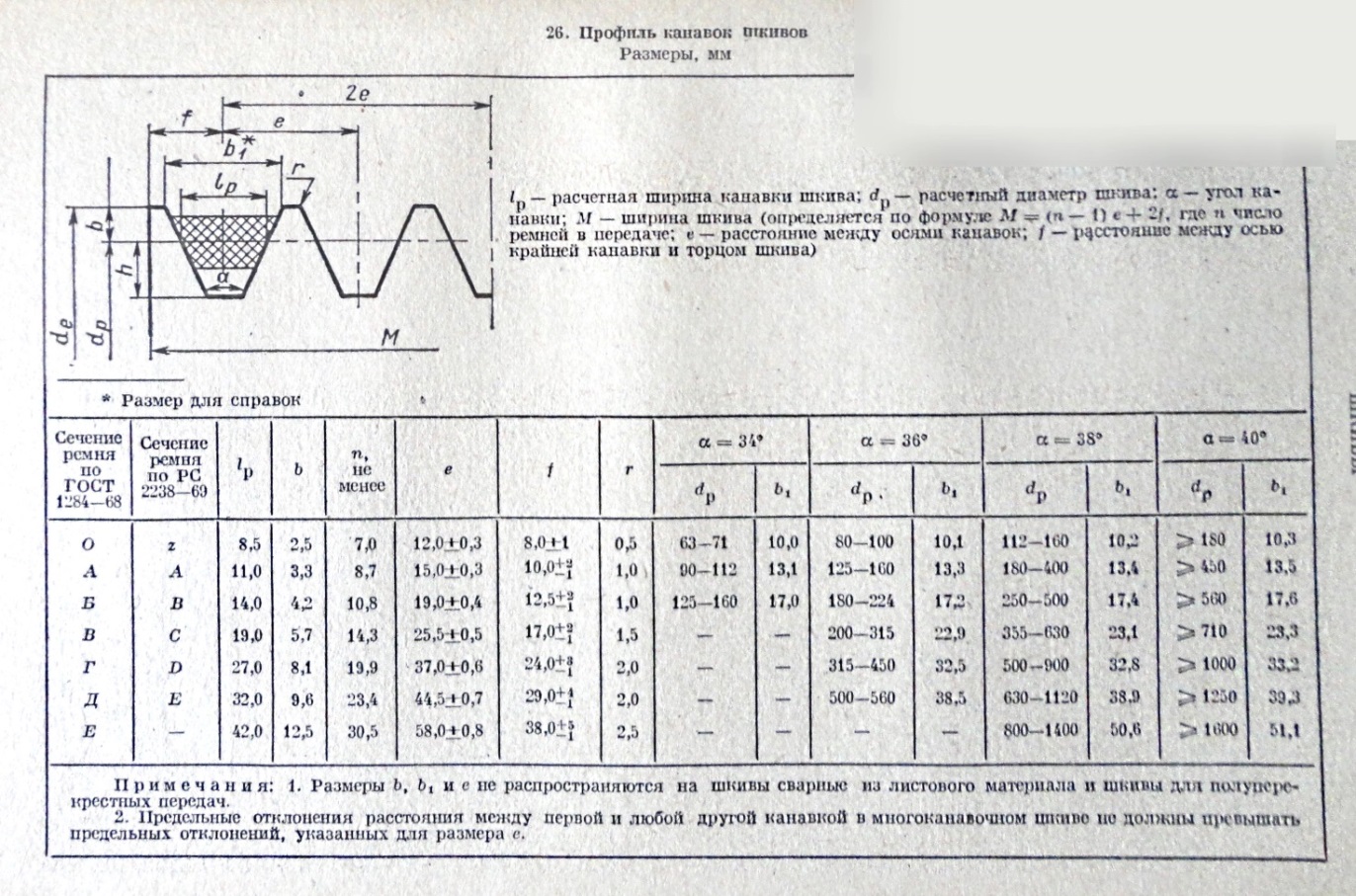
Таблица размеров сечения клиновых ремней.
Примечание: Обычно автор делает внутренний диаметр канавки под ремень на два-три мм. меньше чем
рекомендует таблица, при сохранении углов наклона – ремни при этом могут работать больший срок.
Таблица Rm-01.

Таблица размеров канавок для клиновых ремней. Таблица в книге получается неразборчивой.
Для устранения этого недостатка большие таблицы, рисунки и чертежи будут храниться на Яндекс диске, а в тексте книги будет приведено имя ( название ) и ссылка на файл.
Чтобы открыть файл по публичной ссылке, пользователям не обязательно иметь аккаунт на Диске.
Читатели по ссылке на Яндексе могут просмотреть файл или скачать его на свой компьютер.
Для этого Ссылку копируют в адресную ( самую верхнюю ) строку браузера – Ентер – и браузер откроет файл на которую вы получили ссылку..
## « Таблица размеров канавок клиновых ремней » Ссылка:
Ссылка Studenty.zip : https://disk.yandex.ru/d/orKSVHysYSMK0Q
Studenty.zip : CRC 32 = 77d05e10… Объем -= 77,916,434....
……..
Ссылка Студенту.zip : https://disk.yandex.ru/d/Rbo3M49TP3xMdg
Студенту.zip: CRC 32 = E76A2853… Объем -= 152458350…
…..
Таблица Rm-02.
Примечание: В таблице размер « b » показывает расположение нейтрального слоя ремня относительно наружного диаметра шкива..
## Для примера: Расчетная программа в Python-3 можно посмотреть по ссылке:
Передача Винт – Гайка.
Алгоритм расчета силового винта домкрата:
Исходные данные:
Поднимаемый груз Fg = 1000 кН.
Скорость подъема V = 0,003 м / сек.
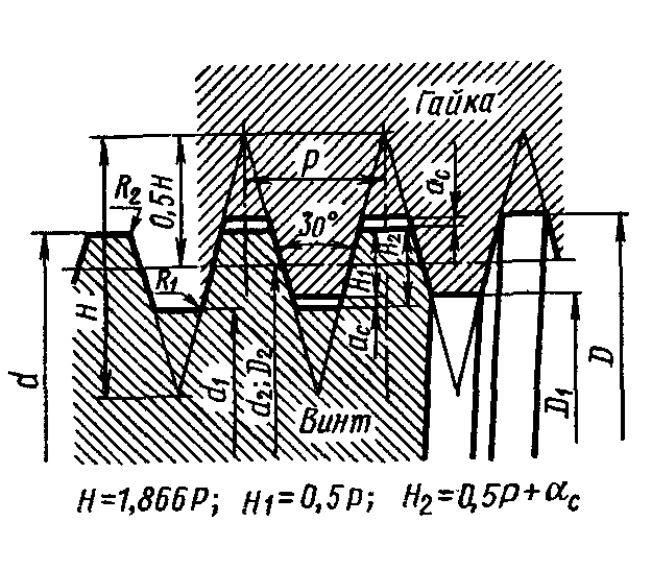
Винт с однозаходной трапецеидальной резьбой.
Число заходов резьбы: n = 1…
с шагом резьбы Р = 24 мм. Tr 120 × 24 ГОСТ 9484 – 81.
Наружный диаметр резьбы Dn = 120 мм.
Рабочая высота профиля Н1 = 0,5* Р; Н1 = 12 мм.
Угол между рабочей поверхностью
и нормалью к продольной оси винта Ua = 15 градусов..
Материал винта – сталь 40 Х ГОСТ 4543 –71.
Закалка с 860 градус.С в масло, отпуск с 400 град.С.
Класс 8.8 Временное сопротивление разрыву 800 Н/кв.мм. по ГОСТ 52643-2006..
Витки шлифованные.
Рабочая длина винта LL = 1000 мм.
Материал гайки оловянно свинцовая бронза БрО10С10 ГОСТ 613 – 79.
применяется на сильно нагруженных узлах скольжения.
Смазка скудная.
Кольцевой подпятник винта из закаленной стали 40 Х ГОСТ 4543 –71.
Опора подпятника:
По такой же закаленной шлифованной стали при скудной смазке.
Наружный диаметр подпятника: Dnp = 140 мм.
Внутренний диаметр подпятника: Dvp = 60 мм.
Расчет:
Мощность необходимая на подъем груза:
Ng = Fg * V; Ng = 1000000*0,003 = 3000 ватт.
Средний диаметр резьбы: Ds = Dn – 0,5*P; Ds = 120 – 12 = 108 мм.
Скорость вращения винта: Vu = V / ( P*n ); Vu = 0,003 / 0,024;
Vu = 0,125 об / сек… Vu = 7,5 об/мин.. Vu = 0,7854 рад/сек…
( w = 2*Pii*Vu… рад/сек. Vu в об/сек.. ).
Крутящий момент для подъема: Mpg=Ng/(2*Pii*Vu)…
Mpg=3000/(2*Pii*0,125)… Mpg=3819,72 Н*метр…
Линейная скорость витка винта относительно гайки: VL = Pii * Ds * Vu;
VL = Pii * 108 * 0,125 = 42.4115 мм / сек. VL = 0,0424115 м / сек..
Угол подъема средней винтовой линии резьбы:
Ur = arctan( P * n / ( Pii * Ds )); Ur = arctan( 24 / ( Pii * 108 ));
Ur = arctan ( 0,07073553 ); Ur = 4,04610810 градусов…
По таблице коэф. трения:
( сталь по бронзе при скудной смазке при скорости скольжения менее 1 м / сек.. ) коэф. трения КТf = 0,13…
Угол между рабочей поверхностью и нормалью к продольной оси винта Ua = 15 градусов..
Приведенный коэф. трения: КТfp = КТf / cos Ua; КТfp = 0,13 / cos(15); КТfp = 0,134586…
Сила трения: Ftrv= КТfp*Fg.. Ftrv= 0,134586*1000000.. Ftrv= 134586 H..
Момент трения на резьбе винта: MtR = Ds *Fg * КТfp / 2 ;
MtR = 0,108 * 1000000 * 0,134586 / 2; MtR = 7267,64 Н * метр.
Приведенный угол трения:
Up = arctan ( КТfp ); Up = arctan ( 0,134586 ); Up = 7,6651450…
Так как Up > Ur… ( Ur = 4,04610810 градусов ) … винтовая передача самотормозящая.
Мощность затрачиваемая на трение Винт – Гайка: Nvg = Ftrv * VL..
Nvg = 134586 * 0,0424115.. Nvg = 5708 вт…
Расчет подпятника винта:
Средний диаметр подпятника: Dsp = ( Dnp + Dvp ) / 2 ; Dsp = ( 140 + 60 ) / 2;
Dsp = 100 мм. Dsp = 0,1 метра.
Средняя скорость скольжения поверхности: Vp = Pii * Dsp * Vu;
Vp = Pii * 100 * 0,125; Vp = 39,26991 мм / сек. Vp = 0,03926991 м / сек.
По таблице коэф. трения: коэф. трения КТp = 0,3…
( сталь по стали при скудной смазке при скорости скольжения менее 1 м / сек.).
Момент трения на подпятнике: Mtp = Dsp *Fg * КТp / 2 ;
Mtp = 0,1 * 1000000 * 0,3 / 2; Mtp = 15000 Н * метр.
Мощность расходуемая на трение в подпятнике:
Np = Fg * КТp* Vp; Np =1000000*0,3*0,03926991; Np = 11,781 квт.
Мощность подводимая от привода к винту:
Nt = Ng + Np + NR; Nt = 3,0 +5,708+11,781 = 20,5 квт. Nt = 20,5 квт.
Крутящий момент подводимый к винту: Mk = Nt / ( Vu * 2 * Pii );
Mk = 20500 / ( 0,125 * 2 * Pii ); Mk = 26102 Н * метр…
Расчет винта на прочность:
Внутренний диаметр резьбы винта DVR = Dn -26; ( по ГОСТ 9484 – 81. )…
DVR = 120-26 = 94 мм.
Площадь поперечного сечения по внутреннему диаметру винта:
SVR = DVR * DVR * Pii / 4; SVR = 94 * 94 * Pii / 4 = 6939,778 кв.мм.
Максимальная допустимая нагрузка Fmdv=0,625*800*SVR… Fmdv=0,625*800*6939,778 …
Fmdv=3469890 H… Запас прочности К = 3469890/1000000… К=3,47… Винт прочен..
Расчет винта на устойчивость:
Момент инерции винта ( считаем по внутреннему диаметру резьбы ):
( 94 ** 4=78074896… Это 94 в четвертой степени )…
Jx = Pii * ( DVR ** 4 ) / 64; Jx = Pii * ( 94 ** 4 ) / 64;
Jx = Pii * 78074896 /64; Jx = 3832492,5 …
Площадь сечения ( считаем по внутреннему диаметру резьбы ):
SVR = 6939,778 кв.мм. ( рассчитано ранее )..
Радиус инерции сечения:
Ii = sqrt( Jx / SVR ); Ii = sqrt( 3832492,5 / 6939,778 ); Ii = 23,5 мм.
Винт внизу находится в достаточно длинной гайке – пологаем, что это жесткая заделка.
Сверху на винте свободно висит груз: При этой конструкции коэф. приведения длины винта Kп = 2…
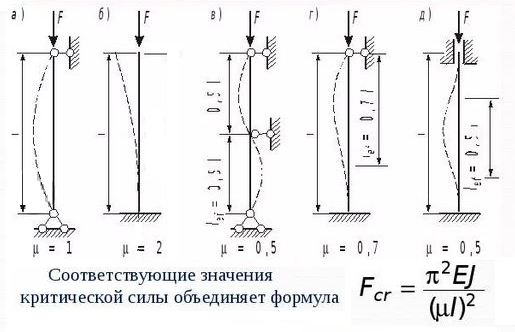
В нашем случае ( рис.b- мю = Кп = 2 )..
Гибкость винта: G = LL * Кп / Ii; G = 1000 * 2 / 23,5; G = 85,1…







