Петр Путенихин
Уравнения движения в расширяющейся Вселенной
5. Интегральный закон Хаббла
Несложно показать, что при использовании изменяющегося во времени параметра eH(t) мы получим интегральное уравнение движения а(t) или r(t).
Для этого все одинаковые интервалы времени записываем количественно, а не в порядковом виде. Каждое следующее состояние пространства является расширением предыдущего интервала, уже испытавшего соответствующее расширение.
Отмечаем, что все интервалы времени Δti равны друг другу, а Hi – это значение параметра Хаббла, соответствующее текущему моменту времени этого i-го интервала. Для визуализации будем в уравнениях предыдущий интервал отделять от следующего закрывающей скобкой. Чтобы избежать "размножения" сопутствующих им открывающих скобок, мы их просто опустим, помня, что их может быть столько же, сколько и закрывающих:

В первой строке показано, что расширение eHt испытал исходный интервал r0. Во второй строке расширение происходит теперь уже у этого уже расширившегося интервала в скобках. В третьей строке новым интервалом для расширения является итоговый интервал из второй строки. И так далее. Закономерность очевидна, она имеет вид:

Обнаруживаем, что сумма произведений мгновенного значения параметра Хаббла, соответствующего каждому краткому интервалу времени, выглядит как интеграл. Если длины интервалов устремить к нулю, то получим интеграл:

Верхним пределом интеграла является время T – сумма всех бесконечно малых интервалов времени dt просто потому, что количество слагаемых n как раз и равно количеству этих интервалов dt в общем времени: T = n×dt.
Выше такое же решение мы нашли для закона Хаббла с масштабным фактором (5) и (6). Уравнение описывает, как со временем увеличивается расстояние между двумя областями, находящимися в исходном состоянии на некотором расстоянии r0. Выше мы умышленно использовали константу в виде eH, чтобы получить именно такую запись (8), причем величина H окажется в точности равной постоянной Хаббла.
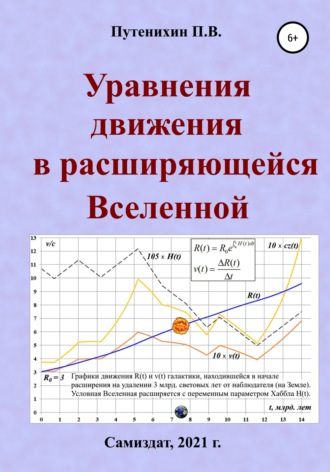
В заключение покажем, как с помощью этих уравнений производится построение диаграмм движения на примере условной галактики, сверхновой, находившейся в начале расширения пространства на удалении от Земли в 3 млрд. световых лет. Для наглядности рассмотрим условную Вселенную, расширяющуюся с параметром Хаббла H(t), имеющим множество изломов: участков убывания и возрастания.
На рис.1 этот переменный параметр Хаббла представлен графиком 105xH(t), где масштабный множитель 105 использован, чтобы график был хорошо различим, а его некруглое значение – чтобы он имел меньше пересечений с другими графиками. Интервал времени диаграмм равен 14 млрд. лет.
Используя уравнение (7), производим построение графика дистанций R(t). Построение производим по табличным данным, в которых текущее удаление рассчитывается как предыдущее, испытавшее шаговое расширение, расширение с текущим значением параметра Хаббла за единичный интервал времени.

Рис.1. Пример диаграмм движения для переменного H(t)
График скорости v(t) строим c 10-кратным масштабом простым вычислением прироста дистанции за интервал времени этого прироста. Шаг времени step выбран равным 0,1 млрд. лет. Для сравнения приведён также график скорости с 10-кратным масштабом, определяемой для больших значений красного смещения точным обратным уравнением, переводящим скорость в красное смещение:

Как видим, расхождение скоростей на рисунке существенное. Скорость, определяемая простым умножением красного смещения на скорость света получается почти в 2 раза больше реальной скорости объекта. Известно, что приблизительное равенство cz ≈ v выполняется только при малых значениях красного смещения, z < 0,1.

Рис.2. Диаграммы Хаббла для v(r) и cz(r) во Вселенной с параметром Хаббла H(r)
На рис.2 приведены традиционные диаграммы Хаббла для этого условного параметра Хаббла H(t). В вычислениях использовано интегральное значение параметра Хаббла (5).
Литература
1. Боджовальд М., В погоне за скачущей Вселенной, журнал "В мире науки", Космология, 2001, № 1, URL: http://www.chronos.msu.ru/old/RREPORTS/bodzhovald_pogonya.html
2. Инфляционная стадия расширения Вселенной, Элементы, URL: http://elementy.ru/trefil/21082
3. Космология ранней Вселенной, Соросовская Энциклопедия, 2005, URL:
http://www.astronet.ru/db/msg/1210276
4. Расширение пространства со сверхсветовой скоростью?, URL: https://otvet.mail.ru/question/62024653
5. Смолин Л., Атомы пространства и времени //ВМН, № 4, 2004
6. Теория стационарной Вселенной, Элементы, URL: