
К. В. Нестерова
Фискальная политика в многострановой модели общего экономического равновесия
© ФГБОУ ВО «Российская академия народного хозяйства и государственной службы при Президенте Российской Федерации», 2017
* * *
Введение
Данная модель работает для шести регионов/ стран. Непосредственной целью этой работы является построение и калибровка модели общего экономического равновесия с учетом России, в частности моделирование изменений фискальной политики.
Полученная модель позволит понять, как демографические изменения и фискальная политика во всем мире повлияют на рост реальной заработной платы, процентные ставки и экономический рост (как глобальный, так и региональный либо внутренний) с течением времени. Также в модели учитывается наделенность стран природными ресурсами – нефтью и газом. Это позволяет анализировать динамику развития стран с точки зрения объема их начального запаса, изменения его рыночной стоимости и его использования во времени – темпов извлечения ресурсов. Это особенно актуально для российской экономики.
В России наблюдается проблема старения населения, что в будущем создаст дополнительную нагрузку на пенсионную систему страны. Модель позволяет анализировать данные вопросы в рамках подхода общего равновесия в динамике. Это дает возможность учесть взаимозависимость различных мер, таких как изменение в будущем пенсионного возраста, налогов и цен на энергоносители. Модель различает различные виды налогов, и с ее помощью можно сравнивать эффект от изменения различных ставок: например, можно проанализировать общие потери от повышения налога на потребление или налога на заработную плату, а также распределение данных потерь по поколениям.
Настоящая модель позволяет также оценивать долгосрочный эффект налоговой политики в открытой экономике, а также распределение этого эффекта между поколениями, что является актуальным фактором при принятии политических решений.
Тема настоящего исследования представляется весьма актуальной в связи с разработкой мер, направленных на стабилизацию экономики после негативного шока нефтяных цен в конце 2014 г., а также реализацией плана антикризисных мер и мер, направленных на устойчивое долгосрочное развитие экономики[1].
1. Построение расчетной модели общего экономического равновесия для США, Европы, Японии, Китая, Индии и России
Демографические процессы моделируются как полностью экзогенные, т. е. рождаемость и смертность изначально задаются чисто внешним образом и не зависят от эндогенной динамики модели. При том что возрастная структура играет ключевую роль в данной модели, половая структура нами игнорируется, поэтому агенты не имеют половой принадлежности. В каждый период времени агент с некоторой вероятностью может стать родителем вне зависимости от количества детей, которых агент уже имеет к этому моменту. В каждом регионе продолжительность жизни агентов не превосходит 90 лет, поэтому количество поколений, проживающих одновременно в каждый момент времени, равно 91. Весь период жизни репрезентативного агента разбивается на несколько стадий, имеющих существенные отличия. Первая стадия начинается с момента рождения и заканчивается, когда он достигает возраста 20 лет. На первой стадии агент не предлагает рабочую силу на рынке труда, не имеет активов и поддерживается своим родителем. В возрасте 21 года агент выходит на рынок труда и получает возможность держать активы и лишается поддержки родителя. Следующая стадия начинается в возрасте 23 лет и заканчивается, когда агент достигает 45 лет. В данный период агенты могут иметь детей, причем, как было указано выше, вероятность, с которой рождаются дети, является внешним параметром.
Для упрощения аналитических выкладок количество детей, которое может иметь агент в каждый год, считается не дискретным, а непрерывным и одинаковым для всего поколения данного возраста в рамках одного региона. Такое предположение позволяет сохранить свойство репрезентативности и избежать гетерогенности структуры популяции, когда агенты, принадлежащие к одному поколению, отличаются по количеству детей и, следовательно, имеют разные условия принятия решений. Иначе говоря, в каждый период времени все агенты одинакового возраста рождают некоторое одинаковое (в общем случае нецелое) число детей, а общее число детей, которое имеет тот или иной агент в заданном периоде времени, представлено суммой соответствующих чисел за все предыдущие годы детородного возраста. Такой подход позволяет достаточно точно воспроизвести демографические процессы, сохраняя гомогенность агентов в рамках каждого отдельного поколения. Данный подход был описан в работе [6].
Детородная стадия заканчивается, когда агент находится в возрасте 45 лет, и до 66 лет он продолжает поддерживать всех рожденных детей. При таком моделировании, когда агент достигает возраста 66 лет, самые позднее поколение детей (т. е. поколение, которое он родил в возрасте 45 лет) достигает второй стадии, когда они становятся самостоятельными. Следовательно, после 66 лет агент уже не участвует в поддержке детей, поскольку они получают доступ к рынку труда и могут обеспечивать себя автономно. С 68 лет начинается последняя стадия жизни, когда агент с некоторой экзогенно заданной вероятностью может умереть. Максимальная продолжительность жизни равна 90 годам, поэтому последняя стадия для самого долгоживущего агента длится с 68 до 90 лет. При такой постановке дети не умирают раньше своего родителя, что имеет значение для моделирования процесса наследования, т. е. передачи активов от родителя детям после его смерти.
После смерти агента активы, которыми он располагал, перераспределяются в качестве наследства среди части популяции агентов по определенному правилу. Подобное перераспределение используется для упрощения, поскольку позволяет сохранить репрезентативную структуру популяции. Если предположить, что после смерти родителя наследство перераспределяется только среди его детей, то в рамках одного поколения будут агенты как с живым, так и с уже умершим родителем, т. е. агенты, принадлежащие к одному поколению, будут отличаться, поскольку последние получат к тому моменту наследство.
Модель не предполагает, что родитель получает полезность от того, что оставляет наследство детям, поэтому в последней стадии жизни агенты держат активы, только чтобы финансировать собственное потребление и не создают специальных сбережений, чтобы передать их детям.
Миграция в модели также предполагается экзогенной. В каждом периоде популяция увеличивается за счет мигрировавших агентов, при этом возрастная структура, а также класс производительности мигрантов зависят от региона. Для сохранения гомогенности популяции делается предположение, в соответствии с которым распределение всех характеристик в группе прибывающих в некотором периоде мигрантов совпадает с соответствующим распределением этих характеристик во всей популяции. Все вероятностные распределения, определяющие динамику рождения детей и смертность, переносятся с основной популяции на мигрантов.
Предпочтения домохозяйств отражаются приведенной ниже сепарабельной функцией полезности, которая предполагает как компоненту, связанную с собственным потреблением и досугом, так и компоненту, соответствующую потреблению детей, которых поддерживает агент. Общая полезность агента выражается функцией U(a, t, k), где t является индексом времени, a обозначает возраст агента в годах, а k соответствует классу производительности, к которому принадлежит агент. Компоненту полезности от собственного потребления и досуга обозначим через V(a, t, k), а полезность от потребления всех детей данного агента обозначим через H(a, t, k). Таким образом,

Спецификация для функции собственной полезности следующая:

Уровень потребления агента, относящегося к когорте возраста а и принадлежащего к классу продуктивности к, в периоде t обозначен через с(а, t, к). Время, которое данный агент тратит на досуг, обозначено через l(а, t, к), а е является специальным параметром полезности от индивидуального досуга. Однопериодная функция полезности агента является CES-функцией от потребления и времени индивидуального досуга, а соответствующий параметр внутривременной эластичности замещения обозначен через р. Вероятность, с которой агент, чей возраст в периоде t равен а, доживет до периода i, обозначена через Р(а, i, t). Смертность в модели не зависит от класса продуктивности агента. Параметры δ и γ характеризуют межвременные предпочтения домохозяйств.
Общая собственная полезность агента, таким образом, равна сумме взвешенных CES-агрегаторов будущего потребления и досуга, а взвешивающими множителями выступают вероятности дожития и факторы временных предпочтений.
Полезность, которую агент получает от уровня потребления его детей, имеет вид, сходный с видом функции собственной полезности. Так в полезность родителя входит дисконтированная сумма полезности от будущего потребления всех его детей, включая тех, чье рождение ожидается в будущем. Вид соответствующей функции следующий:

В периоде t рассмотрим агента, который относится к когорте возраста a и классу производительности k. Число детей, которые у него будут, когда агент достигнет возраста i, обозначим через KID(a, i, t, k), а потребление каждого ребенка – через cK(a, i, t, k).
Если ввести дополнительное обозначение d(a, z, t) для вероятности, с которой агент заданного поколения умрет в возрасте равном ровно z, то вероятность дожития P(a, i, t) можно представить в виде:

Совокупная стоимость активов, которыми в периоде t располагает агент, относящийся к классу производительности k и принадлежащий поколению возраста a, обозначим через A(a, t, k). В каждом периоде агент получает доход от предложения труда, платит налоги и получает трансферты, получает наследство от родителя и затрачивает средства на собственное потребление и потребление своих детей. В соответствии с предположениями модели, в каждый период времени у агента есть общий запас времени, который он может распределить между досугом, входящим в его функцию полезности, и рабочим временем. Общий запас доступного времени обозначим как h(a, t), тогда время, которое агент будет предлагать на рынке труда, равно h(a, t) – l(a, t, k). Обозначив зарплату, выплачиваемую за единицу рабочего времени, через w(t, k), можно получить выражение для трудового дохода агента в виде:
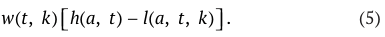
Общие затраты на потребление (собственное и потребление детей) представляются в виде:
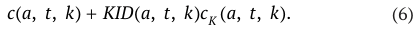
Наследство, полученное агентом, обозначим как I(a, t, k). Чистую стоимость уплачиваемых агентом налогов обозначим через T(a, t, k). Тогда, если обозначить ставку доходности как r(t), уравнение, описывающее динамику стоимости активов, принадлежащей выбранному агенту, можно записать следующим образом:

Активы, находившиеся в собственности всех умерших агентов в рамках одного класса производительности, суммируются в общий пул и затем распределяются среди живущих агентов этого класса в возрасте от 23 до 67 лет. Если общая стоимость пула активов равна A(t, k), то вся когорта агентов в возрасте l получает долю Г(l, t) этого пула и эти активы равномерно распределяются среди членов когорты, численность которой обозначена как N(l, t, k). Соответственно, данные доли суммируются к единице по всем указанным возрастам:

При этом распределение Г(l, t) соответствует распределению по возрастам всех детей агентов, умерших в данном году. Правило, в соответствии с которым агент из когорты возраста l получает долю наследства, задается формулой:
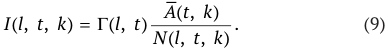
Технический прогресс задается через повышение эффективности труда со временем. Этот эффект моделируется нами следующим образом. Предполагается, что общий запас времени, которое агент может распределять между досугом и трудом, увеличивается с одинаковым ежегодным темпом λ. Это может быть интерпретировано как то, что постепенно с течением времени рабочая сила становится более продуктивной (см. [6]). С учетом введенного ранее обозначения h(a, i) для общего запаса времени, которым располагает агент возраста a в периоде i, технический прогресс задается правилом:

Такой метод моделирования технического прогресса обеспечивает сходимость к долгосрочному устойчивому равновесию. Иные способы моделирования технического прогресса, включая добавления специальных множителей, отвечающих за рост производительности труда в производственную функцию, создают трудности для корректного определения долгосрочного равновесия при заданной структуре предпочтений. Это, в свою очередь, создает проблемы при использовании итерационного метода определения траектории, по которой экономика сходится к своему долгосрочному равновесию. Причина этого в том, что для использования данного метода ключевую роль играют терминальные условия, т. е. условия, соответствующие долгосрочному равновесию экономики.
Трудовой доход, получаемый агентом класса производительности k в периоде i, складывается как произведение индивидуального предложения труда (рабочего времени) на размер повременной заработной платы. Последнее представляет собой произведение зарплаты w(k, i), зависящей от периода времени и класса производительности работника, на коэффициент производительности E(a, i), который также зависит от периода времени и возраста работника.



