Познавательные психические процессы: Хрестоматия

Полная версия

Г. В. Гершуни, Е. Н. Соколов
Объективное измерение чувствительности и субсенсорная ее область^[4]

В психологических исследованиях чувствительность человека характеризуют чаще всего порогом ощущения, т. е. порогом осознания факта воздействия внешнего раздражителя и речевого сообщения об этом. Однако давно известно, что далеко не все из того, что воспринимается человеком и афферентирует его поведение, осознается. Например, еще в 1863 году сотрудница И. М. Сеченова Н. Суслова наблюдала в эксперименте эффект неосознаваемого восприятия. Она заметила, что характер ощущений, вызванных штриховым прикосновением к коже волоском Фрея или ножками циркуля Вебера, изменяется при прохождении через кожу слабого электрического тока, который сам по себе не вызывает каких-либо ощущений. Еще в прошлом веке стали известны факты бинаурального взаимодействия: изменение локализации источника звука, слышимого одним ухом, под влиянием другого, неслышимого звука, подаваемого на второе ухо (Урбанчич, 1881).

Существование зоны чувствительности человека к неощущаемым раздражениям было прямо доказано в опытах известного советского физиолога Г. В. Гершуни. Позднее эта зона была определена им и количественно.

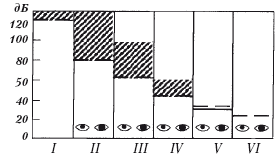
Рис. 1.2. Взаимоотношение порогов улитко-зрачкового рефлекса и порогов слухового ощущения на разных стадиях течения патологического процесса у больных с нарушением слуха после воздушной контузии. Ордината – интенсивность звукового раздражения в децибелах относительно нормального абсолютного слухового порога (0 дБ); абсцисса – стадии патологического процесса. 130 дБ – полная глухота; сплошная жирная линия – порог слухового ощущения; пунктирная – порог улитко-зрачкового рефлекса; заштрихованная поверхность – диапазон субсенсорной активности. I – тотчас после травмы; II–V – стадия восстановления слуховой чувствительности; VI – норма. Внизу – схематическое изображение степени расширения зрачка (слева при отсутствии раздражения, справа – при действии звука)

Во время Второй мировой войны Г. В. Гершуни обследовал больных с закрытыми травмами головного мозга после воздушной контузии, страдавших «постконтузионной глухотой» (Гершуни, 1947). Он обнаружил, что сразу после контузии, когда слуховые ощущения либо полностью отсутствуют, либо появляются только при действии очень сильных звуков, возникают такие ответные реакции организма, как изменение спонтанной электрической активности коры головного мозга – появление ритмов более высоких частот, чем до звука, изменение разности потенциалов кожи (кожно-гальваническая реакция) и улиткозрачковый рефлекс – изменение диаметра зрачка при действии звука. При нормальном слухе улитко-зрачковый рефлекс возникает при действии звуков, интенсивность которых превышает порог слухового ощущения на 25–30 дБ. В условиях же патологии этот рефлекс возникает при интенсивности звука на 20–60 дБ ниже порога ощущения и улитко-зрачкового рефлекса по мере восстановления слуховой функции (см. рис. 1.2). Сначала улитко-зрачковый рефлекс заметно усиливается, порог его резко снижается (II–III стадии патологического процесса). Это происходит потому, что мозговые структуры, ответственные за появление улитко-зрачкового рефлекса (не только средний мозг, где находится эффекторное ядро рефлекса, но и его представительство в коре), раньше выходят из тормозного состояния, чем отделы коры, определяющие возникновение ощущения. В результате этого снижения порога улитко-зрачкового рефлекса существенно возрастает зона неслышимых звуков, которые вызывают этот рефлекс. Эта зона была названа Гершуни субсенсорной областью.

В дальнейшем происходит снижение порога не только улитко-зрачкового рефлекса, но и порога ощущения, субсенсорная область уменьшается (стадии III, IV) и, наконец, отношения между слуховыми ощущением и улитко-зрачковой реакцией нормализуются – слух восстановлен (стадии V, VI).

<…> Описанная динамика непроизвольных реакций человека при снижении чувствительности в результате патологического процесса использовалась в дальнейшем для диагностики и прогноза восстановления чувствительности.

Более поздние исследования Г. В. Гершуни и его сотрудников показали, что субсенсорная область существует и в норме. Ее пределы сильно зависят от функционального состояния человека и колеблются от 5 до 12 дБ для слуха. <…>

<…> В ряде случаев объективные реакции представляют единственную возможность измерения чувствительности: у маленьких детей, еще не полностью овладевших речью, при патологии головного мозга, связанной с нарушением речевой функции, при симуляции нечувствительности, а также во всех тех случаях, когда желательно провести измерение чувствительности, не привлекая внимания испытуемого к раздражителям специальной инструкцией, обусловливающей ответную реакцию.

Какие реакции организма используются в качестве объективных индикаторов чувствительности?

Целый ряд реакций, не поддающихся прямому произвольному контролю и возникающих при действии раздражителя как в самой сенсорной системе, так и в других системах организма рефлекторным путем. Перечислим их:

– реакции рецепторов (микрофонный эффект улитки, электроретинограмма и т. д.). Применение этих реакций в качестве индикаторов чувствительности весьма ограниченно, так как они позволяют судить только о состоянии периферического отдела анализатора;

– реакции корковых отделов анализаторов (вызванные потенциалы, изменение спонтанной электрической активности коры, например депрессия хорошо выраженного альфа-ритма (8–2 к/сек);

– различные компоненты ориентировочного рефлекса (сужение кровеносных сосудов конечностей, кожно-гальванический рефлекс, движение глаз и головы в направлении раздражителя и др.);

– специальные адаптационные рефлексы (сужение зрачка на свет, сужение периферических кровеносных сосудов на холод);

– безусловно-рефлекторные реакции (например, рассмотреный выше улитко-зрачковый рефлекс). Все перечисленные выше реакции возникают «с места», без предварительной выработки;

– различные условно-рефлекторные реакции, вырабатываемые в результате сочетания условного агента с различными специальными раздражителями. Обычно в качестве условного агента используется раздражитель, адекватный для того анализатора, чувствительность которого измеряется. Выбор же подкрепления зависит от характера вырабатываемой условно-рефлекторной реакции: для депрессии альфа-ритма – свет, для кожно-гальванической реакции – электрокожное раздражение, для мигания – вдувание воздуха в глаз. Определение чувствительности с помощью непроизвольных реакций ведется общепринятыми психофизическими методами, обычно методом постоянных раздражений.

В. Гершуни и Е. Н. Соколовым (Гершуни, 1957; Соколов, 1958) были проведены многочисленные исследования соотношения порогов различных реакций, вызванных одним и тем же раздражителем, определены ограничения и возможности использования отдельных реакций в качестве индикаторов чувствительности. Основные результаты этих исследований схематически представлены на рис. 1.3. Эта схема показывает ряд характерных соотношений разных реакций в процессе измерения чувствительности. Чувствительность к индифферентным раздражителям может быть измерена только с помощью непроизвольных реакций типа R₃ и оказывается довольно низкой (стадия I). Когда же раздражителю придается сигнальное значение, чувствительность возрастает, пороги разных реакций расходятся. Наиболее низкий порог имеют непроизвольные реакции, являющиеся компонентами ориентировочного рефлекса. Пороги ощущений, о которых мы судим по речевым ответам (R₁, реч.), устанавливаются постепенно по мере уточнения смысла инструкции экспериментальной ситуацией и достигают своего высшего уровня.

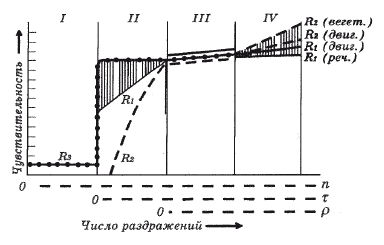
Рис. 1.3. Схема изменений, определяемая по разным реакциям чувствительного анализатора в зависимости от общего числа наносимых раздражителей n, раздражителей, являющихся сигналами определенных ответных реакций, r и числа неподкрепляемых (дифференцировочных) раздражителей p. R₁ – реакции, обусловленные речевой инструкцией испытуемому: R₁ реч. – словесный ответ (типа «Вижу», «Слышу».); R₁ двиг. – произвольная условная двигательная реакция. R₂ – условно-рефлекторные реакции, вырабатываемые при безусловном подкреплении: R₂ двиг. – условные мигательные; R₂ вегет. – условные кожно-гальванические. R₃ – реакции, возникающие без специальной выработки и речевых инструкций. Область расхождения порогов непроизвольных и словесной реакции заштрихована. I–IV – стадии изменения чувствительности. Переход от I стадии ко II соответствует приобретению раздражителем значения условного сигнала реакции R₁ или R₂. Ось ординат – чувствительность в условных единицах; ось абсцисс – число n, r, p

На следующей, третьей стадии происходит упрочение и дифференцирование выработанных условных рефлексов. В силу этого ориентировочные реакции сохранны. Пороги всех реакций практически совпадают. Когда условные реакции упрочены (IV стадия), непроизвольные ориентировочные реакции угасают. Если о чувствительности анализатора судить только по ним, может показаться, что она резко снизилась. Однако пороги ощущения (R₁, реч.) остаются на прежнем уровне, пороги произвольных условных двигательных реакций (R₁, двиг.) даже несколько снижаются, т. е. при автоматизации обусловленного инструкцией ответного движения, например нажатия рукой на кнопку, иногда появляются неосознаваемые двигательные ответы на неощущаемые раздражители. Все другие реакции показывают более высокую чувствительность анализатора, и пороги условно-рефлекторных непроизвольных реакций оказываются несколько ниже порогов ощущения и произвольного двигательного ответа. Эта разница характеризует величину субсенсорной чувствительности нормального здорового человека.

На основании этих данных исследователи приходят к выводу о необходимости, во-первых, разделения понятий порога реакции и порога анализатора в целом и, во-вторых, о необходимости полиэффекторной регистрации ряда произвольных и непроизвольных реакций человека в процессе измерения чувствительности. Это позволяет получить полную и точную характеристику предельных сенсорных возможностей, с одной стороны, и обоснованное суждение о чувствительности анализатора, которая в каждый данный момент зависит от условий, характера и задачи деятельности, выполняемой человеком, – с другой.

П. О. Макаров
Об основном психофизическом законе^[5]

Два столетия назад, в 1760 г., Бугер исследовал свою способность различать тень, отбрасываемую свечой, если экран, на который падает тень, одновременно освещается другой свечой. Его измерения довольно точно установили, что отношение DI/I (DI – минимальный воспринимаемый прирост освещения, I — исходное освещение) – величина сравнительно постоянная, в отличие от абсолютных величин. В 1834 г. Вебер повторил забытые к тому времени опыты Бугера. Изучая различение веса, он показал, что минимально воспринимаемая разница в весе представляет собой постоянную величину, равную приблизительно ¹/₃₀, т. е. груз в 31 г различается от груза в 30 г; груз в 62 г от груза в 60 г; 124 г от 120 г и т. д. Такое же постоянство в отношении минимального воспринимаемого прироста раздражения к его исходной величине Вебер установил для зрения (различение длины линий) и слуха (различение высоты тона). Вебер предполагал, что им обнаружен важный общий принцип, однако специального закона он не сформулировал.

Выражение «закон Вебера» принадлежит Фехнеру, но впоследствии укоренилось выражение «закон Вебера – Фехнера», так как роль Фехнера в разработке проблемы измерения ощущений исключительно велика. Фехнер рассуждал следующим образом. Мы не можем измерить ощущение. Мы можем только удостоверить, если одно ощущение больше, меньше или равно другому ощущению. Но поскольку мы можем измерять стимулы, мы можем измерить и минимальный стимул, необходимый для вызова ощущения или для того, чтобы минимально усилить или минимально ослабить имеющееся в наличии ощущение. Поступая таким образом, мы измеряем чувствительность как величину, обратную порогу. Фехнер ввел понятие об абсолютной и различительной (или дифференциальной, или разностной) чувствительности: абсолютная чувствительность измеряется абсолютным порогом, т. е. минимальной интенсивностью раздражения, вызывающей ощущение, различительная чувствительность измеряется разностным порогом, т. е. минимальным ростом интенсивности раздражения, вызывающим усиление или ослабление ощущения, по отношению к исходной интенсивности раздражения. Так, если груз в 60 г (R) оценивается как равный по весу в 61 г и чуть более легкий, чем груз в 62 г (R₁), минимальный воспринимаемый прирост веса будет равен:

ΔR =R_i −R = 62 − 60 = 2r,

а разностный порог (отношение Вебера) будет равен

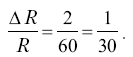
Закон Вебера выражается, таким образом, формулой

ΔR/R = константа (1)

для едва воспринимаемого прироста величины раздражения R.

Фехнер предположил, что если ΔR/R = константа, то и минимальный прирост ощущения (ΔS) относительно исходного уровня ощущения (S) тоже константа, т. е.

ΔS = c(ΔR/R), (2)

где с – константа пропорциональности. Формула (2) – это «основная формула Фехнера». Введение ΔS в уравнение (2) следует рассматривать как заключение Фехнера о равенстве между собой всех ΔS, всех минимальных приростов ощущения. Таким образом, приросты ощущения ΔS рассматриваются Фехнером как единицы измерения. Интегрируя уравнение (2), Фехнер получил

S = c log_eR + C, (3)

где С – константа интегрирования, а е – основание натуральных логарифмов. С помощью этой формулы, зная обе константы с и С, можно вычислить величину ощущения для стимула любой интенсивности. Однако поскольку константы неизвестны, эта формула неудовлетворительна, и Фехнер заменил С, сделав допущение о нулевой величине S при пороговой величине R. При R = r, т. е. при величине раздражения, равной абсолютному порогу, S = 0.

Подставляя значения R и S при R = r в формулу (3), получаем

0 = c log_er + C,

C = – c log_e r.

Теперь мы можем заменить С в формуле (3):

S = c log_e R – c log_e r = c (log_e R – log_e r) = c log_e (R/r).

Путем соответствующего изменения константы c на k переходят от натуральных логарифмов к десятичным, тогда

S=k lg (R/r). (4)

Это и есть Massformel Фехнера – формула для измерения ощущений. Шкала S – это шкала едва различимых приростов ощущения над нулем, т. е. над ощущением при абсолютном пороге. Затем Фехнер сделал еще одно допущение. Он предположил, что мы можем измерять R, любой надпороговый стимул, его отношением к r, пороговому стимулу. Если, таким образом, принять r за единицу измерения, r = 1, то

S = k Ig R. (5)

Этой последней формуле (5) Фехнер и дал название «закон Вебера». Выраженная словами, она гласит: величина ощущения пропорциональна логарифму величины раздражения. Разумеется, закон Вебера выражается формулой (1), а не формулой (5). Формула (5) выведена, как мы видели, при ряде условных допущений: во-первых, что единицей R является пороговая величина стимула г, во-вторых, что S = 0 при пороге, т. е. при R = г, в-третьих, что все ΔS, все минимальные воспринимаемые приросты величины раздражения, равны между собой. Прежде всего формула (5) требует соблюдения формулы (1), а между тем последующие эксперименты показали, что отношение Вебера постоянно не во всем диапазоне интенсивностей раздражения. Тем не менее, несмотря на бесчисленную критику и все ограничения, закон Бугера – Вебера – Фехнера имеет достаточно широкую зону приложения. Существенно, что формула Фехнера (5) приложима к деятельности некоторых изолированных рецепторов. В определенном диапазоне интенсивностей частота токов действия есть линейная функция логарифма интенсивности. Это показано на мышечном веретене Мэтьюсом (1931) и на глазу Limulus Хартлайном и Грэмом (1932). Разумеется, здесь приходится говорить не об S-ощущении, а об E-возбуждении:

E = k lg R.

Фехнер соединял в себе физика, психофизиолога и философа-идеалиста. Отвергая его идеалистические построения, мы должны признать, что, как физик, он внес в физиологию органов чувств человека новые точнейшие методы количественного измерения отношения стимул – ответ. Это, во-первых, уже описанный нами метод измерения едва различимых приростов величины раздражения, позже названный методом пределов, во-вторых, метод проб и ошибок, позже названный методом постоянного стимула (исследуемый сравнивает целый ряд стимулов с одним и тем же постоянным стимулом по какому-нибудь признаку – больше или меньше, темнее или светлее, длиннее или короче и т. д.), и в-третьих, метод средней ошибки (исследуемый сам подбирает стимул, равный заданному или в то или иное число раз больший или меньший заданного). Фехнер установил значение изменчивости при «психофизических», как он выражался, измерениях, необходимость определения средних и крайних величин и законы изменчивости средних величин, т. е. установил необходимость статистических методов.

Фехнер считается одним из основателей экспериментальной психологии, а физиологи вправе сказать, что он развил открытие Бугера – Вебера в закон, разработал метод измерения различительной чувствительности органов чувств и, таким образом, заложил основы измерения нервных процессов у человека. <…>

С. С. Стивенс
Психофизика сенсорной функции^[6]

<…> С самого начала необходимо признать, что психофизике зачастую не удавалось выполнить стоящую перед ней задачу на должном уровне. Ее задача не из легких. Прежде всего всякий раз, когда выдвигались предположения о возможности подвергнуть ощущение упорядоченному количественному исследованию, старые предрассудки, унаследованные в основном от дуалистической метафизики, порождали целый ряд упорных возражений. Вы не можете, говорили критики, измерить внутреннюю, индивидуальную, субъективную силу того или иного ощущения. Может быть, это и так, говорим мы, в том смысле, в каком это понимают те, кто нам возражает. Однако в другом и весьма полезном смысле сила ощущения может быть, как мы увидим далее, с успехом определена количественно. Нам нужно оставить в стороне споры о внутренней жизни разума. Мы должны задать себе разумные объективные вопросы об отношениях между входом и выходом сенсорных преобразователей, учитывая при этом то, как эти отношения раскрываются в поведении организмов, будь то животные или люди. Другая трудность состоит в том, что у психофизики было несчастливое детство. Хотя еще в пятидесятых годах XIX века Плато сделал нерешительную попытку правильно определить форму функции путем соотнесения воспринимаемой интенсивности с интенсивностью раздражителя, тем не менее его голос был заглушен Фехнером, который сковал развитие только что зародившейся дисциплины, обременив ее глубоко ошибочным «законом», носящим его имя (Стивенс, 1957). Быть может, самой трудной задачей, стоящей перед нами, является освобождение науки от господства столетней догмы, утверждающей, что интенсивность ощущения возрастает как логарифм интенсивности раздражителя (закон Фехнера). На самом деле данное отношение вовсе не выражается логарифмической функцией. К настоящему времени на примере более чем двадцати сенсорных континуумов показано, что кажущаяся или субъективная величина возрастает как степенная функция от интенсивности раздражителя и что показатели степенной функции лежат в пределах от 0,33 для яркости до 3,5 для электрического раздражения (60 герц) для пальцев руки. Иными словами, по-видимому, существует простой и повсеместно действующий психофизический закон – закон, о котором одно время догадывался Плато и от которого он впоследствии отказался <…>.

<… > Выводя свой логарифмический закон, Фехнер ошибочно предполагал, что минимальный прирост ощущения (ΔS) будто бы есть постоянная величина на всем протяжении психологической шкалы. Хотя он хотел предположить, что постоянным является отношение едва заметного изменения раздражителя (ΔR)² к его исходной величине (R), т. е.

ΔR/R = k (закон Вебера),

у него получилось, что постоянно ΔS. Из этих двух предположений он вывел отношение:

S = k log R

и тем самым нанес большой вред всему делу.

<… > Предположим, что Фехнер принял бы положение о постоянстве отношения не только для е. з. р. стимуляции ΔR, также и для субъективного коррелята е. з. р. – ΔS. Тогда он смог бы написать:

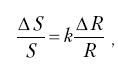
откуда следовало бы, что психическая величина S является степенной функцией физической величины R. Однако он отбросил это предположение, когда оно впервые было сделано Брентано. В результате временной победы Фехнера в психофизике открылся период бесплодных исследований, когда казалось, что нет более интересной работы, чем измерение е. з. р. Так логарифмический закон стал «пещерным идолом».

<….> Начиная с 30-х годов XX века значение психофизики стало восстанавливаться. Новый интерес к очень старой проблеме сенсорного ответа возник благодаря изобретению методов, описывающих соотношение входа и выхода сенсорных систем. Эти методы показывают, что сенсорные ответы возрастают по степенному закону. При изучении поведения так редко удается показать, что простое отношение сохраняется при самых различных видах стимуляции, что широкое распространение и постоянство степенного закона действительно приобретают большое значение.

Конечно, можно себе представить, что ощущения всех модальностей возрастают одинаково с увеличением интенсивности стимуляции. На самом деле это совсем не так, и это легко доказать при помощи элементарного сравнения. Заметьте, что, например, происходит при удвоении освещенности пятна света и, с другой стороны, силы тока (частота 60 Гц), пропускаемого через палец. Удвоение освещенности пятна на темном фоне удивительно мало влияет на его видимую яркость. По оценке типичного наблюдателя, кажущееся увеличение составляет всего лишь 25 %. При удвоении же силы тока ощущение удара увеличивается в десять раз.

<… > Степенная функция имеет то преимущество, что при использовании логарифмического масштаба на обеих осях она выражается прямой линией, наклон которой соответствует значению показателя. Это видно на рис. 1.4: медленное увеличение яркостного контраста и быстрое усиление ощущения удара электрическим током. Для сравнения на этом рисунке показана также функция оценки видимой длины линий, сделанной несколькими наблюдателями. Здесь, как и следовало ожидать, показатель функции лишь немного отличается от 1,0. Иначе говоря, для большинства людей отрезок 100 см кажется вдвое длиннее, чем отрезок 50 см.

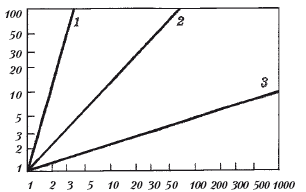
Рис 1.4. Зависимости субъективной величины (ощущения) от величины раздражителя для трех модальностей, представленные в логарифмическом масштабе на обеих осях. 1. Электрический удар. 2. Кажущаяся длина. 3. Яркость. Абсцисса – величина раздражения (условные единицы); ордината – психологическая величина (произвольные единицы)

На рис. 1.5 те же самые три функции представлены в линейных координатах.

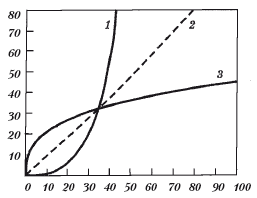
Рис. 1.5. Те же зависимости, что и на предыдущем рисунке, представленные в линейных координатах. Форма функции, вогнутая или выпуклая, зависит от величины показателя степени: n больше или меньше 1,0. Обозначения кривых и осей те же, что и на предыдущем рисунке

<…> В своей практике автор еще ни разу не встретил исключения из этого закона (отсюда и смелость называть эту зависимость законом).

В табл. 1.1 указаны показатели степенных функций некоторых из исследованных континуумов.