
Edgars Auziņš
Ātrā matemātika verbālās skaitīšanas noslēpumi
3. nodaļa Skaitļu reizināšana virs un zem atsauces numura
Līdz šim mēs esam reizinājuši skaitļus, kas ir vai nu virs vai zem atsauces skaitļa. Kā reizināt skaitļus, no kuriem viens atrodas virs atsauces, bet otrs zemāk?
Apskatīsim, kā rīkoties, kā piemēru izmantojot produktu 96 x 135. Mēs izmantosim 100 kā atsauces numuru:

98 ir mazāks par atsauces skaitli 100, tāpēc zem tā novelkam apli. Cik mazāk? Ar 2 tas nozīmē, ka aplī ierakstām skaitli 2. 135 ir lielāks par 100, tāpēc mēs novelkam apli virs 135. Cik vēl? Tāpēc pie 35 mēs aplī ievadām 35.
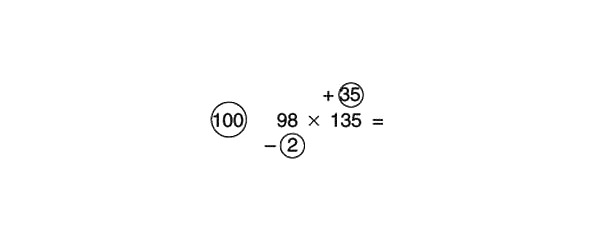
135 ir vienāds ar 100 plus 35, tāpēc mēs ievietojam plus zīmi 35 priekšā. 98 ir 100 mīnus 2, kas nozīmē, ka mums ir jāievieto mīnus zīme pirms 2 aplī.
Tagad mēs aprēķinām šķērsām. Mēs ņemam vai nu 98 plus 35, vai 135 mīnus 2. 135 mīnus 2 ir vienāds ar 133. Aiz vienādības zīmes ierakstiet 133. Tagad sareizināsim 133 ar atsauces skaitli 100. 133 ar 100 ir vienāds ar 13300. (Lai reizinātu jebkuru skaitli ar 100, vienkārši pievienojiet divas nulles pa labi no tā.) Piemēra risinājums tagad izskatās šādi:
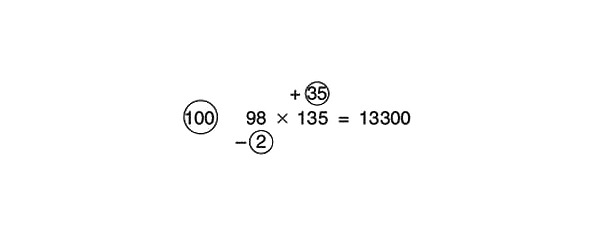
Tagad reizināsim skaitļus apļos. 2 ar 35 dod 70. Tiesa, tā nav pilnīgi taisnība. Faktiski mums ir jāreizina 35 un mīnus 2. Atbilde attiecīgi būs mīnus 70. Tagad piemēra risinājums izskatās šādi:
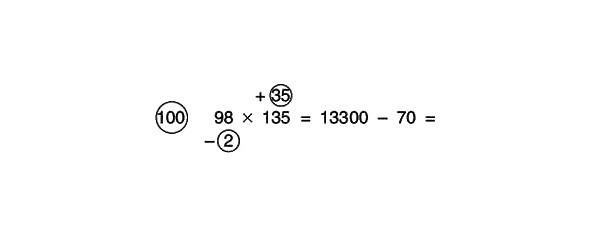
Ātrās atņemšanas metode
Paņemsim pauzi no piemēra risināšanas uz brīdi un redzēsim, kāds ir īsākais veids, kā atrast divu skaitļu starpību. Kāds ir vienkāršākais veids, kā no skaitļa atņemt 70? Ļaujiet man uzdot jautājumu citā veidā: kāds ir vienkāršākais veids, kā garīgi atņemt 9 no 56?
56 – 9 =
Esmu pārliecināts, ka jūs zināt pareizo atbildi, bet kā jūs to ieguvāt? Daži cilvēki vispirms atņem 6 no 56, lai iegūtu 50, un pēc tam no 9 atņem atlikušo 3, lai iegūtu 47.
Daži cilvēki atņemtu 10 no 56 un iegūtu 46. Tad viņi pievienoja 1 atbildei, jo liekais tika noņemts (10 = 9 +1). Rezultāts atkal būtu 47.
Kāds cits šo problēmu atrisinātu ar kolonnu uz papīra. Tajā pašā laikā viņam prātā būtu jāpārnes un jāieņem kategorijas. Tas, iespējams, ir garākais risinājums. Neaizmirstiet, ka:
Vienkāršākais veids, kā atrisināt problēmu, ir ātrākais un kļūdīgākais.
Lielākajai daļai cilvēku vienkāršākais veids, kā no skaitļa atņemt 9, ir vispirms atņemt 10 un pēc tam pievienot 1. Vienkāršākais veids, kā atņemt 8, ir atņemt 10 un pēc tam pievienot 2. Lai atņemtu 7, atņem 10 un pēc tam pievieno 3. atbilde. Šeit ir vēl daži «vienkāršāki» veidi:
• Kāds ir vienkāršākais veids, kā no skaitļa atņemt 90? Atņemiet no tā 100 un pievienojiet 10.
• Kāds ir vienkāršākais veids, kā no skaitļa atņemt 80? Atņemiet no tā 100 un pievienojiet 20.
• Kāds ir vienkāršākais veids, kā no skaitļa atņemt 70? Atņemiet no tā 100 un pievienojiet 30.
Atgriežoties pie mūsu piemēra, kā no 13 300 atņemt 70? Vispirms atņemiet 100 un pēc tam pievienojiet 30. Vienkārši, vai ne? Pamēģināsim vēlreiz. 13300 mīnus 100. 13200. Plus 30. 13230. Šādi izskatās pilnībā atrisinātais piemērs:
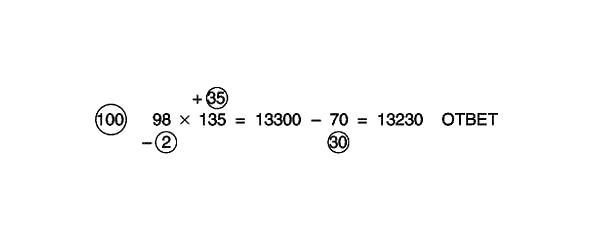
Nedaudz praktizējot, jūs varēsiet atrisināt līdzīgus piemērus savā galvā. Izmēģiniet tālāk norādītos piemērus.
a) 98 x 145 = ___; b) 97 x 125 = ___; c) 95 x 120 = ___; d) 96 x 125 = ___; e) 98 x 146 = ___;
e) 9 x 15 = ___; g) 8 x 12 = ___; 3) 7 x 12 = ___
Atbildes:
a) 14210; b) 12125; c) 11400; d) 12000; e) 14308; f) 135; g) 96; h) 84
Skaitļu reizinājums apļos
Noteikums, saskaņā ar kuru tiek atrasts skaitļu reizinājums apļos, ir:
Ja abi apļi atrodas virs vai zem faktoriem, tad to reizinājumu pievienojam starprezultātam. Kad viens no apļiem atrodas virs faktoriem, bet otrs zem tiem, no starprezultāta atņemam apļos esošo skaitļu reizinājumu.
Matemātiskā izteiksmē, reizinot divus pozitīvus (plus) skaitļus, atbildē iegūstam pozitīvu (plus) skaitli. Reizinot divus negatīvus (mīnus) skaitļus, mēs iegūstam arī pozitīvu (plus) skaitli. Reizinot pozitīvu (plus) skaitli ar negatīvu (mīnusu), mēs iegūstam negatīvu (mīnus) skaitli.
Vai mūsu metode ir piemērojama produktam 8 x 45?
Mēģināsim pārbaudīt. Ņemsim par atsauci skaitli 10. 8 ir par 2 mazāks par 10, bet 45 ir par 35 vairāk.
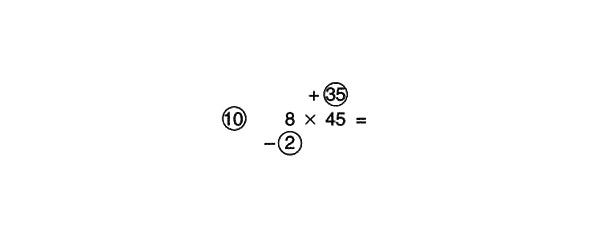
No 45 atņem 2 vai pievieno 35 līdz 8. No 45 mīnus 2 iegūst 43; reizinot ar atsauces skaitli 10, iegūstam 430. Mīnus 2, reizinot ar 35, iegūst 70. Lai no 430 atņemtu 70, vispirms atņemiet 100, kas iegūst 330, un pievienojiet 30, iegūstot 360.
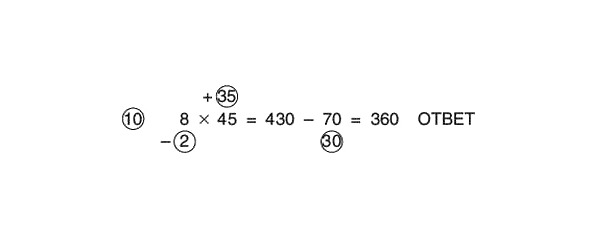
Vai tas nozīmē, ka jums vispār nav jāapgūst reizināšanas tabula? Nē, es tikai ierosinu citu veidu, kā to atcerēties. Kad esat nostrādājis desmit vai vairāk reizes, ka 7 pār 8 ir vienāds ar 56 un 13 virs 14 ir vienāds ar 182, jums tas vairs nebūs jādara: atbilde paliks jūsu atmiņā. Tas ir daudz produktīvāks veids nekā vienkārša pieblīvēšana.
Mēs joprojām neesam pabeiguši ar reizināšanu, bet paņemsim pārtraukumu un pavadīsim laiku, lai nostiprinātu to, ko esam iemācījušies līdz šim. Ja dažu uzdevumu risināšana jums joprojām ir sarežģīta, neuztraucieties: mums ir vēl daudz piemēru.
Nākamajā nodaļā mēs apskatīsim vienkāršu metodi saņemto atbilžu pārbaudei.
4. nodaļa Atbilžu pārbaude: pirmā daļa
Vai vēlaties pareizi atrisināt katru uzdevumu jebkurā skolas pārbaudījumā? Vai vēlaties iegūt tādas personas reputāciju, kas nekad nekļūdās aprēķinos? Ja tā, es iemācīšu jums pamanīt un izlabot kļūdu, pirms kāds pamanīs jūsu kļūdu.
Es saviem skolēniem bieži saku, ka matemātikā nepietiek ar atbildes izdomāšanu; problēma nav atrisināta, kamēr neesat pārbaudījis saņemto atbildi.
Es neizstrādāju atbilžu pārbaudes metodi, ko grasos jums piedāvāt. Matemātiķi par to ir zinājuši, iespējams, tūkstoš gadus, bet fakts ir tāds, ka vairumā valstu tas nez kāpēc nebija iekļauts skolu programmā.
Bērnībā es ļoti daudz kļūdījos aprēķinos tīri aiz neuzmanības. Es zināju, kā risināt problēmas un darīju visu pareizi. Bet atbilde joprojām izrādījās nepareiza. Es vai nu aizmirsu pārnest pakāpi, vai arī neuzmanības dēļ pierakstīju nepareizus skaitļus, un Dievs zina, kādēļ es pieļāvu kaitinošas kļūdas.
Skolotāji un vecāki man pastāvīgi atgādināja, ka man vienmēr ir jāpārbauda savi lēmumi. Bet vienīgais veids, kā es zinu, kā to izdarīt, ir vēlreiz atrisināt problēmu. Tomēr, ja atbilde bija atšķirīga, kā es varu zināt, kurā gadījumā tā ir pareiza? Varbūt es pirmo reizi problēmu atrisināju pareizi, bet, risinot vēlreiz, kļūdījos? Tāpēc mums problēma bija jāatrisina trešo reizi. Ja divas no trim atbildēm saskanēja, tad, kā es argumentēju, šī, iespējams, bija pareizā atbilde. Ko darīt, ja es vienkārši pieļautu vienu un to pašu kļūdu divas reizes? Man ieteica problēmu atrisināt divos dažādos veidos. Šis bija labs padoms. Tomēr testos nevienam netiek dots laiks vienu un to pašu problēmu atrisināt trīs reizes. Ja kāds tajā laikā man būtu iemācījis to, ko es jums mācīšu, es droši vien būtu pazīstams kā matemātikas ģēnijs.
Mani kaitina, ka šī metode tolaik bija zināma, bet neviens man to neiemācīja. To sauc par skaitļa ciparu saskaitīšanu vai devītnieku izmešanu. Tālāk ir norādīts, kā tas darbojas.
Aizvietošanas numuri
Lai pārbaudītu, vai atbilde ir pareiza, mēs izmantojam aizstāšanas skaitļus, nevis tos, kas izmantoti piemērā. Futbola vai basketbola komandas aizstājēji spēlē spēlētāju aizstāšanai. Līdzīgi darīsim ar cipariem, piemeklējot tiem piemērotus «rezerves». Pēdējais palīdzēs mums pārbaudīt, vai esam nonākuši pie pareizās atbildes ar galvenajiem uzdevuma skaitļiem.
Apskatīsim to ar piemēru. Pieņemsim, ka jūs tikko sareizinājāt ar 13 un 14 un ieguvāt 182. Jums jāpārbauda, vai šī ir pareizā atbilde.
13 x 14 = 182
Vispirms mums ir skaitlis 13. Atradīsim tā ciparu summu un iegūstam pirmo aizstāšanu:
1 +3 = 4
4 kļūst par aizstājējzīmi 13.
Nākamais skaitlis ir 14. Atradīsim arī tam aizstājēju, kuram saskaitām tā skaitļus:
1 +4 = 5
5 kalpo kā 14 aizstāšana.
Tagad veiksim reizināšanu, izmantojot aizstājējus, nevis sākotnējos skaitļus:
4 x 5 = 20
20 atkal ir divciparu skaitlis, tāpēc pievienosim tā ciparus un iegūsim mūsu kontrolnumuru, kas palīdzēs noteikt atbildes pareizību:
2 +0 = 2
2 ir kontroles skaitlis, ko izmanto, lai noteiktu atbildes pareizību.
Ja oriģinālo piemēru atrisinājām pareizi, tad atbildes ciparu summai jāsakrīt ar kontrolskaitli.
Mēs saskaitām saņemtās sākotnējās atbildes skaitļus:
1 +8 +2 = 11
11 ir divciparu skaitlis, bet mums ir nepieciešams viencipara skaitlis, tāpēc pievienosim tā ciparus:
1 +1 = 2
2 ir arī aizstāšanas numurs, bet šoreiz tiek pārbaudīta atbilde. Tā kā tas sakrita ar čeka numuru, piemērs tika atrisināts pareizi.
Mēģināsim vēlreiz, ņemot produktu 13 x 15:
13 x 15 = 195
1 +3 = 4 (aizstāt 13)
1 +5 = 6 (aizstāt 15)
4 x 6 = 24
24 ir divciparu skaitlis; Lai iegūtu nepārprotamu skaitli, saskaitīsim tā skaitļus:
2 +4 = 6
6 ir mūsu kontroles numurs.
Tagad, lai pārbaudītu, vai piemēru atrisinājām pareizi, saskaitīsim saņemtās sākotnējās atbildes skaitļus.
1 +9 +5 = 15
Pārvērsīsim 15 par viencipara skaitli:
1 +5 = 6
Tā kā šī atbilde sakrīt ar kontroles numuru, mēs varam būt pārliecināti, ka mēs neesam kļūdījušies, risinot sākotnējo piemēru.
Deviņnieku izmešana
Ir metode, kas ļauj vēl vairāk samazināt šīs procedūras laiku. Ikreiz, kad pārbaudes laikā savos aprēķinos sastopam skaitli 9, varam to droši izsvītrot. Iepriekš saņemtās atbildes gadījumā – 195 – tā vietā, lai atrastu summu 1 +9 +5, mēs varētu vienkārši izsvītrot 9 un pievienot tikai 1 +5, kas kopā iegūtu 6. Tas neietekmē rezultātu. jebkādā veidā, bet tas ļauj izvairīties no lieka darba un ietaupīt laiku. Man vienmēr patīk šādas lietas.
Kā ir ar atbildi uz pirmo atrisināto piemēru – 182?
Mēs pievienojām 1 +2 +8, lai iegūtu 11, un pēc tam pievienojām 1 +1, lai iegūtu kontrolskaitli 2. 182. gadā divi cipari tiek summēti 9: 1 un 8. Vienkārši izsvītrojiet tos, un rezultāts ir nepieciešamais skaitlis 2. Un jums nekas nav jādara.
Atrisināsim vēl vienu piemēru, lai redzētu, kā šī metode darbojas:
167 x 346 = 57782
1 +6 +7 = 14
1 +4 = 5
Ar pirmo numuru nebija nekādas viltības. 5 ir 167 aizstāšana.
3 +4 +6 =
Mēs uzreiz pamanām, ka 3 +6 = 9, tāpēc mēs izsvītrojam 3 un 6 tā, it kā tie nekad nebūtu bijuši. Atliek 4, kas ir skaitļa 346 aizstāšana.
Vai mūsu pārbaudāmajā atbildes piemērā ir deviņi vai skaitļi, kas kopā veido 9? Jā, ir: 7 +2 = 9, tāpēc mēs šos skaitļus izsvītrojam. Mēs saskaitām pārējos: 5 +7 +8 = 20. Tad 2 +0 = 2. Šis ir skaitlis, kas kalpo kā atbildes aizstāšana.
Parasti aizstāšanas skaitļus rakstu ar zīmuli virs vai zem piemēra faktoriem. Tas varētu izskatīties šādi:
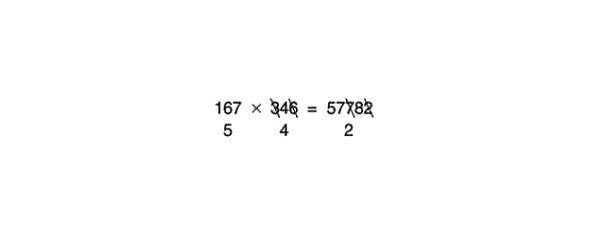
Tātad, vai saņemtā atbilde bija pareiza?
Reizinām aizvietošanas skaitļus: 5 ar 4 iegūst 20. Skaitlī 20 esošo ciparu summa ir 2 (2 +0 = 2). Mēs saņēmām skaitli, kas vienāds ar kontroles numuru, tāpēc atbilde ir pareiza.
Apskatīsim citu piemēru:
456 x 831 = 368936
Rakstīsim aizstāšanas skaitļus zem faktoriem:

Tas nebija grūti, jo no pirmā reizinātāja izsvītrojām 4 un 5, un mums palika 6; tad no otrā faktora izsvītrojām 8 un 1, atstājot mums 3; un tad atbildē izdevās izsvītrot gandrīz visus ciparus.
Tagad redzēsim, ko mums dod aizstāšanas skaitļi. 6 reiz 3 ir vienāds ar 18, kuru cipari kopā ir 9, kurus var arī izsvītrot. Tas atstāj 0. Mūsu kontroles skaitlis ir 8. Tas nozīmē, ka mēs kaut kur pieļāvām kļūdu.
Atkārtoti atrisinot piemēru, mēs iegūstam 378936.
Vai šoreiz saņēmām pareizo atbildi? 936 var izsvītrot, pēc tam saskaitām pirmos trīs ciparus: 3 +7 +8 = 18, kas saskaita 9, kas arī atstāj 0, tāpēc to var izmest. Ir sakritība ar kontrolnumuru, kas nozīmē, ka šoreiz atbilde saņemta pareizi.
Vai devītnieku izmešanas metode pierāda, ka mums ir pareizā atbilde? Nē, bet mēs varam būt gandrīz droši, ka atbilde ir pareiza (skat. 16. nodaļu). Piemēram, pieņemsim, ka pēdējā piemēra atbildē mēs saņēmām 3789360, tā beigās kļūdaini pievienojot papildu nulli. Tas neatspoguļosies čekā, metot devītniekus, un mēs nevarēsim noteikt, vai ir pieļauta kļūda. Tomēr gadījumos, kad metodes izmantošana norāda uz kļūdu, mēs varam būt pilnīgi pārliecināti, ka tā ir.
Deviņnieku ripināšana ir vienkāršs un ātrs tests, kas ļauj viegli pamanīt kļūdas. Varat būt pārliecināts, ka metode palīdzēs atrisināt matemātikas pārbaudes darbus bez kļūdām.
Kā šī metode darbojas?
Padomājiet par skaitli un reiziniet to ar 9. Cik ir 4 reiz 9? 36. Saskaitīsim šī skaitļa ciparus (3 +6), un rezultāts būs 9.
Mēģināsim ar citu numuru. 3 reizes 9 ir vienāds ar 27. Saskaitiet skaitļus (2 +7) un atkal iegūstam 9.
11 reizes 9 ir 99. 9 plus 9 ir 18. Nepareiza atbilde? Ne tik ātri. 18 ir divciparu skaitlis, tāpēc saskaitīsim skaitļus vēlreiz: 1 +8. Atkal atbilde ir 9.
Ja jebkuru skaitli reizinat ar 9, iegūtā skaitļa summa vienmēr būs 9, ja turpināsiet pievienot ciparus, līdz iegūstat viencipara skaitli. Tas ir vienkāršs veids, kā noskaidrot, vai skaitlis dalās ar 9 bez atlikuma.
Ja skaitļa cipariem saskaita 9 vai tā daudzkārtni, tad pats skaitlis bez atlikuma dalās ar 9. Tieši tāpēc, ja jebkuru skaitli reizina ar 9 vai tā daudzkārtni, skaitļa cipari kas iegūts reizināšanas rezultātā, jāsaskaita 9 (līdz iegūstat viencipara skaitli). Piemēram, jums ir jāpārbauda, vai tālāk norādītais piemērs ir pareizi atrisināts:
135 x 83615 = 11288025
Saskaitīsim pirmā faktora skaitļus:
1 +3 +5 = 9
Lai pārbaudītu atbildi, mums nav jāpievieno otrā faktora (83615) cipari, jo mēs zinām, ka skaitļa 135 ciparu summa ir 9. Ja atbilde ir pareiza, arī tā cipariem ir jāsaskaita. līdz 9.
Atradīsim atbildes ciparu summu:
1 +1 +2 +8 +8 +0 +2 +5 =
Divreiz var izsvītrot 8 +1, atstājot 2 +2 +5, kas dod 9. Tātad, pārbaude parādīja, ka atbilde ir pareiza.
Var atklāt arī citas interesantas lietas.
Ja skaitļa cipariem tiek pievienots cits skaitlis, nevis 9, tad tas ir atlikums, ko iegūstat, dalot sākotnējo skaitli ar 9.
Ņemsim, piemēram, 14. 1 plus 4 dod 5. Tātad 5 ir skaitļu 14 summa. Tas ir atlikums, ko iegūstat, ja dalāt 14 ar 9. Pārbaudīsim: 14 tiek dalīts ar 9 vienreiz, un atlikums ir 14–9, kas veido 5. Ja skaitlim pievienojat 3, tad, dalot šo skaitli ar 9, atlikumam pievieno 3. Ja skaitli dubultojat, atlikums atkal dubultojas. Citiem vārdiem sakot, neatkarīgi no tā, ko jūs darāt ar skaitli, jūs to darāt ar atlikumu, dalītu ar 9, tāpēc šie atlikumi var kalpot kā aizstāšanas skaitļi.
Kāpēc mēs izmantojam atlikumus, dalītus ar 9? Vai nav iespējams izmantot atlikumus no dalīšanas, piemēram, ar 17? Protams, jūs varat, bet dalīt ar 17 ir tik sarežģīts, ka pārbaudīt, vai jūsu atbilde ir pareiza, galu galā būs grūtāk nekā pats uzdevums. Mēs izvēlamies skaitli 9, jo ir vienkāršs veids, kā noteikt atlikumu, dalot ar to.
Vairāk par to, kāpēc šī metode darbojas, uzzināsiet E pielikumā.
5. nodaļa Reizināšana: otrā daļa
1. nodaļā mēs uzzinājām, kā reizināt skaitļus, izmantojot vienkāršu metodi, kas padara to par vieglu. To ir viegli izmantot, ja faktori ir skaitļi, kas ir aptuveni 10 vai 100. Kā ir ar skaitļu reizināšanu ar 30 vai 60? Vai ir iespējams izmantot mūsu pētīto metodi arī viņiem? Neapšaubāmi.
Mēs izvēlējāmies 10 un 100 kā atsauces skaitļus, jo tos ir viegli reizināt. Metode lieliski darbosies ar citiem atsauces numuriem, taču jums vajadzētu mēģināt izvēlēties tos, ar kuriem ir viegli reizināt.
Reizināšana ar faktoriem
To ir viegli reizināt ar 20, jo 20 ir vienāds ar 2 x 10, ko ir ļoti viegli reizināt ar. Mēs runājam par reizināšanu ar koeficientiem, un 10 un 2 ir skaitļa 20 koeficienti.
10 x 2 = 20
Apskatīsim piemēru:
23 x 24 =
23 un 24 ir lielāki par atsauces skaitli 20, tāpēc pār faktoriem apvelkam apļus. Vairāk, bet par cik? Attiecīgi 3 un 4. Mēs ievadām šos skaitļus atbilstošajos apļos, kurus mēs uzzīmējām augšpusē, jo mēs runājam par pozitīviem skaitļiem (23 = 20 +3, 24 = 20 +4).
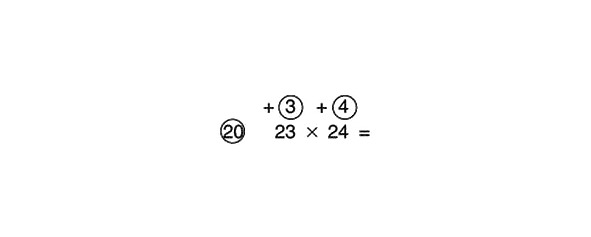
Salieciet to šķērsām, kā iepriekš:
23 +4 = 27 vai 24 +3 = 27
Tagad sareizināsim saņemto atbildi ar atsauces numuru 20. Lai to izdarītu, vispirms reiziniet ar 2 un pēc tam ar 10:
27 x 2 = 54
54 x 10 = 540
(Vēlāk šajā nodaļā apskatīsim vienkāršu veidu, kā reizināt 27 ar 2.) Citādi viss ir vienāds. Mēs reizinām skaitļus apļos un starprezultātam pievienojam 540.
3 x 4 = 12
540 +12 = 552
Pilnībā atrisināts piemērs izskatās šādi:
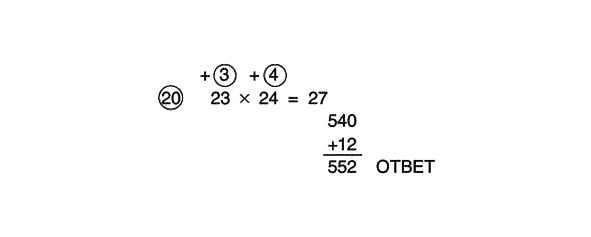
Atbilžu pārbaude
Pielietosim to, ko uzzinājām 4. nodaļā, lai pārbaudītu, vai esam saņēmuši pareizo atbildi:

Aizstāšanas skaitļi 23 un 24 ir attiecīgi 5 un 6.
5 x 6 = 30
3 +0 = 3
3 ir mūsu kontroles numurs.
Sākotnējās atbildes skaitļi (552) ir 3:
5 +5 +2 = 12
1 +2 = 3
Iegūtais skaitlis ir vienāds ar kontroles skaitli, kas nozīmē, ka mēs saņēmām pareizo atbildi.
Mēģināsim atrisināt vēl vienu piemēru:
23 x 31 =
Mēs rakstām 3 un 11 apļos virs 23 un 31, jo mūsu faktori ir attiecīgi par 3 un 11 lielāki par atsauces skaitli 20.
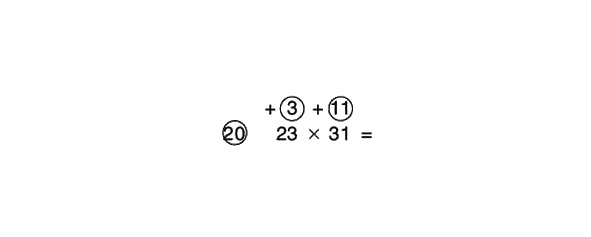
Saskaitot šķērsām, mēs iegūstam 34:
31 +3 = 34 vai 23 +11 = 34
Mēs reizinim iegūto atbildi ar atsauces skaitli 20. Lai to izdarītu, vispirms reiziniet 34 ar 2 un rezultātu ar 10.
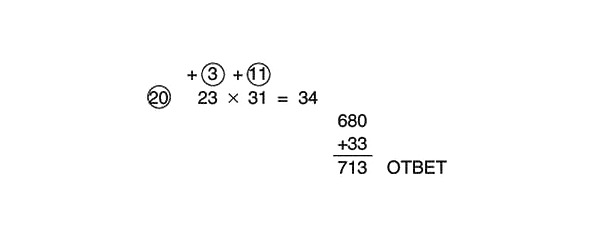
34 x 2 = 68
68 x 10 = 680
Šī ir mūsu pagaidu atbilde. Tagad mēs reizinām skaitļus apļos:
3 x 11 = 33
Pievienosim 33 ar 680:
680 +33 = 713
Pilnībā atrisinātais piemērs izskatās šādi:
Atbildi pārbaudām, izmetot devītniekus.

Sareizināsim aizstāšanas skaitļus un pēc tam summēsim atbildes ciparus:
Tas atbilst mūsu kontroles numuram, tāpēc 713 var uzskatīt par pareizo atbildi.
Šeit ir daži piemēri, kas jums tiek piedāvāti jūsu paša lēmuma pieņemšanai. Kad esat pabeidzis, pārbaudiet savas atbildes, metot devītniekus.
a) 21 x 26 = ___; b) 24 x 24 = ___; c) 23 x 23 = ___; d) 23 x 27 = ___; e) 21 x 36 = ___; e) 26 x 24 = ___
Jums vajadzētu būt iespējai atrisināt šos piemērus savā galvā. Tas nav grūti ar nelielu praksi.
Skaitļus, kas mazāki par 20, reizinot
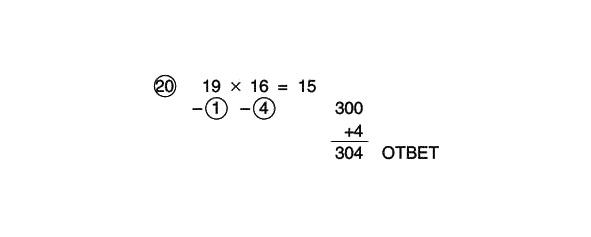
Kā ir ar skaitļu reizināšanu, kas ir mazāki par 20? Ja tie (vai vismaz viens no tiem) ir lielāks par 15, bet mazāks par 20, kā atsauces numuru varat izmantot 20. Atrisināsim piemēru:
Izmantojot 20 kā atsauces numuru, mēs iegūstam:
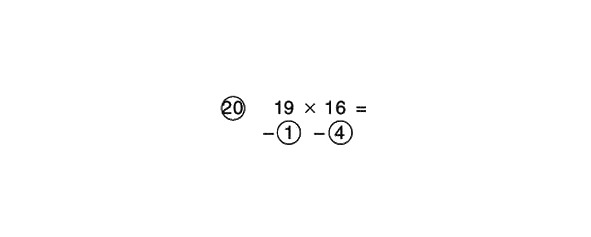
Atņemt šķērsām:
16 – 1 = 15 vai 19 – 4 = 15
Reiziniet ar 20:
15 x 2 = 30
30 x 10 = 300
300 ir mūsu starpposma atbilde.
Tagad sareizināsim apļos esošos skaitļus un pievienosim rezultātu starpatbildei:
1 x 4 = 4
300 +4 = 304
Pilnībā atrisināts piemērs izskatās šādi:
Mēģināsim atrisināt to pašu piemēru, šoreiz izmantojot 10 kā atsauces numuru:
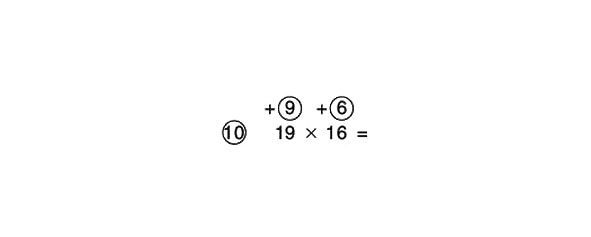
Saskaitīsim šķērsām un pēc tam reizinim rezultātu ar 10, iegūstot starpatbildi:
19 +6 = 25
10 x 25 = 250
Sareizināsim skaitļus apļos un rezultātu pievienosim starpatbildei:
9 x 6 = 54
250 +54 = 304
Pilnībā atrisinātais piemērs izskatās šādi:
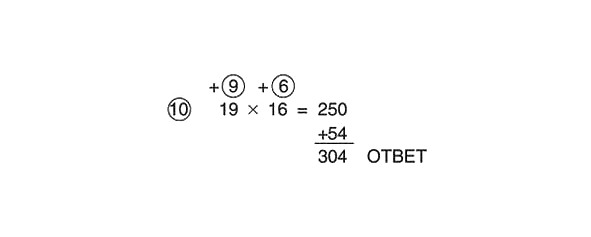
Tas apstiprina iepriekš iegūto rezultātu.
Nav lielas atšķirības starp diviem izmantotajiem atsauces numuriem. Tas ir personīgās izvēles jautājums. Vienkārši izvēlieties atsauces numuru, ar kuru jums ir vieglāk strādāt.
Skaitļi, kas ir lielāki un mazāki par 20
Trešais gadījums ir, kad viens skaitlis ir lielāks, bet otrs ir mazāks par 20. Piemēram:
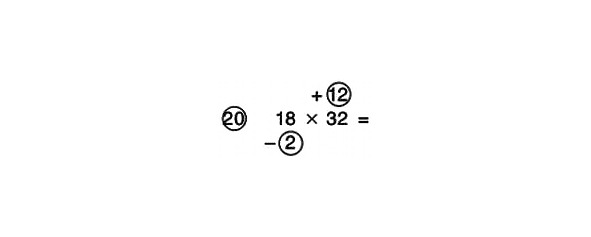
Varat pievienot 18 un 12 vai atņemt 2 no 32 un pēc tam rezultātu reizināt ar atsauces skaitli:
32 – 2 = 30
30 x 20 = 600
Tagad mēs reizinām skaitļus apļos:
2 x 12 = 24
Mēs faktiski reizinām mīnus 2 un 12, tāpēc atbilde ir -24.
600–24 = 576
Risinājuma piemērs izskatās šādi:
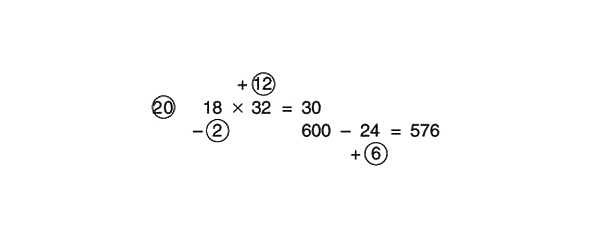
(Lai atņemtu 24, vispirms atņemiet 30 un pēc tam pievienojiet 6.)
Pārbaudīsim atbildi, izmetot devītniekus:
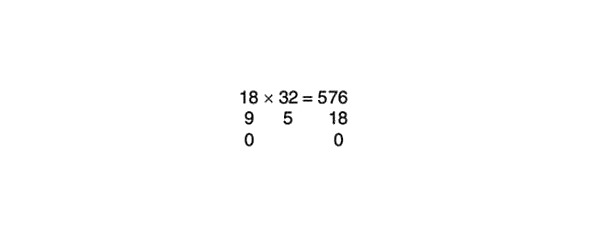
Produkts 0 x 5 ir 0, tātad atbilde ir pareiza.
Reizinot vēl lielākus skaitļus
Iepriekšējā sadaļā mēs runājām par skaitļu pāru reizināšanas metodi līdz 30 x 30. Ko darīt, ja jums ir jāreizina vēl lielāka izmēra skaitļi? Šajā gadījumā kā atsauces skaitli varat izmantot 50. Reizināt ar to ir vienkārši, jo 50 ir puse no 100 vai 100 dalīts ar 2. Tātad, lai reizinātu ar 50, vispirms var reizināt skaitli ar 100 un pēc tam dalīt rezultātu. ar 2.
Izmēģināsim to ar piemēru:
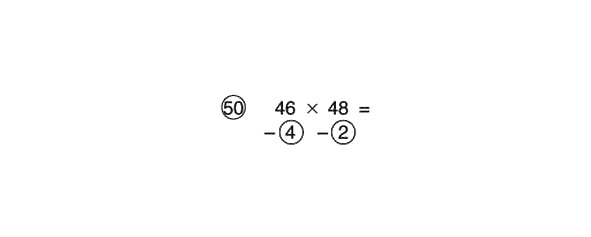
Atņemt šķērsām:
46 – 2 = 44 vai 48 – 4 = 44
Reiziniet 44 ar 100:
44 x 100 = 4400
Mēs sakām sev šādi: «44 uz 100 ir vienāds ar 4400.» Tagad mēs ņemam pusi, kas ir līdzvērtīga 44 reizināšanai ar 50, un mēs iegūstam 2200.
4400: 2 = 2200
Tagad sareizināsim skaitļus apļos un saskaitīsim rezultātu ar 2200:
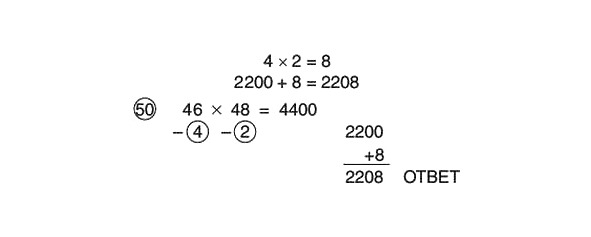
Kas var būt vienkāršāks? Apskatīsim citu piemēru:
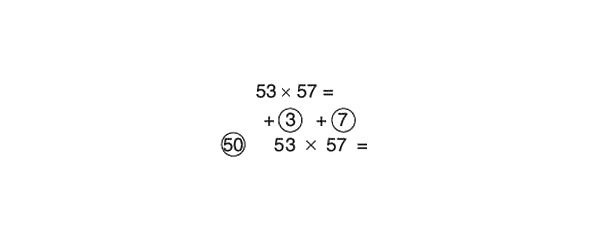
Mēs saskaitām šķērsām, pēc tam reiziniet rezultātu ar atsauces skaitli (reiziniet ar 100 un pēc tam dalām ar 2):
57 +3 = 60
60 x 100 = 6000
6000: 2 = 3000
Reiziniet skaitļus apļos un pievienojiet rezultātu 3000:
3 x 7 = 21
3000 +21 = 3021
Pilnībā atrisinātais piemērs tagad izskatās šādi:
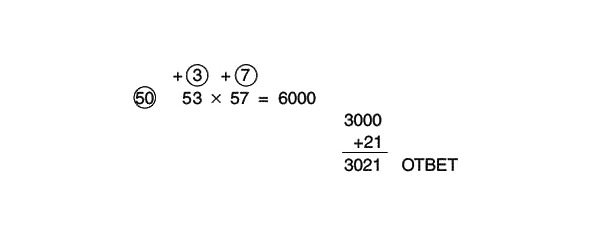
Atrisināsim šādu piemēru:
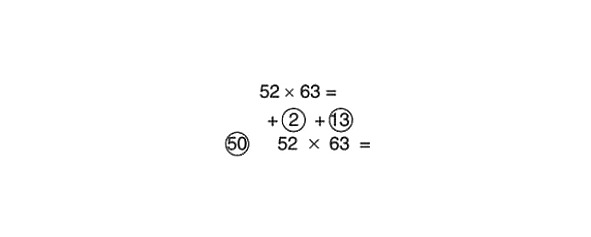
Mēs saskaitām šķērsām un reizinim rezultātu ar atsauces skaitli (vispirms reiziniet ar 100 un pēc tam daliet rezultātu ar 2):
63 +2 = 65
65 x 100 = 6500
Tagad mums ir jādala ar 2.
Nekādu problēmu! Mēs sakām sev: «Puse no sešiem tūkstošiem ir trīs tūkstoši. Puse no piecsimt ir divi simti piecdesmit. Kopā ir trīs tūkstoši divi simti piecdesmit.
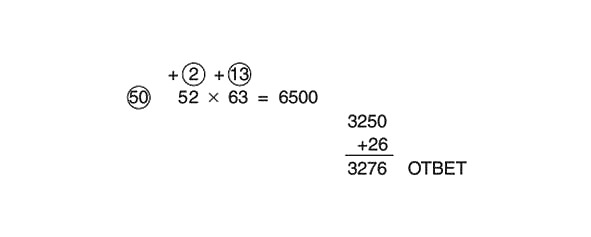
Tagad reizināsim skaitļus apļos:
2 x 13 = 26
Pievienojot 26 starprezultātam 3250, mēs iegūstam 3276. Pilnībā atrisinātais piemērs tagad izskatās šādi:
Pārbaudīsim atbildes pareizību, izmetot devītniekus:

6 plus 3 koeficientā 63 ir vienāds ar 9, kas ir izsvītrots, atstājot aiz 0.
Atbilde ir 3 +6 = 9 un 2 +7 = 9, tas ir, visi skaitļi ir izsvītroti. 7 reizes 0 ir vienāds ar 0, tāpēc atbilde ir pareiza.
Es piedāvāju vairākus piemērus jūsu risinājumam. Centieties savā galvā atrisināt pēc iespējas vairāk piemēru.
a) 46 x 42 = ___; b) 47 x 49 = ___; c) 46 x 47 = ___; d) 44 x 44 = ___; e) 51 x 55 = ___; e) 54 x 56 = ___; g) 51 x 68 = ___; h) 51 x 72 = ___
Atbildes:
a) 1932. gads; b) 2303; c) 2162; d) 1936. gads; e) 2805; f) 3024; g) 3468; h) 3672
Kā jūs tikāt galā ar uzdevumu? Ja iepriekš esi pietiekami trenējies, tev nevajadzētu rasties problēmām to risināšanā savā galvā. Pārbaudiet savas atbildes, izvelkot deviņus.
Divkāršošana un samazināšana uz pusi
Lai kā atsauces skaitļus izmantotu 20 un 50, jums ir jāspēj viegli dubultot un samazināt skaitļus uz pusi.
Reizēm, kad, piemēram, mums ir jādala uz pusēm divciparu skaitlis, kura desmitnieku skaitlis ir nepāra, atbilde pati par sevi neliecina. Piemēram:
78: 2 =
Lai uz pusi samazinātu 78, varat dalīt 70 ar 2, pēc tam 8 un pēc tam pievienot rezultātus. Bet ir vēl vienkāršāks veids.
78 = 80—2. Puse no 80 – 2 ir vienāda ar 40 – 1. Šī ir atbilde:
40 – 1 = 39
Lai dubultotu 38, garīgi iedomājieties šo skaitli kā 40 – 2. Divkāršot vērtību, tā būs 80 – 4, tas ir, 76.
Mēģiniet pats atrisināt šādus piemērus:
a) 38 x 2 = ___; b) 29 x 2 = ___; c) 59 x 2 = ___; d) 68 x 2 = ___; e) 39 x 2 = ___; e) 47 x 2 =
Atbildes:
a) 76; b) 58; c) 118; d) 136; e) 78; e) 94
Tagad atrisiniet šos piemērus:
a) 38: 2 = ___; b) 56: 2 = ___; c) 78: 2 = ___; d) 94: 2 = ___; e) 34: 2 = ___; e) 58: 2 = ___; g) 18: 2 = ___; h) 76: 2 = ___
Atbildes:
a) 19; b) 28; c) 39; d) 47; e) 17; f) 29; g) 9 h) 38
To pašu pieeju var izmantot, lai reizinātu un dalītu diezgan lielus skaitļus ar 3 un 4. Piemēram:
19 x 3 = (20 – 1) x 3 = 60 – 3 = 57
38 x 4 = (40 – 2) x 4 = 160 – 8 = 152
Numuri 200 un 500 kā atsauces numuri
Ja reizinātie skaitļi ir tuvu 200 vai 500, aprēķini nav īpaši sarežģīti, jo gan 200, gan 500 ir viegli izmantot kā atsauces skaitļus.
Kā, piemēram, atrodam produktu 216 x 216? Ja kā atsauci izmantojat 200, piemēru var viegli atrisināt, tostarp jūsu galvā:
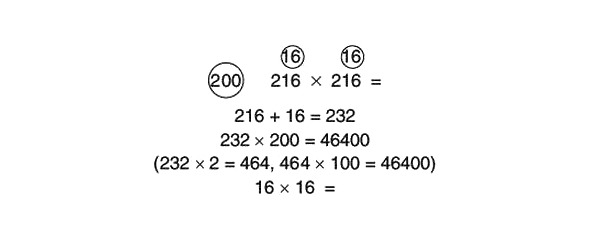
Mēs aprēķinām 16 x 16, izmantojot 10 kā atsauces skaitli.
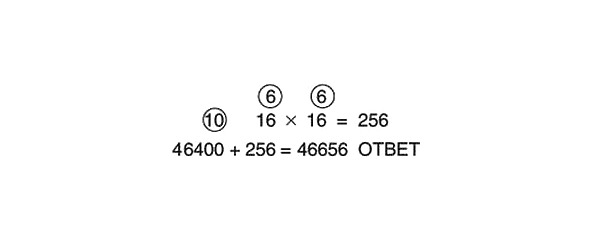
Kā ar 512x512?
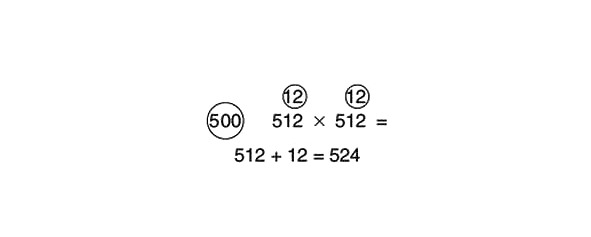
512 x 500 ir vienāds ar 524 x 1000 dalīts ar 2.
524 x 1000 = 524 000 jeb 524 tūkst.
Puse no 524 tūkstošiem ir vienāda ar 262 tūkstošiem.
Lai 524 tūkstošus sadalītu uz pusēm, tos var sadalīt uz 500 tūkstošiem un 24 tūkstošiem. Pusi no abiem skaitļiem ir viegli aprēķināt galvā. Puse no 500 tūkstošiem ir vienāda ar 250 tūkstošiem. Puse no 24 tūkstošiem ir vienāda ar 12 tūkstošiem. 250 tūkstoši plus 12 tūkstoši dod 262 tūkstošus.
Tagad reizināsim skaitļus apļos:
12 x 12 = 144
262000 +144 = 262144 ATBILDE
Mazāku skaitļu reizināšana
Mēģināsim atrast produktu 6 x 4:
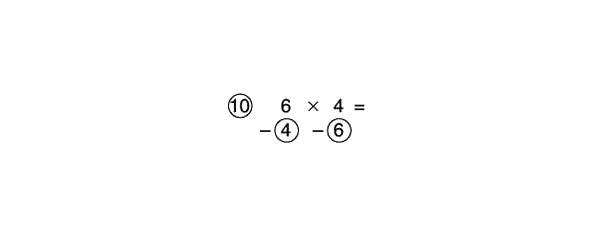
Kā atsauces skaitli izmantojam 10. Zem faktoriem ievelkam apļus, jo gan 6, gan 4 ir mazāki par 10. Atņem šķērsām:
6–6 = 0 vai 4–4 = 0
Tagad reizināsim skaitļus apļos:
4 x 6 =
Mēs esam atgriezušies pie sākotnējās problēmas (6 x 4). Šķiet, ka metode mums nekādi nepalīdzēja. Vai ir iespējams panākt, lai tas darbotos arī šādos gadījumos? Tas ir iespējams, taču šim nolūkam ir jāizmanto cits atsauces numurs. Mēģināsim pieņemt skaitli 5 kā tādu. 5 ir 10 dalīts ar 2, vai puse no 10. Visvieglāk reizināt ar 5 var, reizinot ar 10 un rezultātu dalot ar 2.
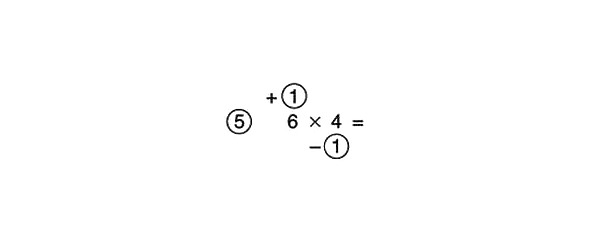
6 ir lielāks par 5, tāpēc mēs tam uzzīmējam apli. 4 ir mazāks par 5, tāpēc aplis tam tiek novilkts zemāk. 6 ir vairāk nekā 5 reizes 1, tāpat kā 4 ir mazāks par 5 reizi 1, tāpēc katrā aplī ierakstām 1.
Pievienojiet 4 un 1 šķērsām vai atņemiet 1 no 6:
6–1 = 5 vai 4 +1 = 5
Mēs reizinām 5 ar atsauces numuru, kas arī ir 5.
Lai to izdarītu, mēs vispirms reizinām ar 10, kas dod mums 50, un pēc tam rezultātu sadalām ar 2, iegūstot 25. Tagad mēs reizinām skaitļus apļos:
1 x -1 = -1
Tā kā rezultāts ir negatīvs skaitlis, mēs to atņemam no starpatbildes, nevis pievienojam tai:
25 – 1 = 24
Tādējādi:
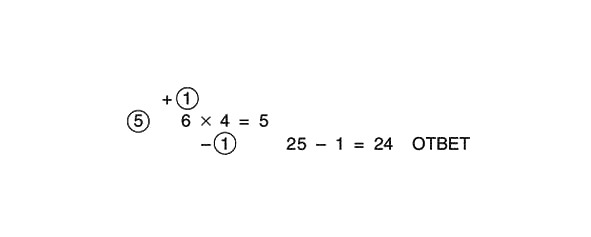
Tas ir ļoti garš un apgrūtinošs nelielu skaitļu reizināšanas veids, taču tas parāda, ka ar nelielu atjautību metodi var panākt, lai tā darbotos visos gadījumos. Turklāt šādas pieejas palīdz attīstīt sānu domāšanas spēju, kas ir ļoti svarīga matemātiķim un vispār jebkuram cilvēkam, ja viņš vēlas gūt panākumus dzīvē.
Apskatīsim vēl vienu piemēru, pat ja jūs labi zināt reizināšanas tabulu:

Atņemt šķērsām:
4—1 = 3
Sareizināsim rezultātu ar atsauces numuru:
3 x 10 = 30
30: 2 = 15
Tagad reizināsim skaitļus apļos:
1 x 1 = 1
Pievienosim šo rezultātu starpatbildei:
15 +1 = 16
Tādējādi:
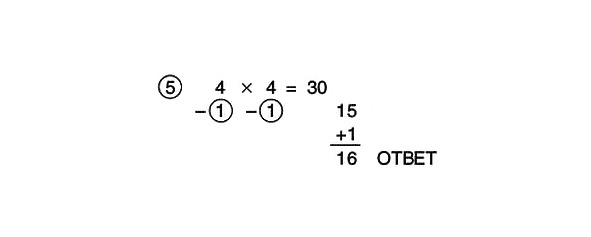
Mēģiniet pats atrisināt šādus piemērus:
a) 3 x 4 = __; b) 3 x 3 = __; c) 6 x 6 = __; d) 3 x 6 = __; e) 3 x 7 = __; e) 4 x 7 = __
Atbildes:
a) 12; b) 9; c) 36; d) 18; e) 21; e) 28
Esmu pārliecināts, ka šo piemēru risināšana jums nesagādāja ne mazāko problēmu. Es nedomāju, ka tas ir labākais veids, kā apgūt reizināšanas tabulas maziem skaitļiem. Manuprāt, visvieglāk ir to iemācīties. Bet daži cilvēki vēlas uzzināt, kā reizināt mazus skaitļus, izmantojot šo metodi, lai pārbaudītu tās daudzpusību. Citiem tas var patikt, jo viņi būs pārliecināti, ka pat tad, ja viņi aizmirst savas laika tabulas, ir vienkāršs veids, kā aprēķināt nepieciešamo produktu. Turklāt, pat ja jūs zināt savas reizināšanas tabulas no galvas, dažreiz var būt noderīgi un jautri spēlēt šādas spēles un eksperimentēt ar skaitļiem.
Reiziniet ar 5
Kā redzējām, lai reizinātu ar 5, vispirms var reizināt ar 10 un pēc tam rezultātu dalīt uz pusi. 5 ir vienāds ar pusi no 10. Lai reizinātu 6 ar 5, varat reizināt 6 ar 10, kas dod 60, un pēc tam rezultātu dalīt uz pusēm, iegūstot 30.
Izmēģiniet to pats:
a) 8 x 5 = __; b) 4 x 5 = __; c) 2 x 5 = __; d) 6 x 5 = __
Atbildes:
a) 40; b) 20; pulksten 10; d) 30
Bet ko darīt, ja desmitnieku skaits ir nepāra. Reiziniet 7 ar 5:
7 x 10 = 70
Ja jums ir grūti uzreiz sadalīt 70 uz pusēm, iedomājieties to kā summu: 60 +10. Tās puse ir 30 +5, kas ir 35.
Apskatīsim citu piemēru:
9 x 5 =
9 reiz 10 ir vienāds ar 90. 90 var uzrakstīt kā 80 +10. Puse no 80 +10 ir 40 +5, tātad atbilde ir 45. Atrisiniet paši:
a) 3 x 5 = __; b) 5 x 5 = __; c) 9 x 5 = __; d) 7 x 5 = __;
Atbildes:
a) 15; b) 25; c) 45; d) 35
Šis ir vienkāršs veids, kā uzzināt skaitļa 5 laika tabulas. Tas darbojas, ja skaitļi tiek reizināti ar 5. Piemēram:
14 x 5 =
14 x 10 = 140, un 140 dalīts ar 2, iegūst 70.
Tāpat:
23 x 5 =
23 x 10 = 230
230 = 220 +10
Puse no 220 +10 ir 110 +5
110 +5 = 115
Visus šos aprēķinus pēc nelielas prakses var izdarīt daudz ātrāk savā galvā.







