
Д. В. Ушаков
Психология интеллекта и одаренности
Построение формальной модели
Изложенные положения модели дают основания перейти к ее формализации[7]. Эта формализация имеет двоякое значение. Во-первых, в практическом плане она открывает путь к количественным оценкам и тем самым сообщает модели предсказательные возможности. В частности, она позволяет дать экономические оценки различным сценариям работы с одаренными детьми. Во-вторых, в исследовательском плане формализация ускоряет процесс совершенствования теории, поскольку позволяет формулировать точные предсказания, соотнесение которых с действительностью выявляет нестыковки в теории и заставляет вносить в последнюю изменения. В то же время любая формализация связана со схематизацией, отбрасыванием части «пышно зеленеющего древа жизни» в пользу сухой теории. В особой степени это касается ее начальных этапов, когда закладываются принципы схематизации для той или иной области. Поэтому представляется, что оптимальным путем сегодня является сочетание двух подходов – номотетического, стремящегося к созданию абстрактных моделей, и идеографического, сохраняющего богатство живого представления о человеческой личности.
Вначале необходимо ввести функции, отображающие способности на компетентности и компетентности – на экономические достижения. Первая описывает, каким образом у групп людей, включенных в экономический процесс, на основе способностей формируются компетентности, и фактически является показателем работы образовательной системы страны. Функция, отображающая компетентности на экономические достижения, характеризует экономическую систему государства, а именно востребованность в ней высококомпетентных специалистов.
Для наших целей удобно сразу использовать одну функцию, являющуюся композицией двух перечисленных, поскольку при этом можно воспользоваться данными Р. Линна, которые приводят в соответствие способности и экономические достижения.
Для удобства последующих расчетов преобразуем оси интеллекта I и экономических показателей D таким образом, чтобы все данные Линна уместились в отрезках [0, 1]. Это достигается за счет следующего преобразования:
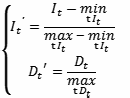
где индекс t обозначает соответствующую страну в данных Линна. Далее будем работать в новых осях, поэтому штрихи учитывать для удобства не будем.
Рассмотрим два варианта аппроксимации: при помощи степенной функции и при помощи показательной функции, которую предлагает Дикерсон (Dickerson, 2006). Мы пойдем по двум путям отдельно, а потом сравним полученные результаты.
Все степенные и показательные функции представим в виде трехпараметрического семейства:
F1(I; k, m, a) = m(I – a)k,
F2(I; k, m, a) = m × k(I – a).
Будем искать соответствующие функции f1(I) и f2(I) методом наименьших квадратов:
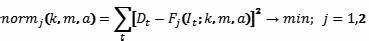
Следует отметить, что данные Линна имеют различную надежность для разных стран. Для большей части стран они основываются на эмпирических исследованиях, охвативших выборки большего или меньшего размера. Однако Линн расширяет свой список путем добавления стран, для которых интеллект оценен косвенно, в частности, путем сопоставления с интеллектом в соседних странах. Таким образом, мы располагаем менее обширным списком стран, для которых оценки интеллекта более надежны, и расширенным списком, для которого, однако, оценки интеллекта менее надежны. Расчеты были проведены отдельно по полному списку и – по сокращенному. В последний были включены страны, где данные по интеллекту были получены на выборке не менее 400 человек.
Линн сопоставляет свои данные по интеллекту с показателями ВВП за 2002 г. Более на дежно, однако, брать данные по ВВП не за один год, а за несколько, поскольку этим снижается влияние краткосрочных экономических факторов. Соответственно мы осуществили расчеты как на основании приводимых Линном данных за 2002 г., так и на основании усредненных показателей за 2002, 2006 и 2007 гг. Данные за 2006 г. были взяты с сайта Международной организации здравоохранения (World Health Organization), а за 2007 г. – с сайта Всемирного банка (World Bank). Данные за 2006 и 2007 гг. удалось получить не по всем странам, представленным в списках Линна, поэтому краткий список сократился на 6 стран, а расширенный – на 10. Из всех выборок исключены Китай и Экваториальная Гвинея.
Результат решения задачи для разных вариантов данных суммирует таблица 1.4.
На основании данных, представленных в таблице, можно заключить, что наиболее точно связь национального интеллекта и доходов на душу населения аппроксимирует степенная функция с показателями, варьируемыми от 2,08 до 2,6 для разных вариантов данных. Однако если взять показатель степени, равный 2, то полученная квадратичная функция, как видно из таблицы 1.4, аппроксимирует данные лишь чуть хуже, чем степенная с оптимально определенным показателем степени, и примерно так же (а для данных с достоверными коэффициентами интеллекта даже лучше), как это делает показательная функция. Стоит отметить, что точность аппроксимации в случае усредненных доходов на душу населения по трем годам оказывается выше, чем для одного года.
Далее мы проведем расчеты на основании двух моделей – квадратичной и степенной, а затем сравним сходство вытекающих из них оценок. Эти модели являются наиболее контрастными, поскольку степенная предполагает наиболее быстрый рост функции при возрастании аргумента, а квадратичная – наиболее медленный. Следовательно, степенная модель будет давать наиболее высокие оценки экономическому вкладу одаренной части населения, а квадратичная – самые низкие. В связи с этим, если оценки, полученные на основании двух моделей, окажутся достаточно близкими, это станет свидетельством высокой стабильности результатов, получаемых на основании предложенного подхода.
Таблица 1.4. Аппроксимация связи национального интеллекта и доходов на душу населения
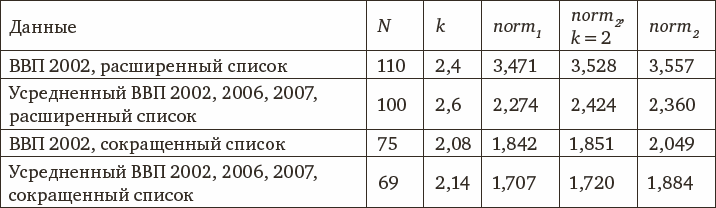
Примечание: N – количество стран, k – полученный в результате решения задачи коэффициент степенной функции. В остальных трех столбцах отображены полученные нормы соответственно для степенной модели, для степенной модели с заданной степенью равной 2 и для показательной модели.
Вклад групп населения с различным интеллектом в экономику страны
Приведенные выше закономерности являются стохастическими, и возникает вопрос о причинах отклонений отдельных стран от аппроксимирующей зависимости. В контексте понимания экономики как решения задач ответ на этот вопрос включает несколько пунктов. Во-первых, для реализации интеллектуального потенциала людей необходимо, чтобы экономика в достаточном количестве предоставляла такие рабочие места, где необходим высокий уровень интеллектуальных компетентностей или же повышение их уровня приводит к повышению результата. Если в экономике минимальна потребность в квалифицированном труде, то и высокий интеллект граждан ничего не даст. Во-вторых, необходимо, чтобы существующие в стране рабочие места, связанные с решением наиболее сложных задач, приносили экономическую отдачу. Это условие также не всегда выполняется. В стране могут существовать рабочие места, например, в науке, которые требуют очень высокого интеллекта и компетентностей, однако наука не имеет в этой стране такого внедрения в экономику, которое позволило бы существенно увеличить национальный доход. Наконец, еще одним необходимым условием является наличие такой системы образования в широком смысле слова, которое позволяет формировать достойные компетентности на базе высоких способностей.
Страны, в которых высокий интеллект дополняется тремя перечисленными условиями, имеют высокие экономические достижения, но недостаточность хотя бы в одном звене из трех существенно снижает возможности реализации интеллектуального потенциала населения.
Проведенный анализ важен для перехода от интернационального уровня к национальному. Может ли быть перенесена полученная на наднациональном уровне зависимость интеллекта и ВВП на уровень внутри страны? Если вклад групп с различным уровнем интеллекта остается пропорциональным во всех странах, тогда закономерность допускает перенос. Если же снижение степени реализации интеллекта связано с понижением вклада наиболее интеллектуальных групп, то закономерности будут различными для стран, лежащих выше и ниже аппроксимирующей кривой.
Приняв допущение о пропорциональности вкладов, легко оценить, как вклады различных групп, так и отдачу, которую можно получить от работы с наиболее одаренными представителями населения. Однако при этом необходимо помнить, что условием этих подсчетов является указанное допущение. Если это допущение неверно, то для стран с высоким уровнем реализации интеллектуального потенциала оценки вклада наиболее интеллектуальных групп окажутся заниженными, а для стран с низким уровнем – завышенными. Это допущение в дальнейшем может быть проверено эмпирически на основе экономических данных по разным странам.
На основе принятой предпосылки оценим теперь вклад в экономические результаты страны групп населения с различным уровнем способностей. На первый взгляд может показаться, что функция, связывающая интеллект гомогенных в интеллектуальном отношении групп с их продуктивностью, и функция, связывающая средний интеллект страны с ее экономическими результатами, совпадают. В действительности, однако, это не так, причем одна функция может быть выведена из другой. Различим частный интеллект i, под которым подразумевается интеллект групп людей внутри страны, и интеллект I страны в целом. Под i может пониматься в том числе интеллект отдельного человека – гражданина той или иной страны. Мы будем полагать, что распределение интеллекта i подчинено нормальному закону с одинаковой дисперсией для всех стран.
Рассмотрим вначале квадратичную модель. Отметим, что нулем интеллекта имеет смысл считать значение, равное 60. В этом случае убирается коэффициент сдвига в степенной функции, и, кроме того, такое значение говорит о том, что для интеллекта ниже 60 отсутствуют производимые продукты, влияющие на экономические показатели. Это предположение с психологической точки зрения правдоподобно, поскольку значения коэффициента интеллекта, меньшие 60 баллов, соответствуют достаточно глубокой олигофрении.
Таким образом, мы «избавились» от коэффициента сдвига в степенной функции. Заметим, что коэффициент масштаба для наших целей также не является существенным, поскольку нас будут интересовать не абсолютные значения, а относительные.
Итак, мы можем представить аппроксимирующую функцию в виде:
F1(I) = I2.
Будем искать вклад в экономические достижения также в виде f1(i) = ik. Это объясняется двумя причинами. Во-первых, зависимость экономических достижений стран от интеллекта не зависит от численности населения той или иной страны, во-вторых, вклад отдельного человека в экономику в целом не ограничивается его личными достижениями, а в совокупности влияет на многие сферы, напрямую не связанные с его деятельностью.
В пересчете на используемую шкалу дисперсия интеллекта, составляющая по определению 15 баллов шкалы IQ, равна 0,3. Для значений меньше 0, что соответствуют данным Линна для интеллекта меньше 60, будем полагать, что вклад в экономические достижения равен нулю. На значения интеллекта, больше 1, продолжим естественным образом нашу функцию.
Тогда для отдельной страны со средним интеллектом можем рассчитать экономические достижения по формуле:

Нам требуется, чтобы общие экономические достижения страны были представимы функцией F1(I) = I2.
Значит, должно выполняться условие:
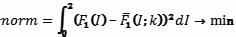
где 2 соответствует максимальному интеллекту.
Получим, что k = 2. Итак, f1() = i2.
Оценка асимметрии распределения достижений среди населения
На основании произведенных выкладок можно оценить вклад в экономику, который вносят наиболее и наименее одаренные группы населения, что позволяет сравнить количественные оценки модели с упоминавшимися выше распределением Парето и законом Прайса. Еще раз необходимо подчеркнуть, что эта оценка условна, поскольку экономический эффект в современном мире достигается в результате совместных действий множества людей и результат отдельного действия можно оценить лишь в абстракции. Изложенное выше представление о деятельности как включающей решение совокупности задач различной сложности ведет к оценке вклада в решение отдельной задачи в терминах повышения общего уровня результата деятельности.
Для России I= 0,74, i~N(0,74, 0,32).
Плотность распределения равна:

Мы можем посчитать вклад в экономику 20 % наиболее одаренного населения России.
Найдя 80 % квантиль нашего распределения
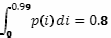
получим продуктивность для нижних 80 % населения
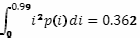
и продуктивность для 20 % наиболее способного населения
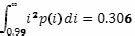
Таким образом, вклад 20 % наиболее одаренного населения в экономические достижения России составляет 43 %. Поскольку в излагаемой модели заложено, что способности людей не выражаются однозначно в их продуктивности, то естественно, что продуктивность 20 % наиболее способных людей существенно ниже, чем продуктивность 20 % наиболее продуктивных. Рассогласование между этими двумя цифрами показывает запас нереализованных возможностей, который заложен в интеллектуальном потенциале страны, но не востребован ею.
Формализация экономического эффекта образовательных программ для наиболее одаренной части населения
Теперь заложены необходимые основания, чтобы оценить экономическую эффективность программ, направленных на образование наиболее одаренной части населения. Теоретически можно допустить два пути действия этих программ.
Во-первых, можно пытаться достичь повышения способностей участников, т. е. условно сдвинуть на графике вправо наиболее способную часть населения. Хотя повышение способностей очень заманчиво, и многие программы декларируют его в качестве своей цели, все же сегодня не существует убедительных данных о том, что эта цель реально достижима. Независимая оценка так называемых программ когнитивного обучения (cognitive education), направленных на повышение когнитивного уровня людей, не выявляет того эффекта, на который рассчитывают их разработчики (Loarer et al., 1995; Shayer, 1987).
Сказанное не означает, что интеллект в принципе не поддается развитию. Психогенетические исследования показывают, что, хотя интеллект и является в значительной степени генетически обусловленным свойством, все же от 20 до 50 % его дисперсии определяет окружающая среда (Егорова, 1995; Bouchard, 1997). Однако сегодня психологи еще недостаточно владеют средствами целенаправленного воздействия на интеллект, поэтому такой вариант в модели рассматриваться не будет. Понятно, что принятие этого варианта повысило бы итоговые оценки эффективности программ.
Во-вторых, программы работы с одаренными могут быть нацелены на увеличение возможностей реализации их потенциала при неизменном уровне интеллекта. В модели это может быть представлено в виде смещения в сторону более высоких значений продуктивности наиболее способной части населения.
Этот вариант является более реалистичным, поскольку хорошо поставленное образование одаренных, даже не повышая их способности, тем не менее позволяет вступить на путь устойчивой профессионализации и добиться на нем успехов.
Если увеличить эффективность 5 % наиболее одаренного населения на 50 %, то увеличение экономических достижений может быть посчитано следующим образом.
Найдем 95 % квантиль нашего распределения
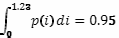
Тогда:

Таким образом, можем сказать, что если увеличить эффективность 5 % наиболее одаренного населения на 50 %, то увеличение экономических достижений составит 7,4 % для всей страны в целом.
Количественная оценка экономического эффекта программ развития одаренных детей произведена для различных сценариев по охвату населения и по эффективности программ в плане реализации потенциала одаренных людей. Расчеты осуществлены для охвата от 0 до 5 % населения и для трех вариантов образовательной эффективности. Результаты приведены на рисунке 1.4.
Насколько велики полученные численные значения эффекта? Эти цифры представляются очень существенными и безусловно превышают все разумные расходы на программы образования одаренных детей и даже на все образование страны в целом. Конечно, они не настолько велики, чтобы ликвидировать отставание России от ведущих стран в плане экономического развития, однако в абсолютном выражении составляют десятки миллиардов рублей в год.
Очевидно, что вторая производная функции прироста ВВП при увеличении охвата населения является отрицательной, т. е. при увеличении охвата отдача от программ в пересчете на душу населения снижается. Это означает, что наибольшего экономического эффекта следует ожидать от работы с достаточно узкой прослойкой интеллектуальной элиты. Тем не менее при пятипроцентном охвате экономическая эффективность программ продолжает оставаться очень высокой.
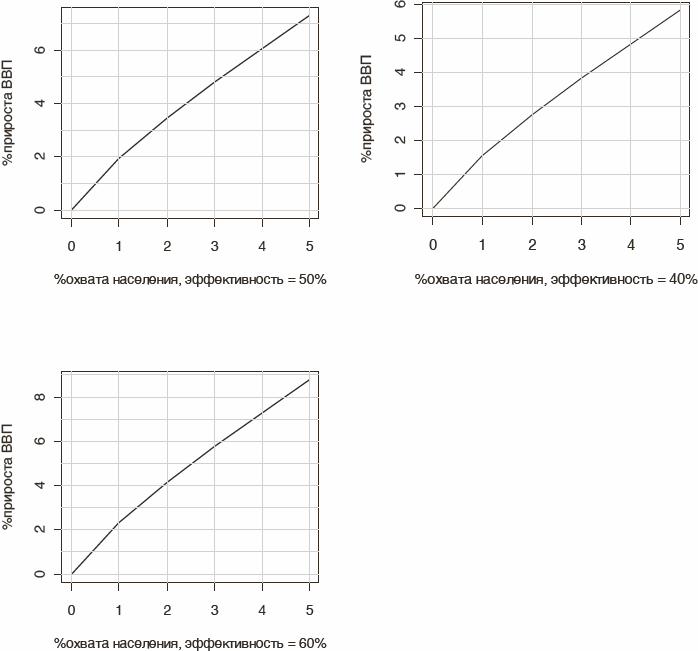
Рис. 1.4. Количественная оценка экономической эффективности образовательных программ для наиболее одаренной части населения
Модель на основе степенной функции
Коэффициент сдвига для показательной функции есть коэффициент масштаба, поэтому аппроксимирующую функцию мы можем представить в виде:
F2(I) = 11I.
Будем искать вклад в экономические достижения также в виде f2(i) = ki. Будем исходить из условия нормальности распределения интеллекта внутри страны с одинаковой дисперсией внутри всех стран равной 15. На приведенной шкале это будет равно 0,34.
Для отдельной страны со средним интеллектом I можем рассчитать экономические достижения:

Нам требуется, чтобы общие экономические достижения страны бы ли представимы функцией F2(I) = 11I.
Значит, должно выполняться условие:

Получим, что k = 10. Итак, f2(i) = 10i.
Проведя оценку асимметрии распределения достижений населения, получим, что вклад 20 % наиболее одаренного населения в экономические достижения России составляет 47 %. Модель на основе квадратичной функции, как было показано выше, дает оценку этого параметра в 43 %, поэтому можно констатировать совпадение двух моделей с погрешностью менее 10 %.
Проведя оценку экономической эффективности программ, получим, что если увеличить эффективность 5 % наиболее одаренного населения на 50 %, то увеличение экономических достижений составит 9 % для всей страны в целом. Результат также достаточно близок к оценкам, получаемым на основе квадратичной модели.
Следует, однако, напомнить, что в основе полученных оценок лежит допущение пропорциональности вклада групп с различным уровнем интеллекта в экономику различных стран. Это допущение заслуживает в дальнейшем эмпирической проверки.
Интеллект и экономика как решение задач
Парадигма экономики как обмена показала себя очень продуктивной в отношении анализа различных сторон экономической жизни общества. Понимание экономики как решения задач имеет локальную применимость. Возможно, однако, что с ее помощью можно будет подойти к другим сферам действительности, и тогда аппарат психологической теории способностей получит более широкое экономическое применение. Уже сейчас можно наметить поле применения разработанной модели.
Прежде всего модель может стать основой для эмпирических исследований. Одно из направлений этих исследований связано с проверкой предсказаний модели. Выше уже приводился пример такой возможности: проверить предсказание модели об увеличении асимметричности распределения достижений при повышении сложности («творческости») деятельности. Другое направление заключается в оценке реального положения дел с использованием интеллектуального потенциала в экономике различных стран и степени его реализации в образовательной системе. Так, практически важным было бы оценить то, в какой степени различные образовательные формы и структуры (специальные школы для одаренных, летние лагеря, дополнительное образование и пр.) увеличивают вероятность того, что одаренные люди в большей степени реализуют себя в творческих профессиональных достижениях. В сочетании с разработанной моделью такое исследование позволит оценить экономический эффект этих мероприятий и сопоставить его с затратами.
Модель также может расширяться и усложняться путем включения дополнительных переменных, в том числе психологических. Интеллект не является единственным психологическим конструктом, имеющим экономическое значение. Еще в середине прошлого века Мак-Клелландом была показана роль мотивации достижения для развития экономики. Основываясь на идеях М. Вебера о связи духа протестантизма с капиталистическим производством и промышленной революцией, Мак-Клелланд выдвинул предположение, что высокая мотивация достижения у населения побуждает к активной предпринимательской деятельности, которая через реинвестирование прибылей и стимуляцию технических достижений способствует экономическому росту (McClelland, 1961). Для проверки этого предположения он произвел оценку выраженности мотива достижения в различных странах, используя контент-анализ книг для чтения младших школьников. Построенная таким образом оценка мотивации достижения на 1925 г. коррелировала на уровне r = 0,53 с коэффициентом, выявляющим прирост энергопотребления в соответствующих странах в 1950 г.
Более поздние исследования подтвердили экономическое значение мотивации достижения. Было показано, что высокая мотивация достижения, устанавливаемая контент-анализом литературных произведений ушедших эпох (например, греческой лирики и эпиграмм, испанских стихов и романов, английских драм, путевых дневников и баллад), предшествует эпохам экономического подъема, отражающегося в экспорте и импорте товаров (Хекхаузен, 2003). Аналогичные по смыслу результаты были получены в исследовании изменений мотивации достижения в США (выявленной на основе контент-анализа) и числа патентов в этой стране (de Charms, Moeller, 1962).
Данные о влиянии мотивации достижения на экономические успехи находят свое логическое место в представлении экономики как решения задач. Высокая мотивация достижения увеличивает успешность в решении задач. Можно предположить, что для определенного уровня интеллекта мотивация достижения улучшает приобретение компетентностей, а также увеличивает степень реализованности компетентностей в экономически ценных результатах. Эти феномены могут быть эмпирически оценены, а затем соотнесены в рамках разработанной модели с приростом, наблюдаемым в экономике государств в связи с мотивацией достижения.
Более новые работы показали экономическую роль культурных ценностей. Так, Ш. Шварц выделяет три измерения культурных ценностей: независимость/принадлежность, иерархия/равноправие и гармония/мастерство (Schwartz, 2007). Межкультурные сравнения позволили выявить значимые связи выраженности этих ценностей в различных странах с их экономическими, политическими и социальными показателями. Например, независимость коррелирует на уровне r = 0,74–0,76 с валовым национальным продуктом на душу населения, на уровне r = –0,74 (r = –0,61 при контроле валового национального продукта) – с уровнем коррупции. Возможно, эти данные выводят на включение в модель взаимодействия людей, которое определяется такими ценностями, как независимость, и в то же время в свою очередь влияет на успешность решения экономических задач.
Наконец, модель может применяться не только на уровне анализа экономик целых стран, но и на более низком уровне – уровне отдельных предприятий. Очевидно, что работа предприятия также может быть представлена в виде решения задач, компетентность сотрудников в котором влияет на общие показатели эффективности. Таким образом, открывается возможность моделирование и оптимизация деятельности предприятий, имеющих различную структуру сложности задач.







